18.2.2-2菱形(共17张PPT)
文档属性
| 名称 | 18.2.2-2菱形(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 517.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览



文档简介
第十八章 平行四边形
18.2.2 菱形
第2课时
18.2 特殊的平行四边形
课前预习:课本57---58
预习目标:
1、回顾矩形的定义、性质及判定。菱形的定义和性质。
2、探讨菱形有哪些判定方法?并会证明。
3、会灵活运用菱形的判定方法解决问题。
4、说一说本节课的收获。
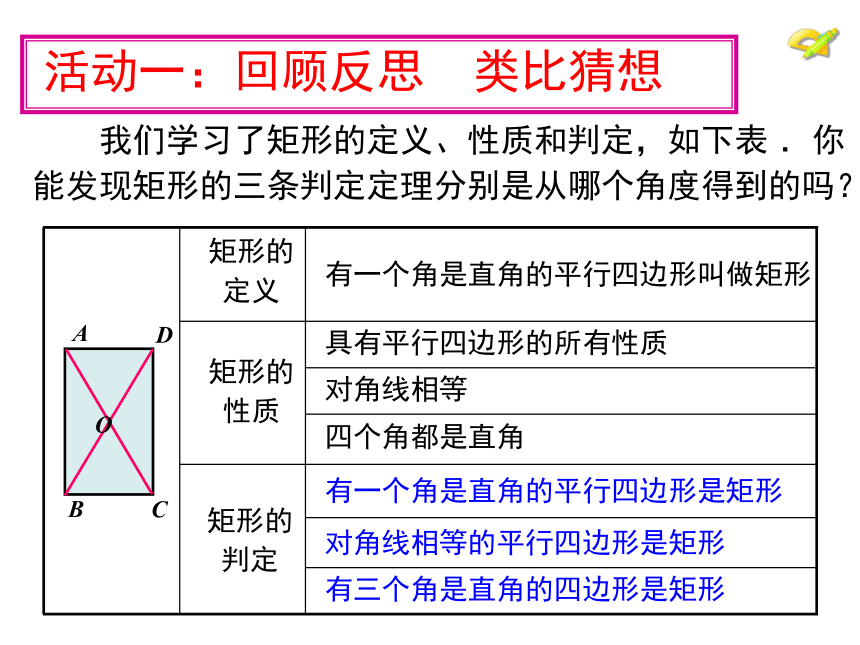
活动一:回顾反思 类比猜想
我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?
矩形的
定义
有一个角是直角的平行四边形叫做矩形
矩形的
性质
具有平行四边形的所有性质
对角线相等
四个角都是直角
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
C
D
A
B
O
矩形的
判定
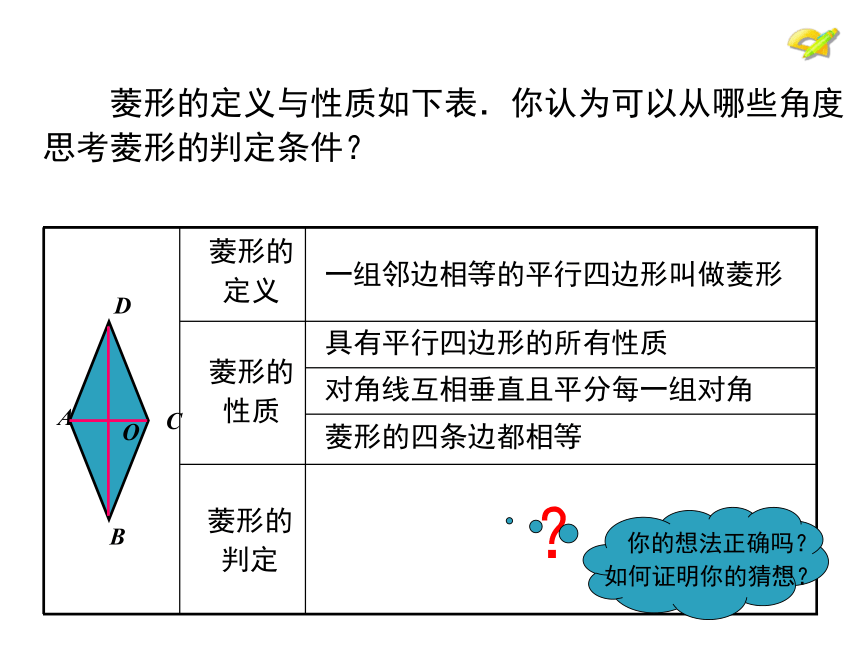
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
?
你的想法正确吗?
如何证明你的猜想?
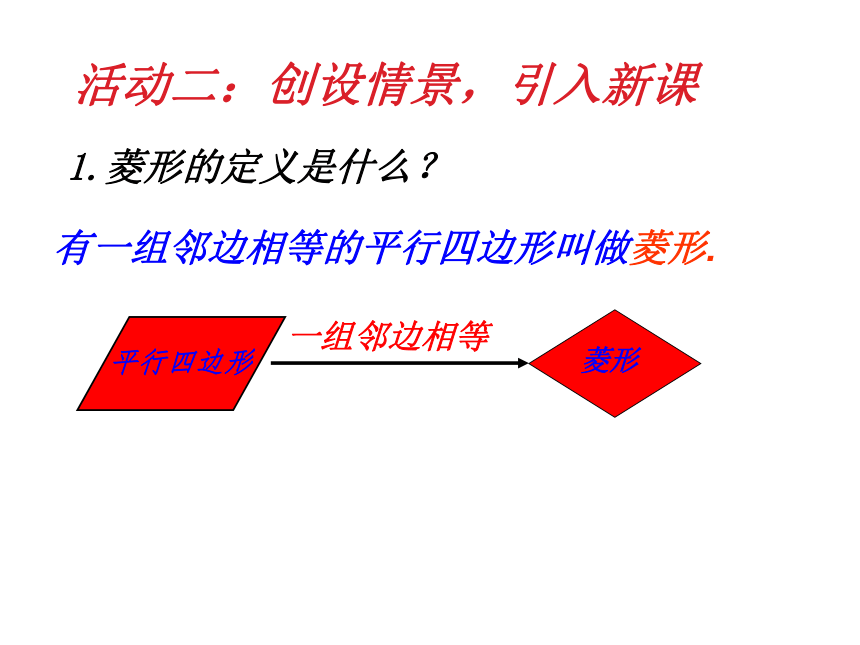
1.菱形的定义是什么?
有一组邻边相等的平行四边形叫做菱形.
一组邻边相等
平行四边形
菱形
活动二:创设情景,引入新课
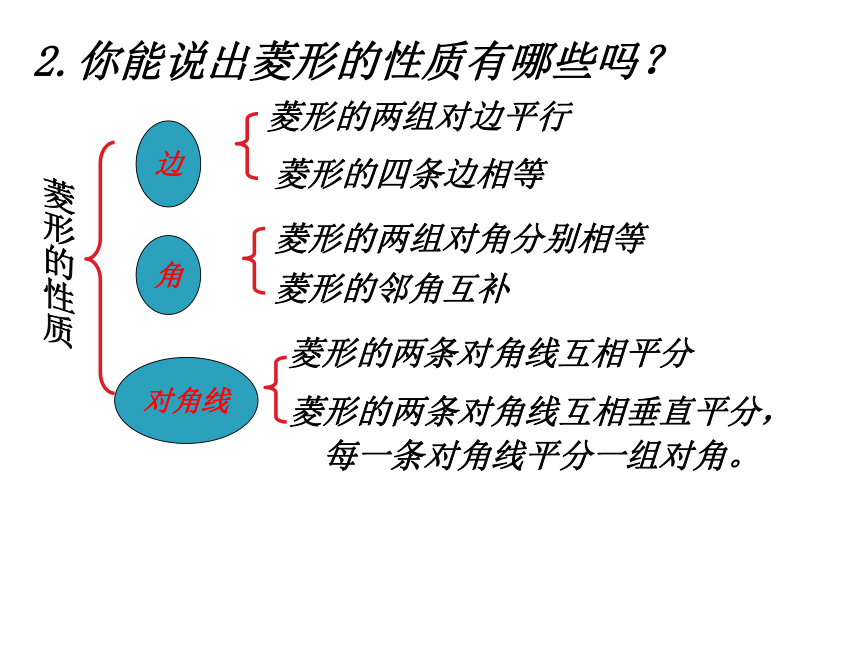
边
对角线
角
菱形的性质
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。
2.你能说出菱形的性质有哪些吗?
根据菱形的定义,可得菱形的判定方法1:
有一组邻边相等的平行四边形叫做菱形.
数学语言:
∵四边形ABCD是平行四边形,
且AB=AD,
∴四边形ABCD是菱形.
菱形还有其他的判定方法吗?
A
B
C
D
O
活动三:合作交流,探索新知
类比学习平行四边形和矩形的判定过程,研究菱形性质定理的逆命题, 你能找到菱形判定的其他方法吗?
猜想1:对角线互相垂直的平行四边形是菱形.
猜想2:四条边都相等的四边形是菱形.
猜想1:对角线互相垂直的平行四边形是菱形.
已知:四边形ABCD 是平行四边形,且
求证:平行四边形ABCD 是菱形.
对角线互相垂直的平行四边形是菱形.
结论:菱形判定方法2
.
猜想2:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
结论:菱形判定方法3
四条边都相等的四边形是菱形.
D
C
A
B
例1.如图,□ABCD的对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证: □ABCD是菱形.
证明:z````x``xk
∵AB=5,AO=4,BO=3,
∴
∴△OAB是直角三角形, AC⊥ BD.
∴ □ABCD是菱形.
活动四:应用新知,解决问题
例2. 已知:如图 ,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
你有几种方法?
O
F
E
A
D
C
B
例3 如图,AD平分∠BAC,DE∥AC交AB于点E,
DF∥AB交AC于点F.求证:四边形AEDF是菱形.
A
B
C
D
E
F
1.填空:
(1)对角线互相平分的四边形是 ;
(2)对角线互相垂直平分的四边形是________;
(3)对角线相等且互相平分的四边形是________;
(4)两组对边分别平行,且对角线 的四边形是菱形.
2.如图,O是矩形ABCD的对角线的交点,
DE∥AC,CE∥BD,DE和CE相交于E.
求证:四边形OCED是菱形.
平行四边形
菱形
矩形
互相垂直
活动五:课堂练习,巩固提高
3、如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
A
B
F
N
D
M
E
C
4、如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,四边形AEFG是菱形吗?
1.本节课你学到了哪些知识?在学习知识的过程中,你体会或者应用到了哪些思想方法?
2. 你能归纳出菱形所有的判定方法吗?
3.本节课你还存在什么疑惑吗?
判定方法1:有一组邻边相等的平行四边形是菱形.
判定方法2:对角线互相垂直的平行四边形是菱形.
判定方法3:四条边都相等的四边形是菱形.
活动六:本课小结
18.2.2 菱形
第2课时
18.2 特殊的平行四边形
课前预习:课本57---58
预习目标:
1、回顾矩形的定义、性质及判定。菱形的定义和性质。
2、探讨菱形有哪些判定方法?并会证明。
3、会灵活运用菱形的判定方法解决问题。
4、说一说本节课的收获。
活动一:回顾反思 类比猜想
我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?
矩形的
定义
有一个角是直角的平行四边形叫做矩形
矩形的
性质
具有平行四边形的所有性质
对角线相等
四个角都是直角
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
C
D
A
B
O
矩形的
判定
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
?
你的想法正确吗?
如何证明你的猜想?
1.菱形的定义是什么?
有一组邻边相等的平行四边形叫做菱形.
一组邻边相等
平行四边形
菱形
活动二:创设情景,引入新课
边
对角线
角
菱形的性质
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。
2.你能说出菱形的性质有哪些吗?
根据菱形的定义,可得菱形的判定方法1:
有一组邻边相等的平行四边形叫做菱形.
数学语言:
∵四边形ABCD是平行四边形,
且AB=AD,
∴四边形ABCD是菱形.
菱形还有其他的判定方法吗?
A
B
C
D
O
活动三:合作交流,探索新知
类比学习平行四边形和矩形的判定过程,研究菱形性质定理的逆命题, 你能找到菱形判定的其他方法吗?
猜想1:对角线互相垂直的平行四边形是菱形.
猜想2:四条边都相等的四边形是菱形.
猜想1:对角线互相垂直的平行四边形是菱形.
已知:四边形ABCD 是平行四边形,且
求证:平行四边形ABCD 是菱形.
对角线互相垂直的平行四边形是菱形.
结论:菱形判定方法2
.
猜想2:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
结论:菱形判定方法3
四条边都相等的四边形是菱形.
D
C
A
B
例1.如图,□ABCD的对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证: □ABCD是菱形.
证明:z````x``xk
∵AB=5,AO=4,BO=3,
∴
∴△OAB是直角三角形, AC⊥ BD.
∴ □ABCD是菱形.
活动四:应用新知,解决问题
例2. 已知:如图 ,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
你有几种方法?
O
F
E
A
D
C
B
例3 如图,AD平分∠BAC,DE∥AC交AB于点E,
DF∥AB交AC于点F.求证:四边形AEDF是菱形.
A
B
C
D
E
F
1.填空:
(1)对角线互相平分的四边形是 ;
(2)对角线互相垂直平分的四边形是________;
(3)对角线相等且互相平分的四边形是________;
(4)两组对边分别平行,且对角线 的四边形是菱形.
2.如图,O是矩形ABCD的对角线的交点,
DE∥AC,CE∥BD,DE和CE相交于E.
求证:四边形OCED是菱形.
平行四边形
菱形
矩形
互相垂直
活动五:课堂练习,巩固提高
3、如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
A
B
F
N
D
M
E
C
4、如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,四边形AEFG是菱形吗?
1.本节课你学到了哪些知识?在学习知识的过程中,你体会或者应用到了哪些思想方法?
2. 你能归纳出菱形所有的判定方法吗?
3.本节课你还存在什么疑惑吗?
判定方法1:有一组邻边相等的平行四边形是菱形.
判定方法2:对角线互相垂直的平行四边形是菱形.
判定方法3:四条边都相等的四边形是菱形.
活动六:本课小结
