人教版八年级数学下册课件:19.1.1函数(共21张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.1.1函数(共21张PPT) | 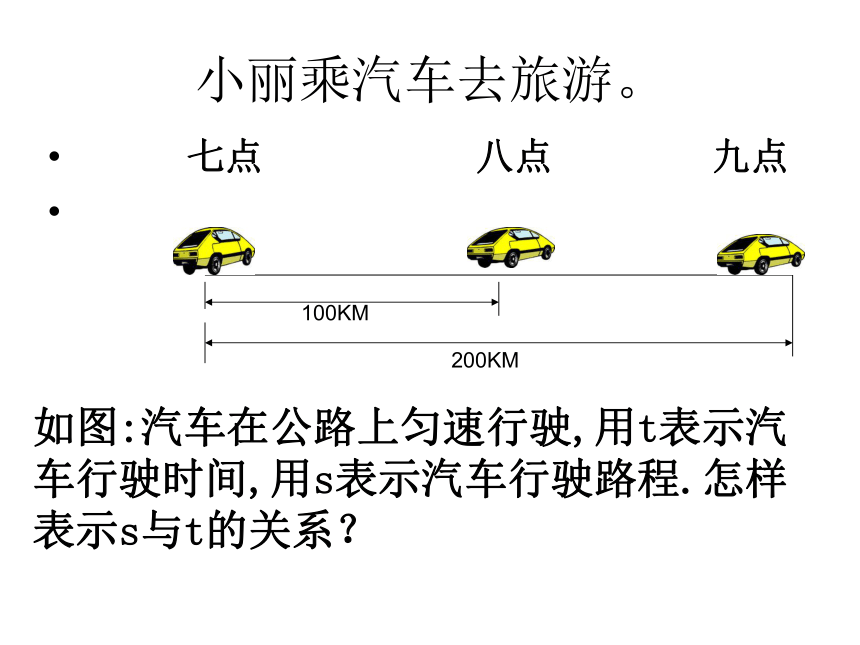 | |
| 格式 | ppt | ||
| 文件大小 | 875.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 23:46:28 | ||
图片预览






文档简介
小丽乘汽车去旅游。
七点 八点 九点
100KM
200KM
如图:汽车在公路上匀速行驶,用t表示汽车行驶时间,用s表示汽车行驶路程.怎样表示s与t的关系?
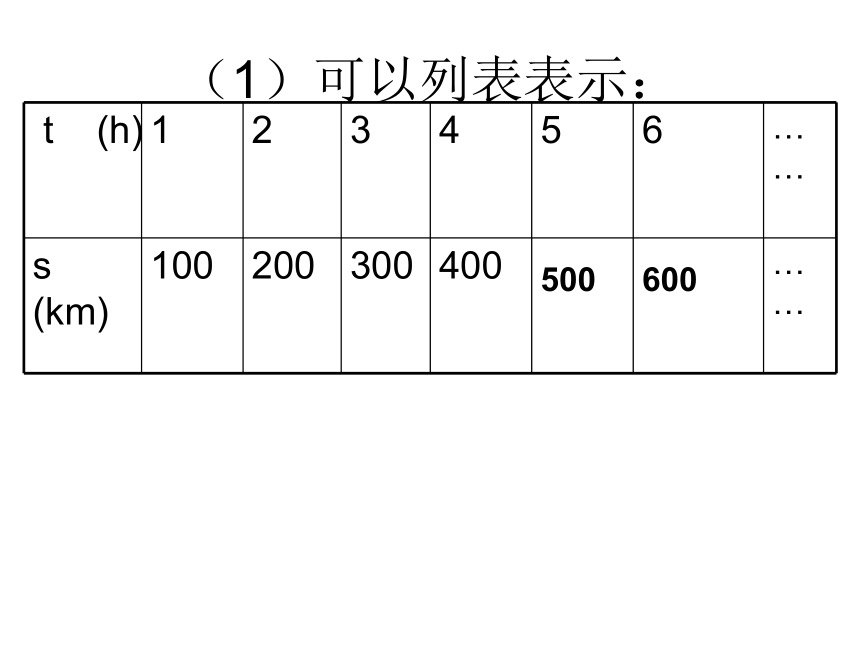
(1)可以列表表示:
t (h)
1
2
3
4
5
6
……
s (km)
100
200
300
400
……
500
600
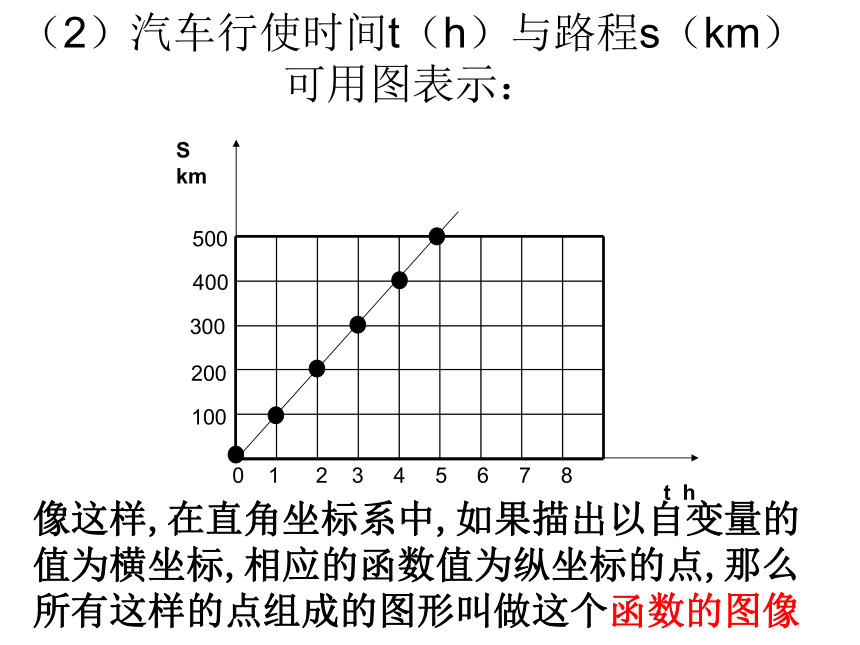
(2)汽车行使时间t(h)与路程s(km)可用图表示:
t h
0 1 2 3 4 5 6 7 8
500
400
300
200
100
S km
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应的函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图像
(3)怎样用式子表示汽车行驶路程与时间的关系呢?
s=100t
表示两个变量之间关系的式子通常称为函数关系式
例如:s=100t 就称为 s 与 t 的函数关系式
问题:变量s是变量t的函数吗?为什么?
是
函数
----函数的表示方法
通常,表示2个变量之间的关系可用3种方法:
——————、 —————、—————————— 。
函数关系式
列表
图像
例题分析:
例1、求下列函数的自变量取值范围:
y=13x-4;
y=
b=
x=
例2:汽车油箱内存油40L,每行驶100km耗油10L,求行驶过程中油箱内剩余油量Q (L)与行驶路程S ( km)的函数关系式.
(1)求当行驶了250km时,油箱中的余油量是多少?
(2)求当油箱中的余油量是5 L时,汽车行驶了多少k m 路程?
(3)当行驶路程s=___时,油箱内的存油用完.
(4)你能说出自变量s的取值范围吗?
在一个变化过程中,自变量的取值通常有一定的范围.例如,例1中自变量是在0≤S≤400, 我们把自变量取值的这个范围叫做自变量的取值范围。
在例题中,给定一个自变量的值,就可以求出对应的函数值。
实际问题中,确定自变量的取值范围时,除使所列代数式有意义外,还必须使实际问题有意义.
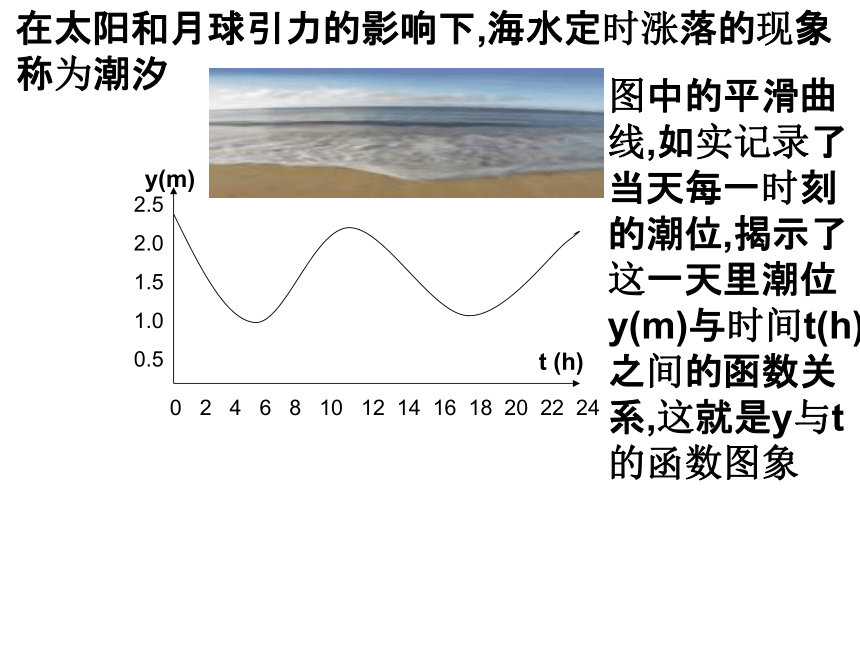
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐
0 2 4 6 8 10 12 14 16 18 20 22 24
2.5
2.0
1.5
1.0
0.5
图中的平滑曲线,如实记录了当天每一时刻的潮位,揭示了这一天里潮位y(m)与时间t(h)之间的函数关系,这就是y与t的函数图象
y(m)
t (h)
例3 小明骑自行车从甲地到乙地,图中的折线表示小明的行程S(千米)和所花时间t(小时)之间的函数关系.
例题讲解
(1)他在路上花了多长时间?
(2)折线中有一条平行与t轴的线段,试说明它的意义.
(3)出发后5小时,他离甲地有多远 ?
(4)自变量t的取值范围是多少?
随堂练习
1. 一根蜡烛长20cm,每小时燃掉5cm.
(1)写出蜡烛剩余的长度y(cm)与燃烧时间x(h)
之间的函数解析式.
(2)写出自变量x可以取值的范围;
(3)蜡烛点燃2h后还剩多长?
2.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是分别是_____.(只需填序号).
3、如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,读图填空:
①??? 这是一次 赛跑.
②??? 先到终点的是________.
③??? 王平在赛跑中速度是 m/s
0 92 100 t(s)
500
S (m)
李明 王平
五、拓展提高:
1.等腰三角形周长为12,求底边y与腰长x之间的函数关系式,并求出自变量x的取值范围是什么?
看函数图像
2.如图,边长为1和2的两个正方形的一边在同一水平线上,小正方形沿水平线自左向右匀速穿过大正方形,下图反映了这个运动的全过程.设小正方形的运动时间为t,两正方形重叠部分面积为S,则S与t的函数图象大致为( ).
3.如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
⑴甲出发几小时,乙才开始出发
⑵乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
⑶甲从下午2时到5时的速度是多少?
⑷乙行驶的速度是多少?
4.已知动点P以每秒2厘米的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△PAB的面积S关于时间t的函数图象如图乙.
(1)a的值是多少;
(2)求图甲中图形的面积;(3)求图乙中b的值.
5.梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过l0千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( ).
(A)1个 (B)2个
(C)3个 (D) 4个
6.某市的出租车的收费标准如下:3千米以内的收费6元;3千米到10千米部分每千米加收1.3元;10千米以上的部分每千米加收1.9元.那么出租车收费y(元)与行驶的路程x(千米)之间的函数关系式是什么?
课堂小结:
(1)表示两个变量间的关系的方法。
(2)从图象中获得信息并能用语言合理的表示,并能结合具体的情境理解图象上的点所表示的数学意义。
( 3)能根据实际问题的意义以及函数关系式,确定函数的自变量取值范围,并会求出函数值。
七点 八点 九点
100KM
200KM
如图:汽车在公路上匀速行驶,用t表示汽车行驶时间,用s表示汽车行驶路程.怎样表示s与t的关系?
(1)可以列表表示:
t (h)
1
2
3
4
5
6
……
s (km)
100
200
300
400
……
500
600
(2)汽车行使时间t(h)与路程s(km)可用图表示:
t h
0 1 2 3 4 5 6 7 8
500
400
300
200
100
S km
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应的函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图像
(3)怎样用式子表示汽车行驶路程与时间的关系呢?
s=100t
表示两个变量之间关系的式子通常称为函数关系式
例如:s=100t 就称为 s 与 t 的函数关系式
问题:变量s是变量t的函数吗?为什么?
是
函数
----函数的表示方法
通常,表示2个变量之间的关系可用3种方法:
——————、 —————、—————————— 。
函数关系式
列表
图像
例题分析:
例1、求下列函数的自变量取值范围:
y=13x-4;
y=
b=
x=
例2:汽车油箱内存油40L,每行驶100km耗油10L,求行驶过程中油箱内剩余油量Q (L)与行驶路程S ( km)的函数关系式.
(1)求当行驶了250km时,油箱中的余油量是多少?
(2)求当油箱中的余油量是5 L时,汽车行驶了多少k m 路程?
(3)当行驶路程s=___时,油箱内的存油用完.
(4)你能说出自变量s的取值范围吗?
在一个变化过程中,自变量的取值通常有一定的范围.例如,例1中自变量是在0≤S≤400, 我们把自变量取值的这个范围叫做自变量的取值范围。
在例题中,给定一个自变量的值,就可以求出对应的函数值。
实际问题中,确定自变量的取值范围时,除使所列代数式有意义外,还必须使实际问题有意义.
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐
0 2 4 6 8 10 12 14 16 18 20 22 24
2.5
2.0
1.5
1.0
0.5
图中的平滑曲线,如实记录了当天每一时刻的潮位,揭示了这一天里潮位y(m)与时间t(h)之间的函数关系,这就是y与t的函数图象
y(m)
t (h)
例3 小明骑自行车从甲地到乙地,图中的折线表示小明的行程S(千米)和所花时间t(小时)之间的函数关系.
例题讲解
(1)他在路上花了多长时间?
(2)折线中有一条平行与t轴的线段,试说明它的意义.
(3)出发后5小时,他离甲地有多远 ?
(4)自变量t的取值范围是多少?
随堂练习
1. 一根蜡烛长20cm,每小时燃掉5cm.
(1)写出蜡烛剩余的长度y(cm)与燃烧时间x(h)
之间的函数解析式.
(2)写出自变量x可以取值的范围;
(3)蜡烛点燃2h后还剩多长?
2.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是分别是_____.(只需填序号).
3、如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,读图填空:
①??? 这是一次 赛跑.
②??? 先到终点的是________.
③??? 王平在赛跑中速度是 m/s
0 92 100 t(s)
500
S (m)
李明 王平
五、拓展提高:
1.等腰三角形周长为12,求底边y与腰长x之间的函数关系式,并求出自变量x的取值范围是什么?
看函数图像
2.如图,边长为1和2的两个正方形的一边在同一水平线上,小正方形沿水平线自左向右匀速穿过大正方形,下图反映了这个运动的全过程.设小正方形的运动时间为t,两正方形重叠部分面积为S,则S与t的函数图象大致为( ).
3.如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
⑴甲出发几小时,乙才开始出发
⑵乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
⑶甲从下午2时到5时的速度是多少?
⑷乙行驶的速度是多少?
4.已知动点P以每秒2厘米的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△PAB的面积S关于时间t的函数图象如图乙.
(1)a的值是多少;
(2)求图甲中图形的面积;(3)求图乙中b的值.
5.梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过l0千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( ).
(A)1个 (B)2个
(C)3个 (D) 4个
6.某市的出租车的收费标准如下:3千米以内的收费6元;3千米到10千米部分每千米加收1.3元;10千米以上的部分每千米加收1.9元.那么出租车收费y(元)与行驶的路程x(千米)之间的函数关系式是什么?
课堂小结:
(1)表示两个变量间的关系的方法。
(2)从图象中获得信息并能用语言合理的表示,并能结合具体的情境理解图象上的点所表示的数学意义。
( 3)能根据实际问题的意义以及函数关系式,确定函数的自变量取值范围,并会求出函数值。
