人教版八年级数学下册课件:19.2.1正比例函数图像(共51张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.2.1正比例函数图像(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览







文档简介
一次函数的图像
神秘的
探究
路径
什么是函数图像?
01
如何做正比例函数的图像?
02
正比例函数图像的性质
03
总结和练习
04
什么是函数图象?
01
A
B
C
D
什么是函数图像?
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象 。
01
02
04
03
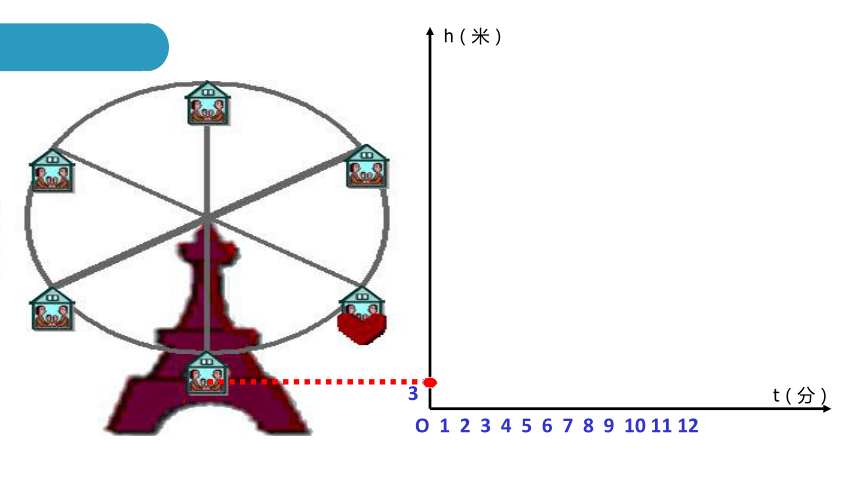
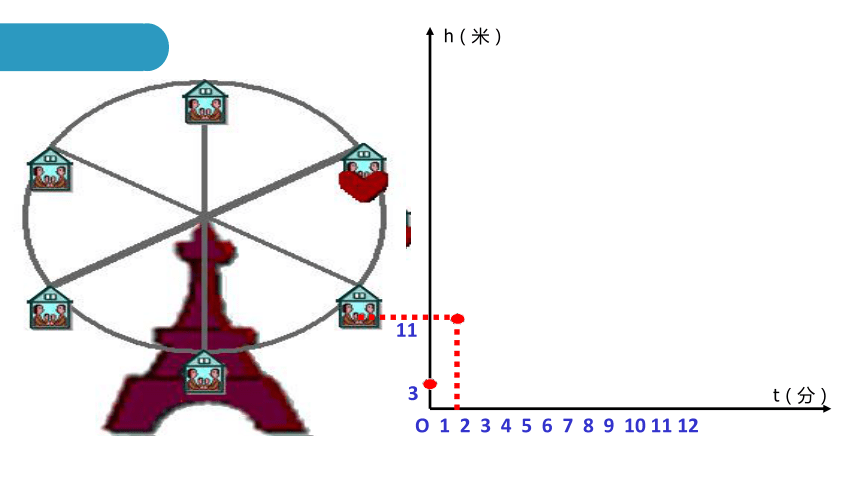
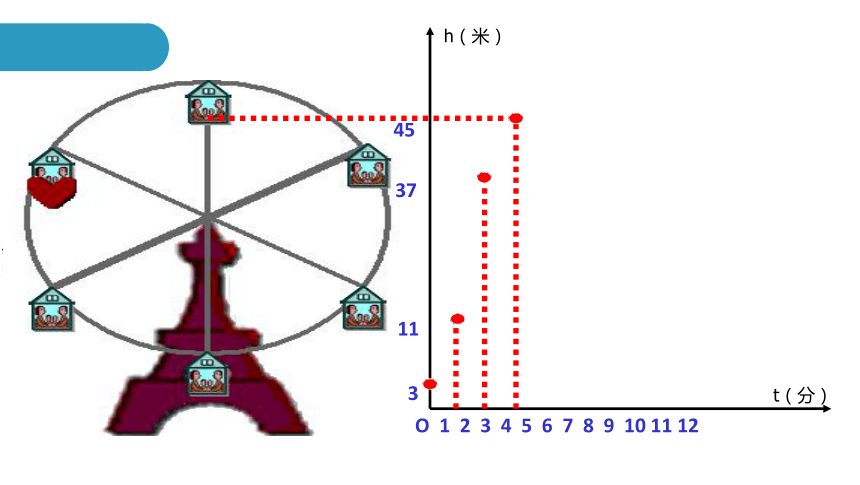
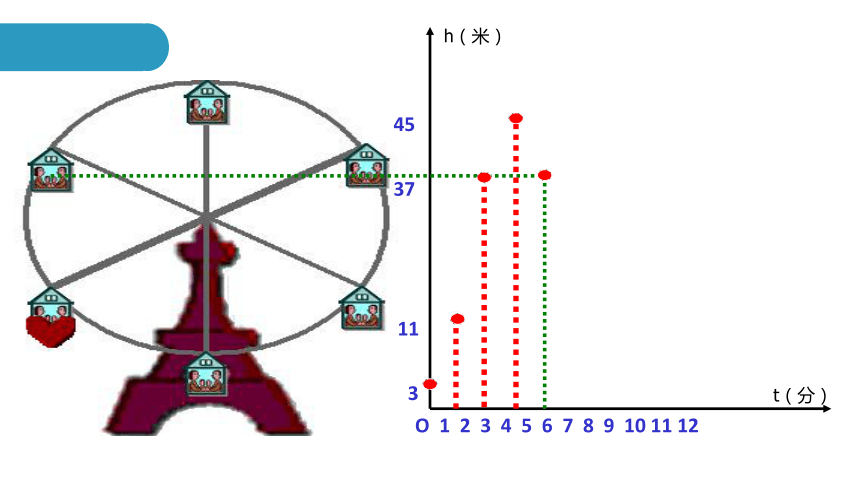
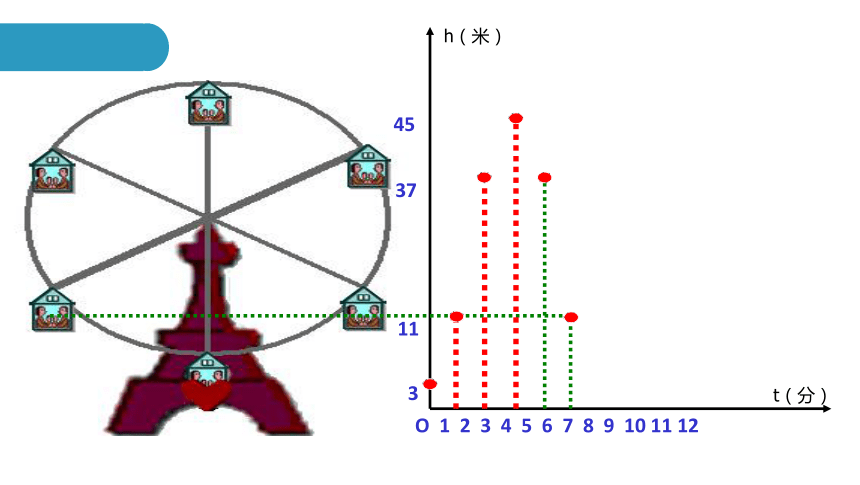
摩天轮的高度变化的函数图像
你还记得吗?
4分钟
3分钟
2分钟
1分钟
摩天轮的高度随着时间的变化而变化
一个时间对应一个高度
O 1 2 3 4 5 6 7 8 9 10 11 12
3
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
t/分
0
1
2
3
4
5
……
h/米
……
11
37
45
37
3
下图反映了旋转时间t(分)与摩天轮上的一点的高度h (米)之间的关系。
10
如何做正比例函数图像?
02
正比例函数是特殊的一次函数。
正比例函数的关系式
y=kx(k为常数,k≠0)
探究一次函数图像?
先研究简单的正比例函数图像
列表
找点
连线
如何做出摩天轮的图像?
知道正比例函数关系式,如何画出图像?
做正比例函数的图象
例1 请画出正比例函数y=2x的图象.
解:列表:
x
…
-2
-1
0
1
2
…
y=2x
…
…
转化为坐标
列表
描点
几何画板演示
描点
正比例函数y=2x的图象
描点
连线
正比例函数的图象
y=2x
连线
连线
03
动画演示
04
描点
02
列表
01
Option 01
Option 02
Option 03
Option 04
活动一:
两人为一组,在同一直角坐标系中通过(列表,描点,连线),
一人画y=x,y=3x;,另一人画y=-2x,y=-3x,比一比哪组画的又快又好?
正比例函数图像是一条直线。
直线公理:两点确定一条直线
正比例函数y=kx的图像是经过原点(0,0)的直线,
所以只需要再找一个点(1,k)就可以了。
获胜秘籍
1
2
3
正比例函数y=kx的图像是经过原点(0,0)的直线,所以只需要再找一个点(1,k)就可以了。
结
论
一
动手操作,深化探索 (做一做 )
观察对比正比例函数y=x,y=3x,y=-2x,y=-3x 图像是什么?是否经过原点?分别经过哪些象限?
探究正比例函数图像的性质
03
y=x
y=kx
y=-4x
y=3x
活动二
请根据关系式,描述出对应的函数图像
动手操作,深化探索 (试一试 )
k是解开正比例函数图像钥匙。
思考1:正比例函数图像的是什么?
思考2.正比例函数图像的位置为什么会不同?
思考3.k值如何影响函数图象的位置?
0.5 秒延迟符,无
意义,可删除.
探究一:
y=-2x
y=x
y=-3x
y=2x
结论二
1.
当k>0时,直线经过第 象限.
2.
当k>0时,直线经过第 象限.
正比例函数y=kx(k≠0)的图像中
动手操作,深化探索 (做一做 )
(1)观察正比例函数y=x,y=3x,y=-2x,y=-3x图像。
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否都满足关系式.
正比例函数图像上点的横、纵坐标所代表的x,y值都满足
该函数的关系式;
满足函数关系式的x,y所对应的点都在正比例函数的图像上。
01
02
04
03
x的值变化,y的值分别如何变化?
探究二:
几何画板演示
正比例函数中k值对函数增减性的影响。
动画演示
正比例函数中k值对函数增减性的影响。
当k>0时,图像在 象限,y 的值随x的值增大而 ;
当k>0时,图像在 象限,y 的值随x的值增大而 。
结论三
k>o
k根据图像,
思考y=x,y=3x,
哪一个函数y的值
随x的增大,
增长的更快?
根据图像,
思考y=-2x,y=-3x,
哪一个函数y的值
随x的增大,
减小的更快?
正比例函数y=kx(k≠0)中,k的绝对值越大直线越陡。
结
论
四
1.图像的位置
2.函数的增减性
正比例函数y=kx中的k对图像有哪些影响?
3.直线的倾斜度
课堂练习
04
1.写出图中直线所对应的函数表达式。
2.下列哪些点在正比例函数y=-5x的图像上?
(1,5) ,(-1,5), (0.5,2.5) , ( -5,1)
3.下列正比例函数中,y的值随着x值的增大而减小的有
4. 已知正比例函数y=(3-k)x,
(1)若y的值随x的增大而增大,则k的取值范围是什么?
(2)若y的值随x的增大而减小,则k的取值范围是什么?
快速回答
正比例函数图像如图:
(1)a,b的正负?
(2)函数的增减性?
(3)a,b的绝对值的大小?
y=ax
y=bx
正比例函数图像如图:
(1)c,d的正负?
(2)函数的增减性?
(3)c,d的大小?
快速回答
我们的收获
05
探究
收获
什么是函数图像?
01
如何做正比例函数的图像?
02
正比例函数中k的重要性
03
1.图像的位置
2.函数的增减性
正比例函数y=kx中的k对图像有哪些影响?
3.直线的倾斜度
探究待续
作图
分析
总结
神秘的
探究
路径
什么是函数图像?
01
如何做正比例函数的图像?
02
正比例函数图像的性质
03
总结和练习
04
什么是函数图象?
01
A
B
C
D
什么是函数图像?
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象 。
01
02
04
03
摩天轮的高度变化的函数图像
你还记得吗?
4分钟
3分钟
2分钟
1分钟
摩天轮的高度随着时间的变化而变化
一个时间对应一个高度
O 1 2 3 4 5 6 7 8 9 10 11 12
3
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
O 1 2 3 4 5 6 7 8 9 10 11 12
3
11
37
45
h(米)
t(分)
t/分
0
1
2
3
4
5
……
h/米
……
11
37
45
37
3
下图反映了旋转时间t(分)与摩天轮上的一点的高度h (米)之间的关系。
10
如何做正比例函数图像?
02
正比例函数是特殊的一次函数。
正比例函数的关系式
y=kx(k为常数,k≠0)
探究一次函数图像?
先研究简单的正比例函数图像
列表
找点
连线
如何做出摩天轮的图像?
知道正比例函数关系式,如何画出图像?
做正比例函数的图象
例1 请画出正比例函数y=2x的图象.
解:列表:
x
…
-2
-1
0
1
2
…
y=2x
…
…
转化为坐标
列表
描点
几何画板演示
描点
正比例函数y=2x的图象
描点
连线
正比例函数的图象
y=2x
连线
连线
03
动画演示
04
描点
02
列表
01
Option 01
Option 02
Option 03
Option 04
活动一:
两人为一组,在同一直角坐标系中通过(列表,描点,连线),
一人画y=x,y=3x;,另一人画y=-2x,y=-3x,比一比哪组画的又快又好?
正比例函数图像是一条直线。
直线公理:两点确定一条直线
正比例函数y=kx的图像是经过原点(0,0)的直线,
所以只需要再找一个点(1,k)就可以了。
获胜秘籍
1
2
3
正比例函数y=kx的图像是经过原点(0,0)的直线,所以只需要再找一个点(1,k)就可以了。
结
论
一
动手操作,深化探索 (做一做 )
观察对比正比例函数y=x,y=3x,y=-2x,y=-3x 图像是什么?是否经过原点?分别经过哪些象限?
探究正比例函数图像的性质
03
y=x
y=kx
y=-4x
y=3x
活动二
请根据关系式,描述出对应的函数图像
动手操作,深化探索 (试一试 )
k是解开正比例函数图像钥匙。
思考1:正比例函数图像的是什么?
思考2.正比例函数图像的位置为什么会不同?
思考3.k值如何影响函数图象的位置?
0.5 秒延迟符,无
意义,可删除.
探究一:
y=-2x
y=x
y=-3x
y=2x
结论二
1.
当k>0时,直线经过第 象限.
2.
当k>0时,直线经过第 象限.
正比例函数y=kx(k≠0)的图像中
动手操作,深化探索 (做一做 )
(1)观察正比例函数y=x,y=3x,y=-2x,y=-3x图像。
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否都满足关系式.
正比例函数图像上点的横、纵坐标所代表的x,y值都满足
该函数的关系式;
满足函数关系式的x,y所对应的点都在正比例函数的图像上。
01
02
04
03
x的值变化,y的值分别如何变化?
探究二:
几何画板演示
正比例函数中k值对函数增减性的影响。
动画演示
正比例函数中k值对函数增减性的影响。
当k>0时,图像在 象限,y 的值随x的值增大而 ;
当k>0时,图像在 象限,y 的值随x的值增大而 。
结论三
k>o
k
思考y=x,y=3x,
哪一个函数y的值
随x的增大,
增长的更快?
根据图像,
思考y=-2x,y=-3x,
哪一个函数y的值
随x的增大,
减小的更快?
正比例函数y=kx(k≠0)中,k的绝对值越大直线越陡。
结
论
四
1.图像的位置
2.函数的增减性
正比例函数y=kx中的k对图像有哪些影响?
3.直线的倾斜度
课堂练习
04
1.写出图中直线所对应的函数表达式。
2.下列哪些点在正比例函数y=-5x的图像上?
(1,5) ,(-1,5), (0.5,2.5) , ( -5,1)
3.下列正比例函数中,y的值随着x值的增大而减小的有
4. 已知正比例函数y=(3-k)x,
(1)若y的值随x的增大而增大,则k的取值范围是什么?
(2)若y的值随x的增大而减小,则k的取值范围是什么?
快速回答
正比例函数图像如图:
(1)a,b的正负?
(2)函数的增减性?
(3)a,b的绝对值的大小?
y=ax
y=bx
正比例函数图像如图:
(1)c,d的正负?
(2)函数的增减性?
(3)c,d的大小?
快速回答
我们的收获
05
探究
收获
什么是函数图像?
01
如何做正比例函数的图像?
02
正比例函数中k的重要性
03
1.图像的位置
2.函数的增减性
正比例函数y=kx中的k对图像有哪些影响?
3.直线的倾斜度
探究待续
作图
分析
总结
