人教版八年级下册 18.2.2菱形的性质(第1课时) 课件(共21张PPT)
文档属性
| 名称 | 人教版八年级下册 18.2.2菱形的性质(第1课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 640.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览


文档简介
人教版八年级数学
第十八章 平行四边形
18.2.2菱形的性质(第一课时)
课标解读
1.理解菱形的定义,能够分辨平行四边形与菱形的区别和联系。
2.掌握菱形的性质定理,并能运用菱形的性质定理进行简单的计算与证明
知识梳理
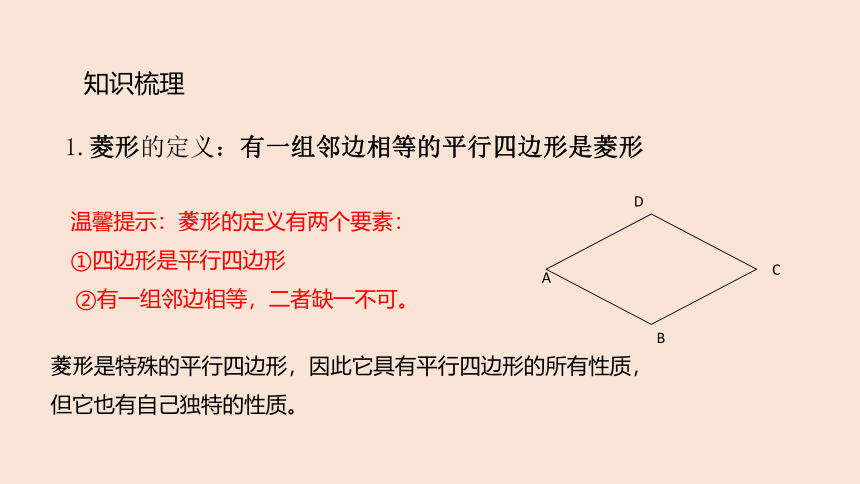
1.菱形的定义:有一组邻边相等的平行四边形是菱形
温馨提示:菱形的定义有两个要素:
①四边形是平行四边形
②有一组邻边相等,二者缺一不可。
菱形是特殊的平行四边形,因此它具有平行四边形的所有性质,但它也有自己独特的性质。
A
B
C
D
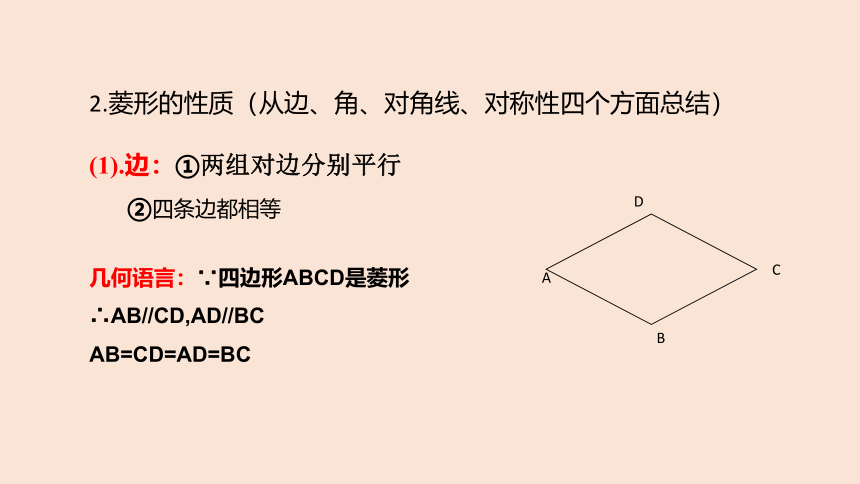
2.菱形的性质(从边、角、对角线、对称性四个方面总结)
(1).边:①两组对边分别平行
②四条边都相等
几何语言:∵四边形ABCD是菱形
∴AB//CD,AD//BC
AB=CD=AD=BC
A
B
C
D
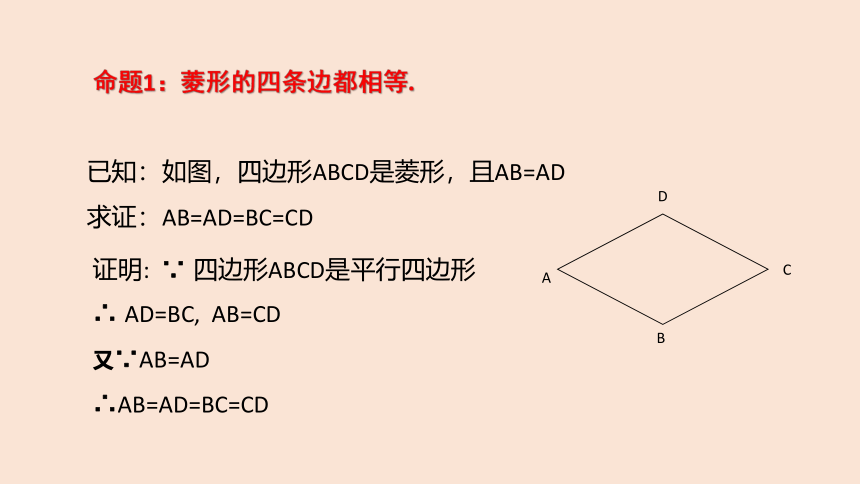
命题1:菱形的四条边都相等.
A
B
D
C
已知:如图,四边形ABCD是菱形,且AB=AD
求证:AB=AD=BC=CD
证明: ∵ 四边形ABCD是平行四边形
∴ AD=BC, AB=CD
又∵AB=AD
∴AB=AD=BC=CD
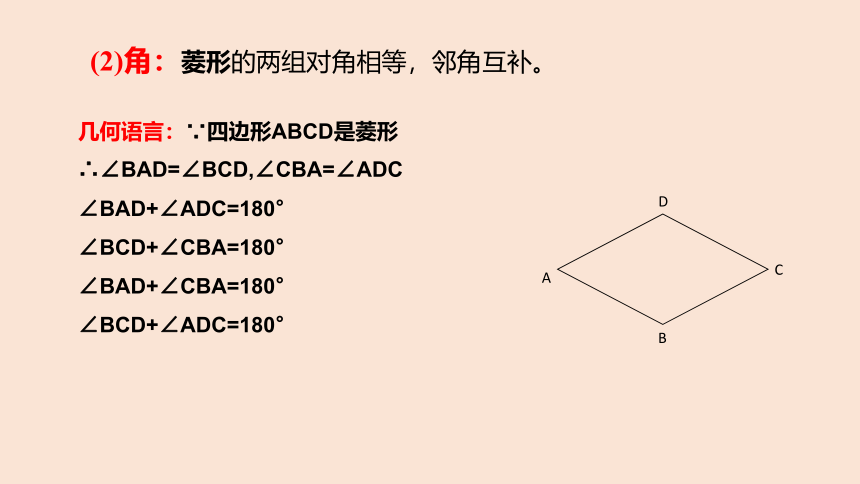
(2)角:菱形的两组对角相等,邻角互补。
几何语言:∵四边形ABCD是菱形
∴∠BAD=∠BCD,∠CBA=∠ADC
∠BAD+∠ADC=180°
∠BCD+∠CBA=180°
∠BAD+∠CBA=180°
∠BCD+∠ADC=180°
A
B
C
D
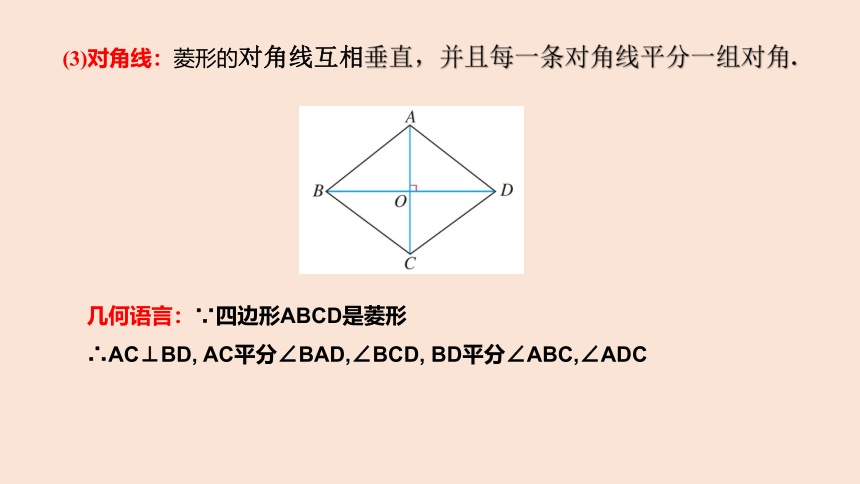
(3)对角线:菱形的对角线互相垂直,并且每一条对角线平分一组对角.
几何语言:∵四边形ABCD是菱形
∴AC⊥BD, AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
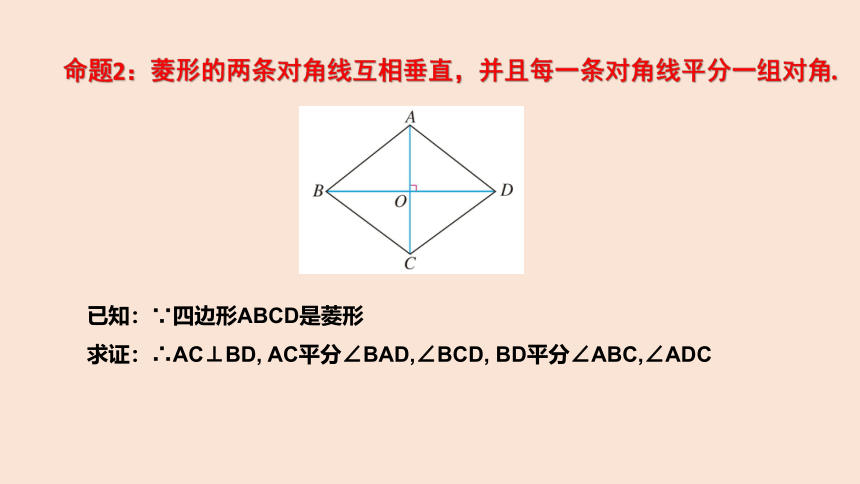
命题2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:∵四边形ABCD是菱形
求证:∴AC⊥BD, AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
已知:四边形ABCD是菱形
求证:AC⊥BD, AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
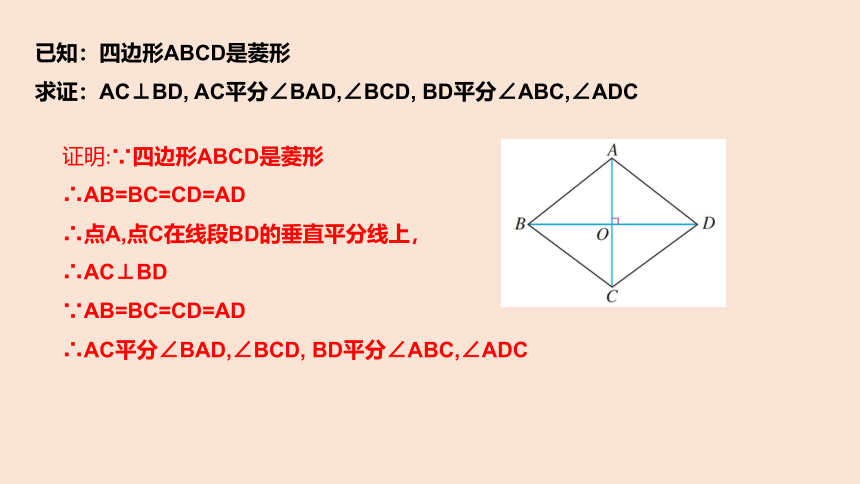
证明:∵四边形ABCD是菱形
∴AB=BC=CD=AD
∴点A,点C在线段BD的垂直平分线上,
∴AC⊥BD
∵AB=BC=CD=AD
∴AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
归纳总结:
菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.
(4)对称性:菱形既是轴对称图形,又是中心对称图形,有两条对称轴,其对称轴为两条对角线所在直线,对称中心为其对角线的交点。
3.菱形的面积:(1)面积=底×高
(2)面积=两条对角线的长的乘积的一半
S菱形ABCD= AC · BD
平行四边形的性质
矩形的性质
菱形的性质
对边平行且相等
对角相等,
邻角互补
对角线互相平分
4.平行四边形,矩形,菱形的区别和联系
对边平行且相等
四个角都是直角
四条边都相等
对角相等,
邻角互补
对角线互相平分
相等
对角线互相垂直
平分
例1: 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
解:∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO= ∠ABC= ×60°= 30°.
在Rt△OAB中,AO= AB= ×20=10(m),
BO= = = 10 (m)
∴花坛的两条小路长 AC=2AO=20(m),
BD=2BO= 20 ≈ 34.64(m).
花坛的面积 S菱形ABCD =4×S△ OAB
= AC·BD=200 ≈346.4(m2).
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4. 求AC和BD的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∴△ABO是直角三角形,
∴BO= =3
∴AC=2AO=8,BD=2BO=6
同步练习
2.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm,
求菱形的周长和面积.
解:菱形的边长= =5.
C菱形ABCD= 4×5=20(cm)
(cm)
3. 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( ) A. 1 B. C. 2 D. 2
C
4. 如图,?ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件________________________________________________,使其成为菱形( 只填一个即可).
AC⊥BD或AB=BC(?ABCD任意一组邻边相等均可)
5. 如图,在菱形ABCD中,对角线AC、BD相交于点O,OC=3,OD=4,则菱形ABCD的面积为________;周长为________.
24
20
1.菱形的两条对角线的长的比为3∶4,面积为24cm2,求菱形的周长.
解:设一条对角线长为3x,则另一条对角线长为4x,
S= ×3x·4x=24,∴x=2.
边长= =5.
∴菱形的周长=4×5=20(cm).
拓展提升
2.如图所示,把一张矩形纸片按如图所示对折两次,然后剪下一部分,若得到一个钝角为120°的菱形,则剪口与第二次折痕所成角的度数应为( )
A.30°或50° B.40°或50° C.30°或60° D.40°或60°
C
第十八章 平行四边形
18.2.2菱形的性质(第一课时)
课标解读
1.理解菱形的定义,能够分辨平行四边形与菱形的区别和联系。
2.掌握菱形的性质定理,并能运用菱形的性质定理进行简单的计算与证明
知识梳理
1.菱形的定义:有一组邻边相等的平行四边形是菱形
温馨提示:菱形的定义有两个要素:
①四边形是平行四边形
②有一组邻边相等,二者缺一不可。
菱形是特殊的平行四边形,因此它具有平行四边形的所有性质,但它也有自己独特的性质。
A
B
C
D
2.菱形的性质(从边、角、对角线、对称性四个方面总结)
(1).边:①两组对边分别平行
②四条边都相等
几何语言:∵四边形ABCD是菱形
∴AB//CD,AD//BC
AB=CD=AD=BC
A
B
C
D
命题1:菱形的四条边都相等.
A
B
D
C
已知:如图,四边形ABCD是菱形,且AB=AD
求证:AB=AD=BC=CD
证明: ∵ 四边形ABCD是平行四边形
∴ AD=BC, AB=CD
又∵AB=AD
∴AB=AD=BC=CD
(2)角:菱形的两组对角相等,邻角互补。
几何语言:∵四边形ABCD是菱形
∴∠BAD=∠BCD,∠CBA=∠ADC
∠BAD+∠ADC=180°
∠BCD+∠CBA=180°
∠BAD+∠CBA=180°
∠BCD+∠ADC=180°
A
B
C
D
(3)对角线:菱形的对角线互相垂直,并且每一条对角线平分一组对角.
几何语言:∵四边形ABCD是菱形
∴AC⊥BD, AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
命题2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:∵四边形ABCD是菱形
求证:∴AC⊥BD, AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
已知:四边形ABCD是菱形
求证:AC⊥BD, AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
证明:∵四边形ABCD是菱形
∴AB=BC=CD=AD
∴点A,点C在线段BD的垂直平分线上,
∴AC⊥BD
∵AB=BC=CD=AD
∴AC平分∠BAD,∠BCD, BD平分∠ABC,∠ADC
归纳总结:
菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.
(4)对称性:菱形既是轴对称图形,又是中心对称图形,有两条对称轴,其对称轴为两条对角线所在直线,对称中心为其对角线的交点。
3.菱形的面积:(1)面积=底×高
(2)面积=两条对角线的长的乘积的一半
S菱形ABCD= AC · BD
平行四边形的性质
矩形的性质
菱形的性质
对边平行且相等
对角相等,
邻角互补
对角线互相平分
4.平行四边形,矩形,菱形的区别和联系
对边平行且相等
四个角都是直角
四条边都相等
对角相等,
邻角互补
对角线互相平分
相等
对角线互相垂直
平分
例1: 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
解:∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO= ∠ABC= ×60°= 30°.
在Rt△OAB中,AO= AB= ×20=10(m),
BO= = = 10 (m)
∴花坛的两条小路长 AC=2AO=20(m),
BD=2BO= 20 ≈ 34.64(m).
花坛的面积 S菱形ABCD =4×S△ OAB
= AC·BD=200 ≈346.4(m2).
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4. 求AC和BD的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∴△ABO是直角三角形,
∴BO= =3
∴AC=2AO=8,BD=2BO=6
同步练习
2.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm,
求菱形的周长和面积.
解:菱形的边长= =5.
C菱形ABCD= 4×5=20(cm)
(cm)
3. 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( ) A. 1 B. C. 2 D. 2
C
4. 如图,?ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件________________________________________________,使其成为菱形( 只填一个即可).
AC⊥BD或AB=BC(?ABCD任意一组邻边相等均可)
5. 如图,在菱形ABCD中,对角线AC、BD相交于点O,OC=3,OD=4,则菱形ABCD的面积为________;周长为________.
24
20
1.菱形的两条对角线的长的比为3∶4,面积为24cm2,求菱形的周长.
解:设一条对角线长为3x,则另一条对角线长为4x,
S= ×3x·4x=24,∴x=2.
边长= =5.
∴菱形的周长=4×5=20(cm).
拓展提升
2.如图所示,把一张矩形纸片按如图所示对折两次,然后剪下一部分,若得到一个钝角为120°的菱形,则剪口与第二次折痕所成角的度数应为( )
A.30°或50° B.40°或50° C.30°或60° D.40°或60°
C
