人教版八年级下册17勾股定理(1)课件(共31张PPT)
文档属性
| 名称 | 人教版八年级下册17勾股定理(1)课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 23:52:35 | ||
图片预览







文档简介
(共31张PPT)
17勾股定理(1)
B
A
C
图甲 图乙
A的面积
B的面积
C的面积
4
4
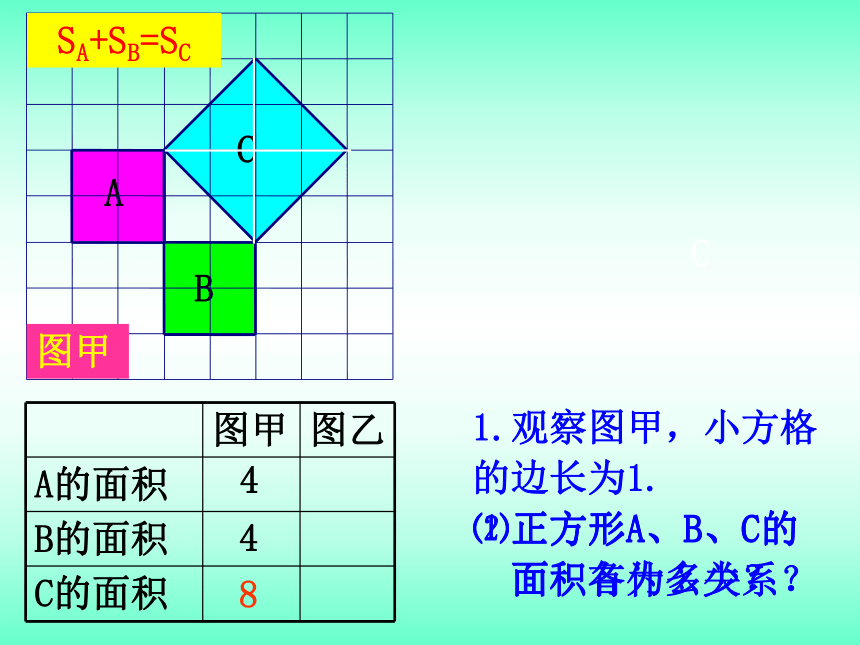
8
SA+SB=SC
C
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
A
B
C
图乙
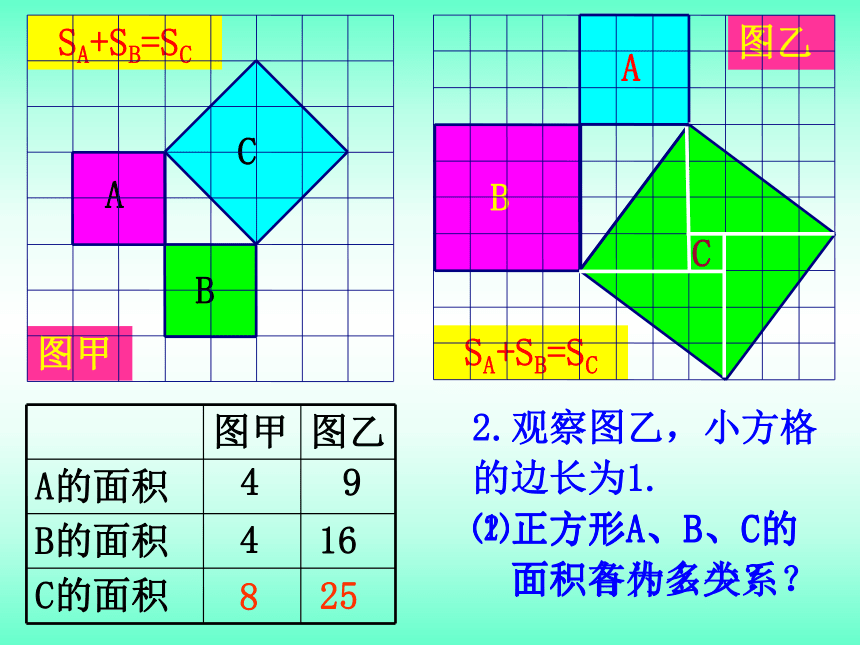
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
A
B
图乙
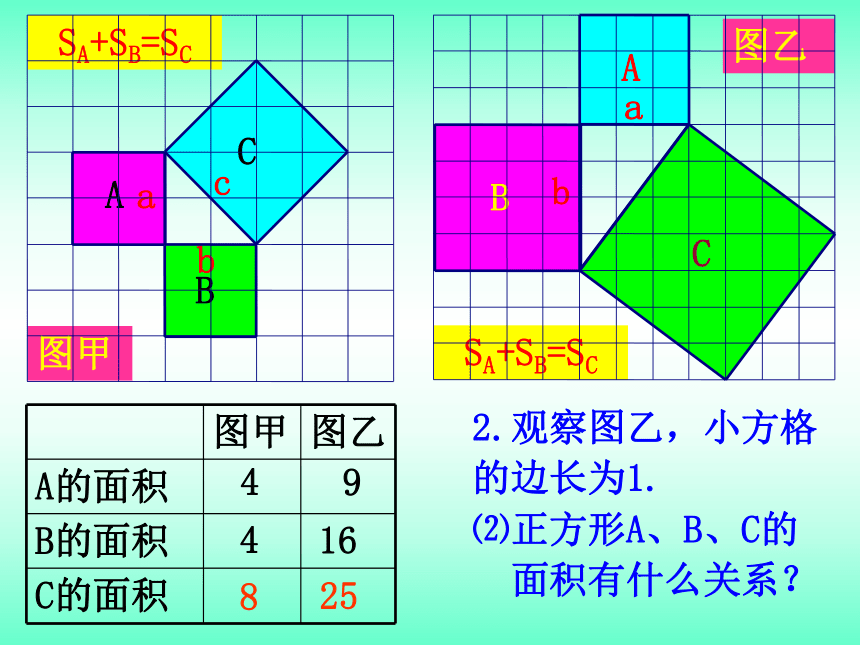
2.观察图乙,小方格
的边长为1.
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
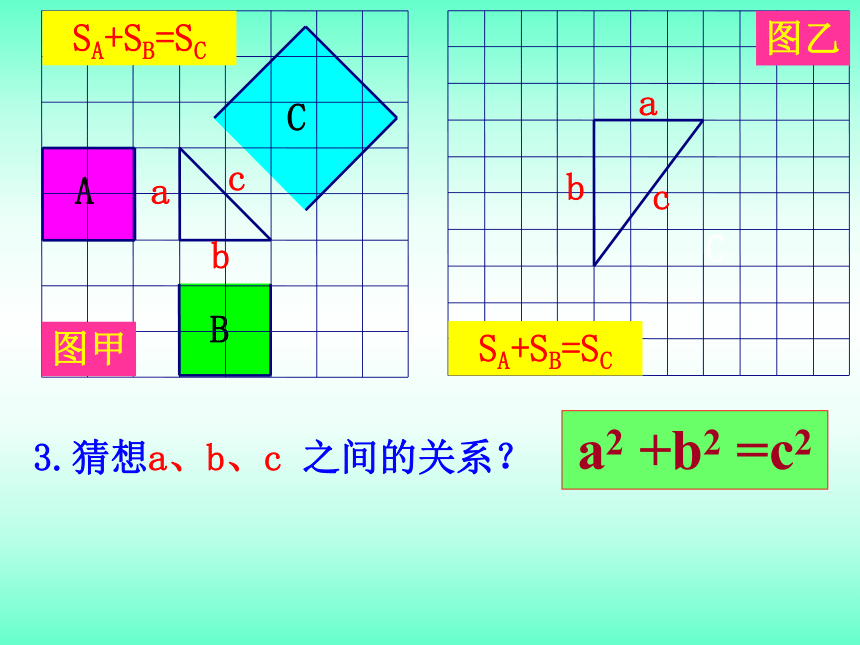
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
3.证明a、b、c 之间的关系?
a2 +b2 =c2
3.证明a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
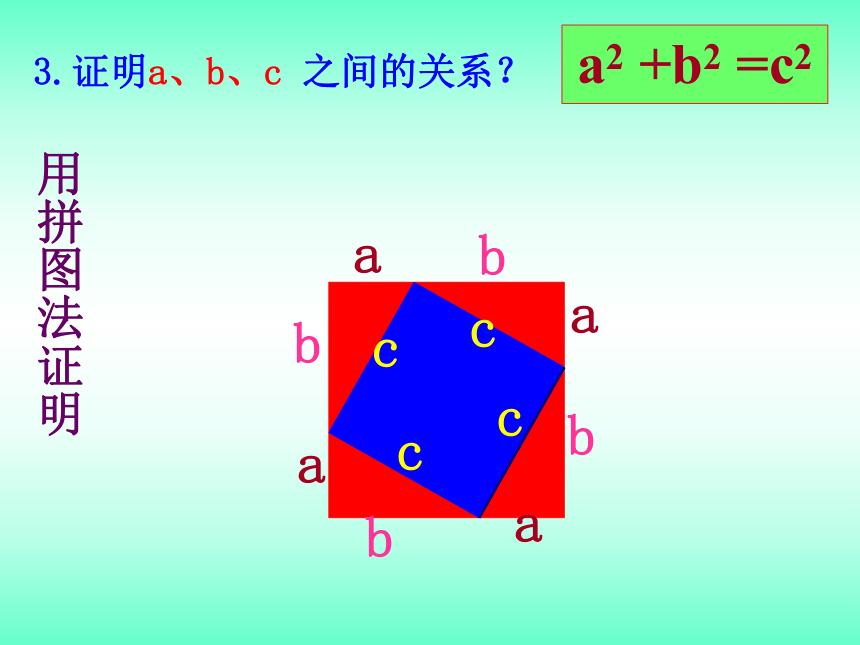
用拼图法证明
3.证明a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴ =
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
勾股定理(毕达哥拉斯定理)
(gou-gu theorem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于
斜边的平方.
a
c
勾
弦
b
股
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
a
b
c
a
b
c
例题
求x的值
16
20
x
A
C
B
(1分)
(1分)
(2分)
(1分)
(1分)
(2分)
(1分)
(3分)
(3分)
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
解:连结AC,在Rt△ABC中,
根据勾股定理得:
AC2=AB2+BC2=22+12=5
因此,AC=
因为AC______木板的宽,
所以木板____ 从门框内通过.
大于
能
≈2.236
A
B
C
D
1m
2m
1、本节课我们经历了怎样的学习过程?
经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。
3、学了本节课后你有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。
做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
如图,池塘边有两点A、B,无法直接测量AB之间的距离,请你运用所学过的知识设计一种方法,来测量AB间的距离。
比一比,哪位同学的方法既多又好?
要求:1、画出设计图
2、若涉及到角度,请直接标在设计图中
3、若涉及到长度,请用a、b、c等字母
B
A
1、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8m
B
C
A
6m
解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。
解:根据勾股定理得:
AB2= 92 + 122
=81+144
=225
即:AC=15
∴AC+AB=9+15=24(米)
答:旗杆折断前有10米。
2、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
9米
12米
A
B
C
C
A.8 米 B.9 米 C.10米 D.14米
1、如图,一个长8 米,宽6 米的草地,需在相对角的顶点间加一条小路,则小路的长为 ( )
8m
6m
别踩我,我怕疼!
求下图中表示边的未知数的值.
y
144
169
求下列直角三角形中未知边的长:
12
5
x
=625
225
400
A
225
81
B
=144
求下列图中字母所表示的正方形的面积
判断题:
ABC的两边AB=5,AC=12,则BC=13 ( )
5 或
4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
D
A
B
C
1、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
提示
构造直角三角形
在Rt△ABC中,∠C=90°
(1) 已知:a=6,b=8,求c;
(2) 已知:c=13,b=5,求a;
(3) 已知: a:b=3:4,c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
由勾股定理得: c2=a2+b2
=62+82
=100
∴c=10
方法
小结
由勾股定理得: a2=c2-b2
=132-52
=144
∴c=12
设a=3k b=4k
由勾股定理得: c2=a2+b2
=9k2+16k2
=25k2
∴c=5k
又∵c=15 ∴k=3
∴a=9 b=12
a
b
c
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
弦图
现在我们一起来探索“弦图”的奥妙吧!
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
公式变形
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
17勾股定理(1)
B
A
C
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
SA+SB=SC
C
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
A
B
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
A
B
图乙
2.观察图乙,小方格
的边长为1.
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
3.证明a、b、c 之间的关系?
a2 +b2 =c2
3.证明a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.证明a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴ =
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
勾股定理(毕达哥拉斯定理)
(gou-gu theorem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于
斜边的平方.
a
c
勾
弦
b
股
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
a
b
c
a
b
c
例题
求x的值
16
20
x
A
C
B
(1分)
(1分)
(2分)
(1分)
(1分)
(2分)
(1分)
(3分)
(3分)
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
解:连结AC,在Rt△ABC中,
根据勾股定理得:
AC2=AB2+BC2=22+12=5
因此,AC=
因为AC______木板的宽,
所以木板____ 从门框内通过.
大于
能
≈2.236
A
B
C
D
1m
2m
1、本节课我们经历了怎样的学习过程?
经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。
3、学了本节课后你有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。
做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
如图,池塘边有两点A、B,无法直接测量AB之间的距离,请你运用所学过的知识设计一种方法,来测量AB间的距离。
比一比,哪位同学的方法既多又好?
要求:1、画出设计图
2、若涉及到角度,请直接标在设计图中
3、若涉及到长度,请用a、b、c等字母
B
A
1、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8m
B
C
A
6m
解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。
解:根据勾股定理得:
AB2= 92 + 122
=81+144
=225
即:AC=15
∴AC+AB=9+15=24(米)
答:旗杆折断前有10米。
2、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
9米
12米
A
B
C
C
A.8 米 B.9 米 C.10米 D.14米
1、如图,一个长8 米,宽6 米的草地,需在相对角的顶点间加一条小路,则小路的长为 ( )
8m
6m
别踩我,我怕疼!
求下图中表示边的未知数的值.
y
144
169
求下列直角三角形中未知边的长:
12
5
x
=625
225
400
A
225
81
B
=144
求下列图中字母所表示的正方形的面积
判断题:
ABC的两边AB=5,AC=12,则BC=13 ( )
5 或
4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
D
A
B
C
1、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
提示
构造直角三角形
在Rt△ABC中,∠C=90°
(1) 已知:a=6,b=8,求c;
(2) 已知:c=13,b=5,求a;
(3) 已知: a:b=3:4,c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
由勾股定理得: c2=a2+b2
=62+82
=100
∴c=10
方法
小结
由勾股定理得: a2=c2-b2
=132-52
=144
∴c=12
设a=3k b=4k
由勾股定理得: c2=a2+b2
=9k2+16k2
=25k2
∴c=5k
又∵c=15 ∴k=3
∴a=9 b=12
a
b
c
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
弦图
现在我们一起来探索“弦图”的奥妙吧!
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
公式变形
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
