人教版初中数学八年级下册18.1.1《平行四边形性质的简单应用》课件(共22张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册18.1.1《平行四边形性质的简单应用》课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 08:32:18 | ||
图片预览


文档简介
(共22张PPT)
平行四边形的性质(1)
一、创设情境,导入课题
仔细观察下面各图中蕴含着一种什么几何图形?
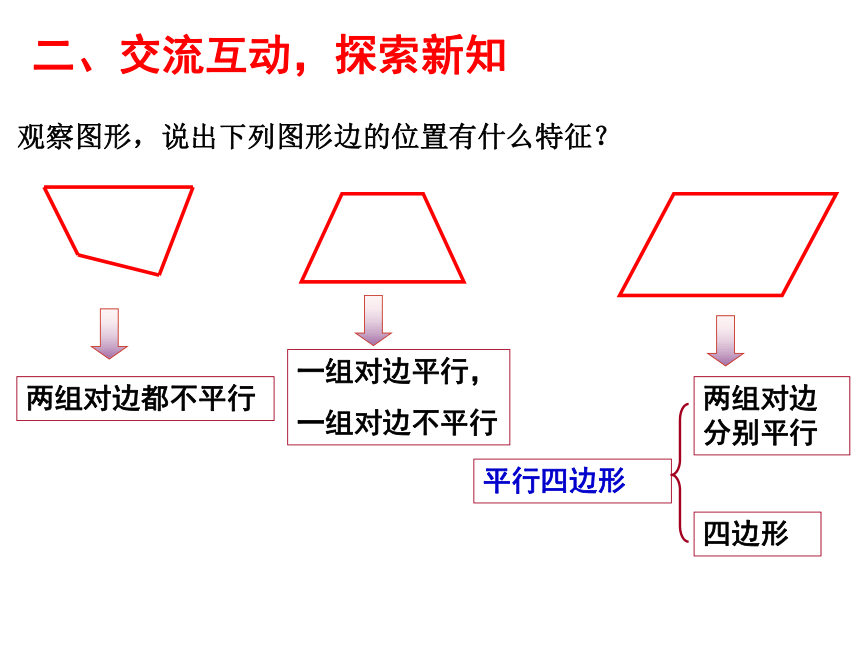
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
观察图形,说出下列图形边的位置有什么特征?
二、交流互动,探索新知
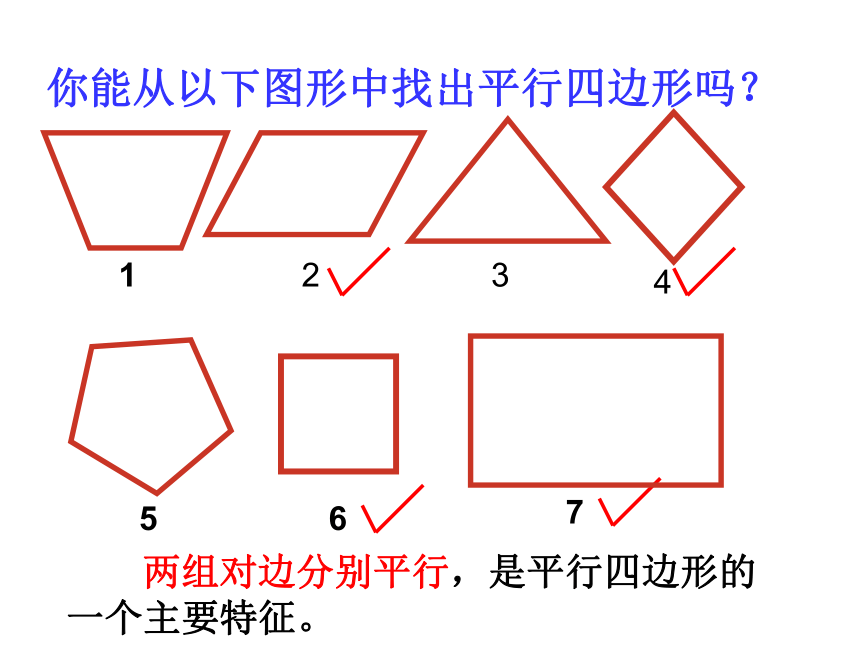
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
6
7
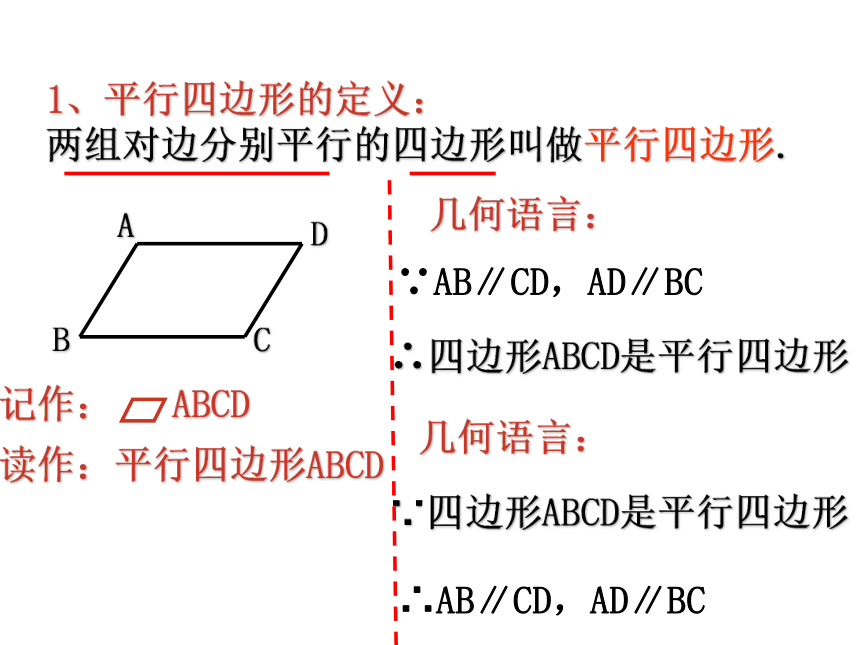
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
∴四边形ABCD是平行四边形
几何语言:
∵AB∥CD,AD∥BC
几何语言:
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
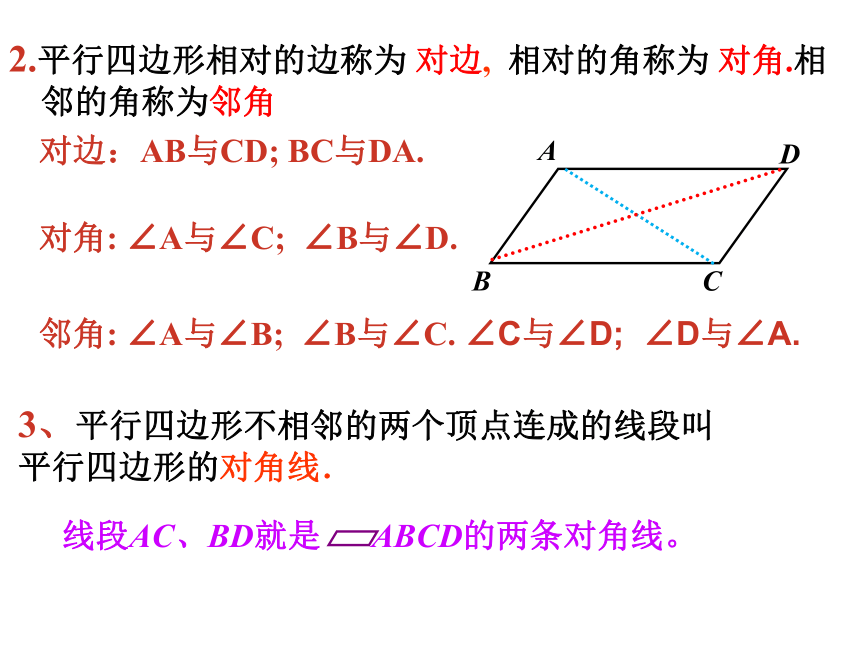
3、平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
线段AC、BD就是 ABCD的两条对角线。
A
D
C
B
2.平行四边形相对的边称为 对边, 相对的角称为 对角.相邻的角称为邻角
对边:AB与CD; BC与DA.
对角: ∠A与∠C; ∠B与∠D.
邻角: ∠A与∠B; ∠B与∠C. ∠C与∠D; ∠D与∠A.
A
B
C
D
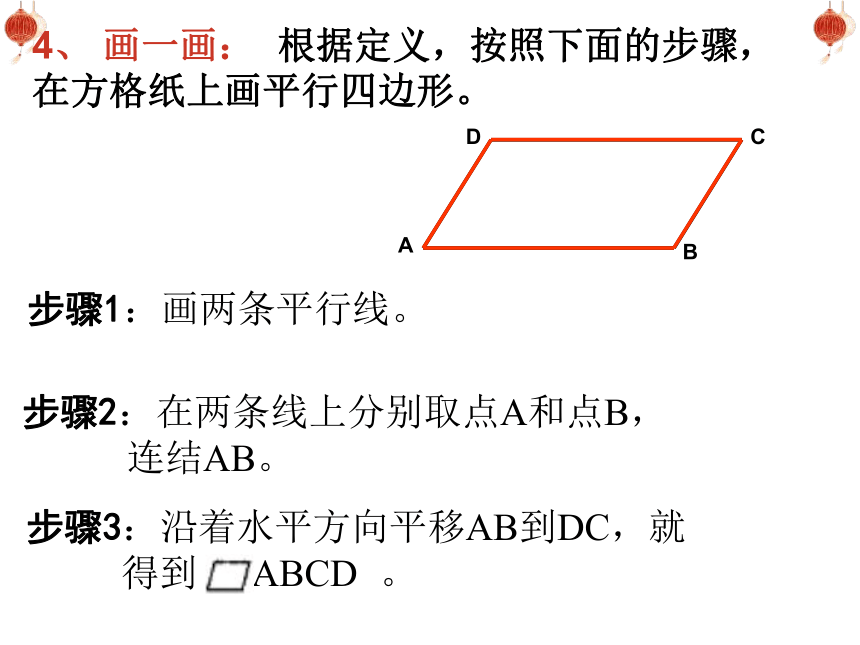
4、 画一画: 根据定义,按照下面的步骤,在方格纸上画平行四边形。
步骤1:画两条平行线。
步骤2:在两条线上分别取点A和点B,
连结AB。
步骤3:沿着水平方向平移AB到DC,就 得到 。
ABCD
A
B
D
C
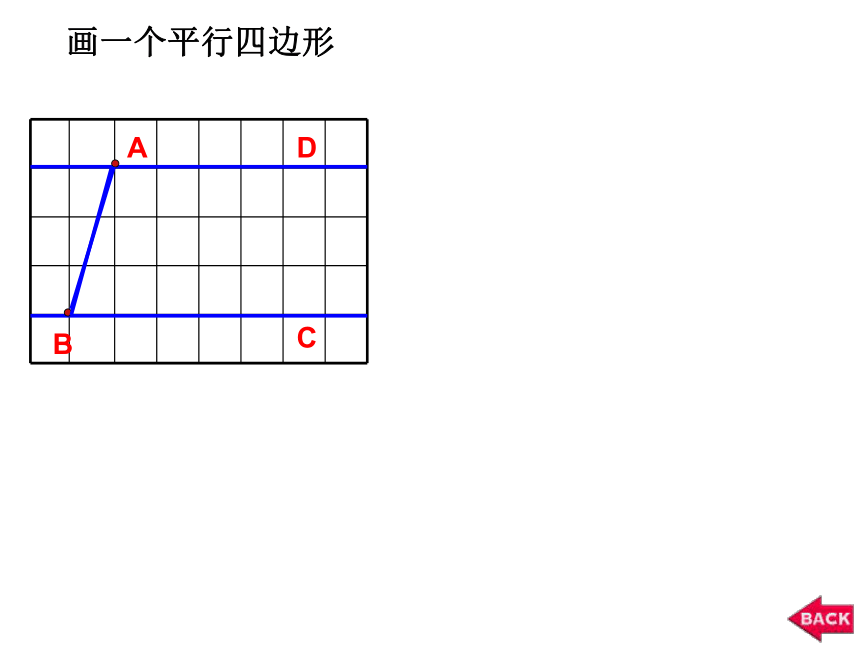
画一个平行四边形
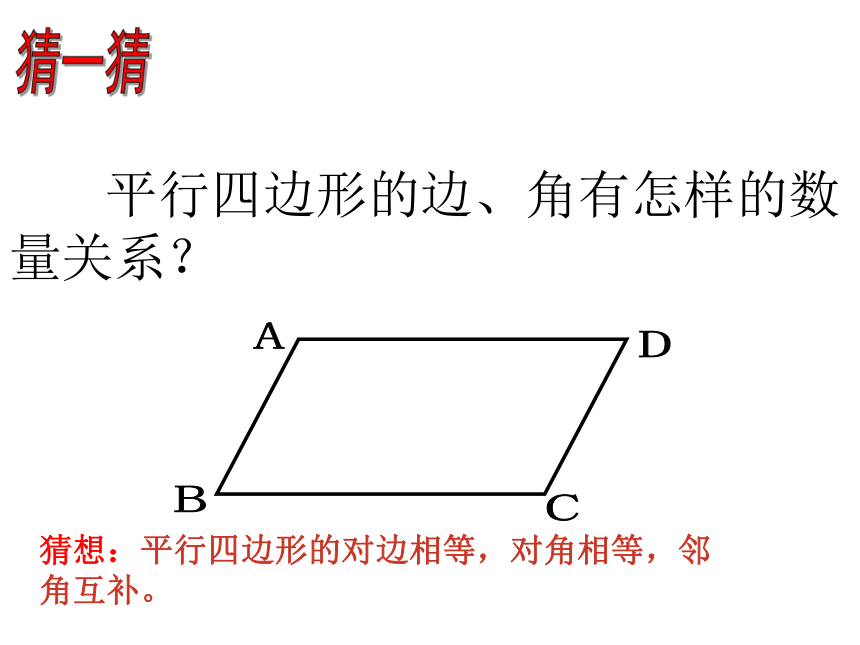
平行四边形的边、角有怎样的数量关系?
猜想:平行四边形的对边相等,对角相等,邻角互补。
6、量一量:请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,它的边、角之间有什么数量关系?是否和你的猜想一致。
7、证一证:用你以前所学的知识证明你的猜想.
猜想:平行四边形的对边相等,对角相等,邻角互补。
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
利用转化思想,把平行四边形知识,转 化为全等三角形知识,从而得到对边和对角相等。
(1)平行四边形的对边平行.
8、归纳:平行四边形边的性质
(2)平行四边形的对边相等.
∵ 在 ABCD中,
∴ AB∥CD,AD∥BC
∵ 在 ABCD中,
∴ AB=CD,AD=BC
几何语言:
几何语言:
(4)平行四边形的邻角互补.
(3)平行四边形的对角相等.
∵ 在 ABCD中,
∴ ∠A=∠ C ,∠ B =∠D,
∵ 在 ABCD中,
∴∠A+∠B=180°,∠B+∠C=180°
∠C+∠D=180°, ∠D+∠A=180°
几何语言:
几何语言:
易错点:
∠A+∠B=180°
∠B+∠C=180°
分别是哪两线平行推出的结果
如图所示,四边形ABCD是平行四边形
三、随堂练习,深化知识
1、比一比,看谁快!
(1)若∠A=70°,则∠B=
∠C= ; ∠D=
(2)若∠A+∠C=80°,
则∠A= ; ∠D= 。
70°
110°
110°
40°
140°
2.如图1, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为 cm
3.如图1,在 ABCD中,∠DAB:∠B=1:2,则∠D的度数是
8
120°
图1
4.如图2 ,若BE平分∠ABC,则ED= .
A
B
D
C
E
9cm
5cm
图2
2
3
1
5cm
5cm
4cm
4cm
DE=BF 吗?
应用知识 解决问题
例1 如图, ABCD中,DE⊥AB,BF⊥CD,垂
足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
证明:
∵ 在 ABCD中,
∴ ∠A=∠ C , AD =CB,
又∠AED =∠CFB = 90 °,
∴ △ADE≌ △CBF.
∴ AE=CF
应用知识 解决问题
例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么?
A
B
C
D
b
a
平行线间的距离
1、已知如图:E、F是平行四边形ABCD的对角线AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE (2)EB∥DF
1
2
3
4
五、延伸拓展
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
思考:从拼图可以得到什么启示?
归纳: 平行四边形是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
2、动手操作
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
平行四边形的性质对边平行
平行四边形的性质对边相等
平行四边形的性质对角相等
平行四边形的性质邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为两个全等的三角形进行解题。
六、课堂小结
布置作业:
作业:
1、教科书第43页练习第1,2题;习题18.1第1,2,7,8题。
2 思考:平行四边形的对角线有什么关系?
平行四边形的性质(1)
一、创设情境,导入课题
仔细观察下面各图中蕴含着一种什么几何图形?
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
观察图形,说出下列图形边的位置有什么特征?
二、交流互动,探索新知
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
6
7
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
∴四边形ABCD是平行四边形
几何语言:
∵AB∥CD,AD∥BC
几何语言:
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
3、平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
线段AC、BD就是 ABCD的两条对角线。
A
D
C
B
2.平行四边形相对的边称为 对边, 相对的角称为 对角.相邻的角称为邻角
对边:AB与CD; BC与DA.
对角: ∠A与∠C; ∠B与∠D.
邻角: ∠A与∠B; ∠B与∠C. ∠C与∠D; ∠D与∠A.
A
B
C
D
4、 画一画: 根据定义,按照下面的步骤,在方格纸上画平行四边形。
步骤1:画两条平行线。
步骤2:在两条线上分别取点A和点B,
连结AB。
步骤3:沿着水平方向平移AB到DC,就 得到 。
ABCD
A
B
D
C
画一个平行四边形
平行四边形的边、角有怎样的数量关系?
猜想:平行四边形的对边相等,对角相等,邻角互补。
6、量一量:请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,它的边、角之间有什么数量关系?是否和你的猜想一致。
7、证一证:用你以前所学的知识证明你的猜想.
猜想:平行四边形的对边相等,对角相等,邻角互补。
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
利用转化思想,把平行四边形知识,转 化为全等三角形知识,从而得到对边和对角相等。
(1)平行四边形的对边平行.
8、归纳:平行四边形边的性质
(2)平行四边形的对边相等.
∵ 在 ABCD中,
∴ AB∥CD,AD∥BC
∵ 在 ABCD中,
∴ AB=CD,AD=BC
几何语言:
几何语言:
(4)平行四边形的邻角互补.
(3)平行四边形的对角相等.
∵ 在 ABCD中,
∴ ∠A=∠ C ,∠ B =∠D,
∵ 在 ABCD中,
∴∠A+∠B=180°,∠B+∠C=180°
∠C+∠D=180°, ∠D+∠A=180°
几何语言:
几何语言:
易错点:
∠A+∠B=180°
∠B+∠C=180°
分别是哪两线平行推出的结果
如图所示,四边形ABCD是平行四边形
三、随堂练习,深化知识
1、比一比,看谁快!
(1)若∠A=70°,则∠B=
∠C= ; ∠D=
(2)若∠A+∠C=80°,
则∠A= ; ∠D= 。
70°
110°
110°
40°
140°
2.如图1, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为 cm
3.如图1,在 ABCD中,∠DAB:∠B=1:2,则∠D的度数是
8
120°
图1
4.如图2 ,若BE平分∠ABC,则ED= .
A
B
D
C
E
9cm
5cm
图2
2
3
1
5cm
5cm
4cm
4cm
DE=BF 吗?
应用知识 解决问题
例1 如图, ABCD中,DE⊥AB,BF⊥CD,垂
足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
证明:
∵ 在 ABCD中,
∴ ∠A=∠ C , AD =CB,
又∠AED =∠CFB = 90 °,
∴ △ADE≌ △CBF.
∴ AE=CF
应用知识 解决问题
例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么?
A
B
C
D
b
a
平行线间的距离
1、已知如图:E、F是平行四边形ABCD的对角线AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE (2)EB∥DF
1
2
3
4
五、延伸拓展
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
思考:从拼图可以得到什么启示?
归纳: 平行四边形是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
2、动手操作
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
平行四边形的性质对边平行
平行四边形的性质对边相等
平行四边形的性质对角相等
平行四边形的性质邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为两个全等的三角形进行解题。
六、课堂小结
布置作业:
作业:
1、教科书第43页练习第1,2题;习题18.1第1,2,7,8题。
2 思考:平行四边形的对角线有什么关系?
