人教版初中数学八年级下册18.1.3三角形的中位线定理课件(共15张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册18.1.3三角形的中位线定理课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 669.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:06:19 | ||
图片预览


文档简介
18.1 三角形的中位线
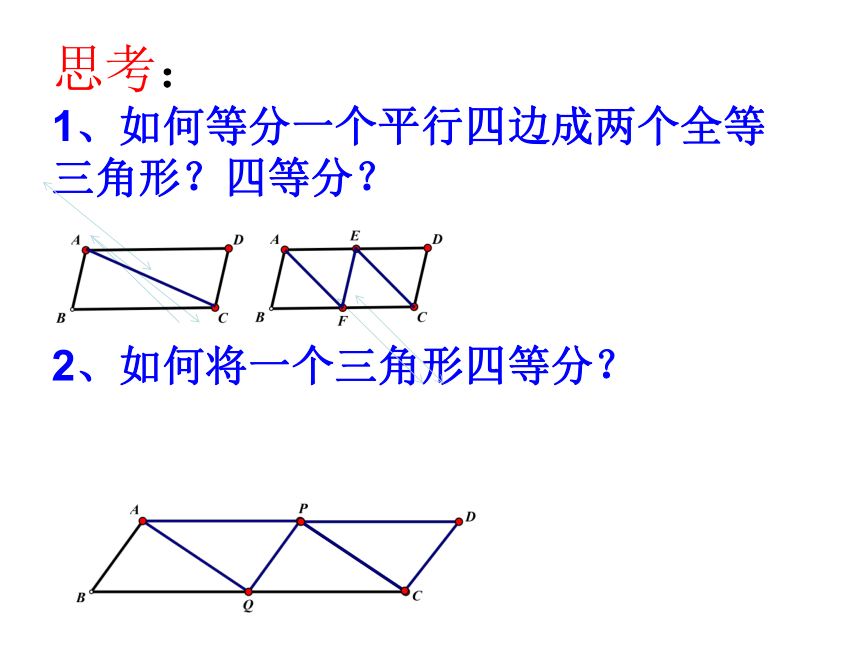
思考:
1、如何等分一个平行四边成两个全等三角形?四等分?
2、如何将一个三角形四等分?
A
B
C
D
E
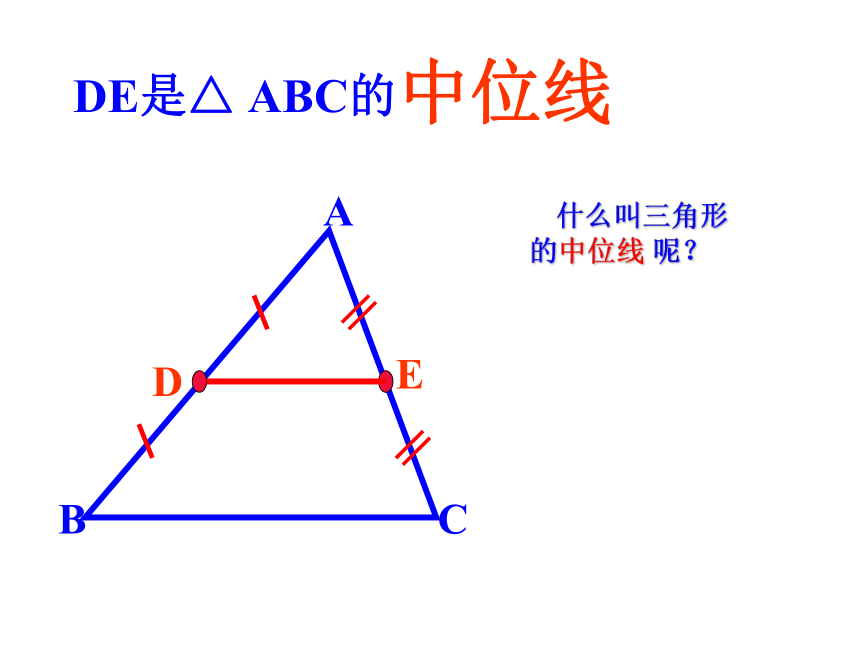
DE是△ ABC的
中位线
什么叫三角形的中位线 呢?
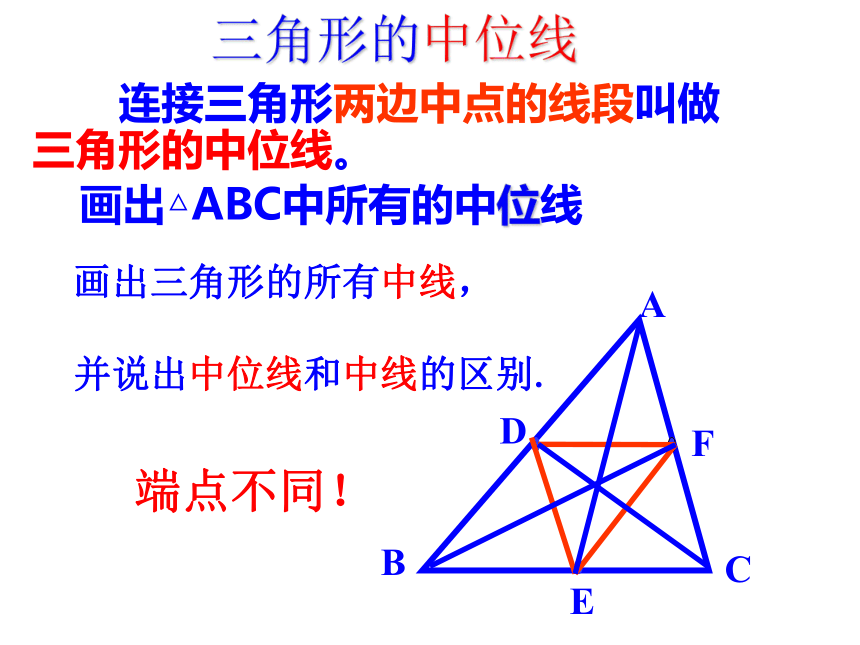
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线,
并说出中位线和中线的区别.
D
E
F
端点不同!
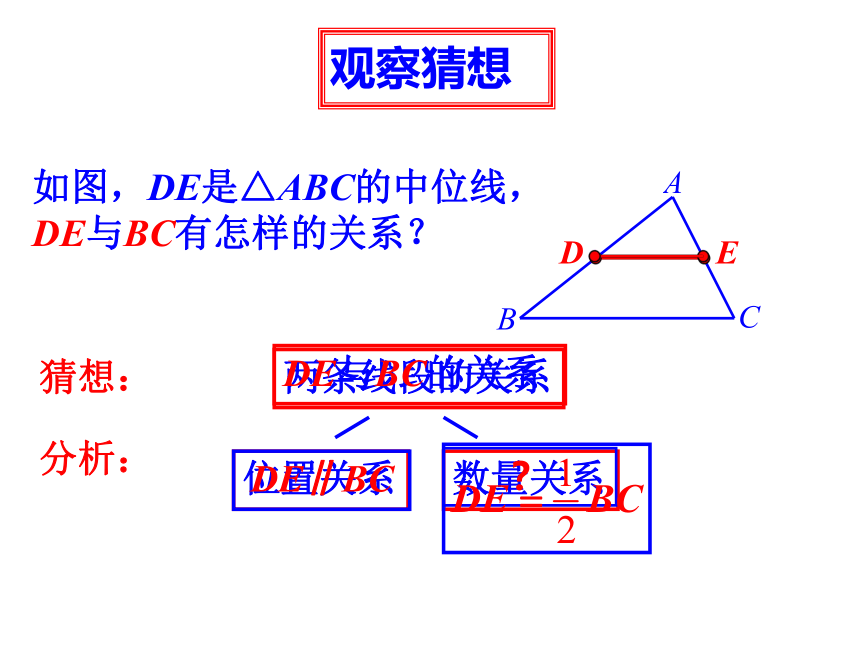
观察猜想
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
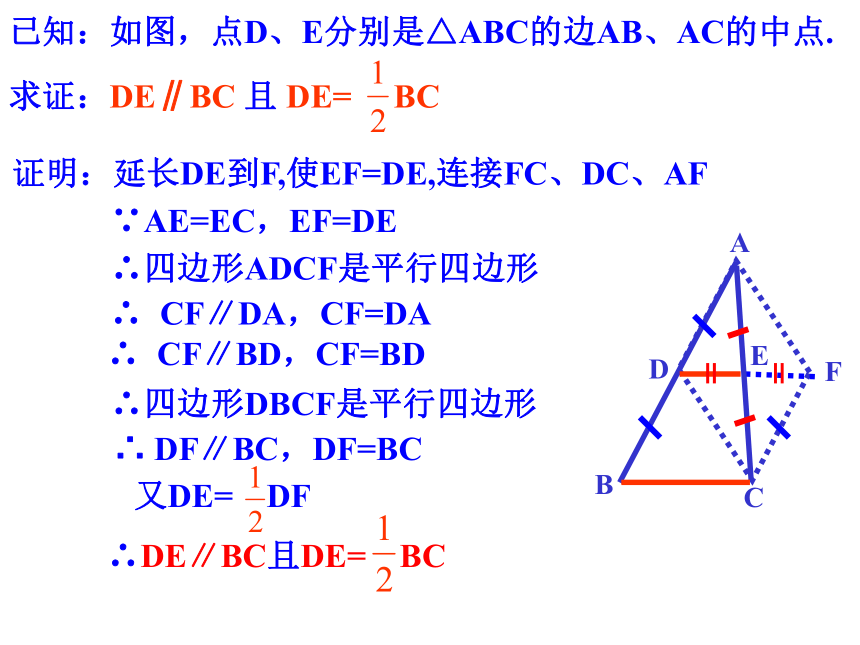
已知:如图,点D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC 且 DE= BC
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC,EF=DE
∴ CF∥DA,CF=DA
∴ CF∥BD,CF=BD
∴ DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
B
C
A
D
E
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
三角形中位线定理:
A
B
C
D
E
∵DE是△ABC的中位线,
∴DE∥BC且DE= BC
符号语言:
有何作用?
( ∵AD=BD, AE=CE )
这个定理提供了证明线段平行以及
线段成2倍关系的根据.
三角形的中位线平行且等于第三边的一半。
A
B
C
D
E
如图,D、E、F分别是△ABC的三边的中点,那么,DE、DF、EF都是△ABC的中位线。
F
DE∥BC且DE= BC
同理:DF∥AC且DF= AC;
EF∥AB且EF= AB
由此可知:……
1、如图,△ABC中,AD是BC的中线,EF是中位线,求证:AD、EF互相平分。.
A
B
C
D
E
F
2、已知: 如图,点E、F、G、H分别是四边形
ABCD各边中点。
求证:四边形EFGH为平行四边形。
证明:连接AC
∵ E、F是AB、BC边中点
∴EF∥AC且EF= AC
同理:HG ∥ AC且HG = AC
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。
E
F
G
H
A
B
C
D
(一组对边平行且相等的四边形是平行四边形)
顺次连接四边形各边中点的线段组成一个平行四边形
课堂练习
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
分别找出AC和BC的中点M、N.
若MN=36 m,则AB=
2MN=72 m
如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?
3.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你能
在图中画出多少个平行四边形?
A
B
C
D
E
F
3:如图,△ABC中,D是AB上一点,且
AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF
A
C
B
F
E
D
证明:
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)
思考
一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是多少?
思考:
1、如何等分一个平行四边成两个全等三角形?四等分?
2、如何将一个三角形四等分?
A
B
C
D
E
DE是△ ABC的
中位线
什么叫三角形的中位线 呢?
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线,
并说出中位线和中线的区别.
D
E
F
端点不同!
观察猜想
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
已知:如图,点D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC 且 DE= BC
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC,EF=DE
∴ CF∥DA,CF=DA
∴ CF∥BD,CF=BD
∴ DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
B
C
A
D
E
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
三角形中位线定理:
A
B
C
D
E
∵DE是△ABC的中位线,
∴DE∥BC且DE= BC
符号语言:
有何作用?
( ∵AD=BD, AE=CE )
这个定理提供了证明线段平行以及
线段成2倍关系的根据.
三角形的中位线平行且等于第三边的一半。
A
B
C
D
E
如图,D、E、F分别是△ABC的三边的中点,那么,DE、DF、EF都是△ABC的中位线。
F
DE∥BC且DE= BC
同理:DF∥AC且DF= AC;
EF∥AB且EF= AB
由此可知:……
1、如图,△ABC中,AD是BC的中线,EF是中位线,求证:AD、EF互相平分。.
A
B
C
D
E
F
2、已知: 如图,点E、F、G、H分别是四边形
ABCD各边中点。
求证:四边形EFGH为平行四边形。
证明:连接AC
∵ E、F是AB、BC边中点
∴EF∥AC且EF= AC
同理:HG ∥ AC且HG = AC
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。
E
F
G
H
A
B
C
D
(一组对边平行且相等的四边形是平行四边形)
顺次连接四边形各边中点的线段组成一个平行四边形
课堂练习
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
分别找出AC和BC的中点M、N.
若MN=36 m,则AB=
2MN=72 m
如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?
3.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你能
在图中画出多少个平行四边形?
A
B
C
D
E
F
3:如图,△ABC中,D是AB上一点,且
AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF
A
C
B
F
E
D
证明:
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)
思考
一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是多少?
