人教版七年级上册 第二章 整式的加减 图形变化中规律的探究课件 (共27张PPT)
文档属性
| 名称 | 人教版七年级上册 第二章 整式的加减 图形变化中规律的探究课件 (共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:16:17 | ||
图片预览



文档简介
第二章 数学活动
--图形变化中规律的探究
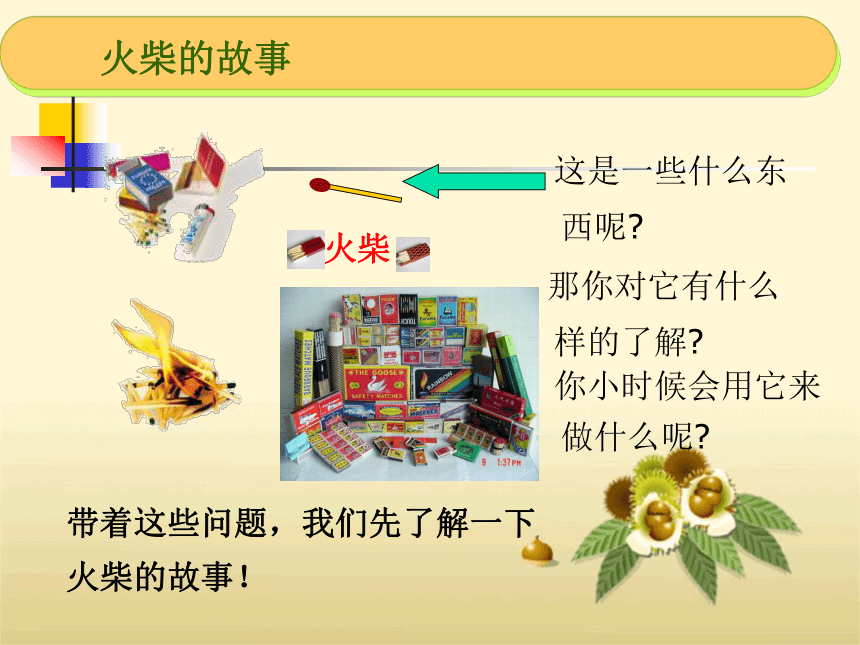
这是一些什么东
那你对它有什么
火柴
西呢?
你小时候会用它来
样的了解?
做什么呢?
带着这些问题,我们先了解一下
火柴的故事
火柴的故事!
世界上第一根火柴出现在十七世纪八十年代的法国。
直到十八世纪,意大利的威尼斯出现了一种巨型火柴,很像敲鼓的木槌,这时火柴才走进了人们的生活。那时候,这种火柴价格昂贵,只好几家合买一根。
1830年,法国人沙利埃制成一种小巧灵便的磨擦火柴。划火柴时只要在墙上、砖头上或鞋底轻轻地一擦,火柴就燃着了。然而,这种火柴会引起人中毒,而且易自燃。
1855年,瑞典人伦斯特姆设计出世界上第一盒安全火柴。这种火柴既无毒,又不会引起火灾。至今,这种火柴还在使用。
火柴除了给我们带来光亮,还
有什么另样的用途呢?带着这
个问题我们一起来看大屏幕。
火柴发展的旅途
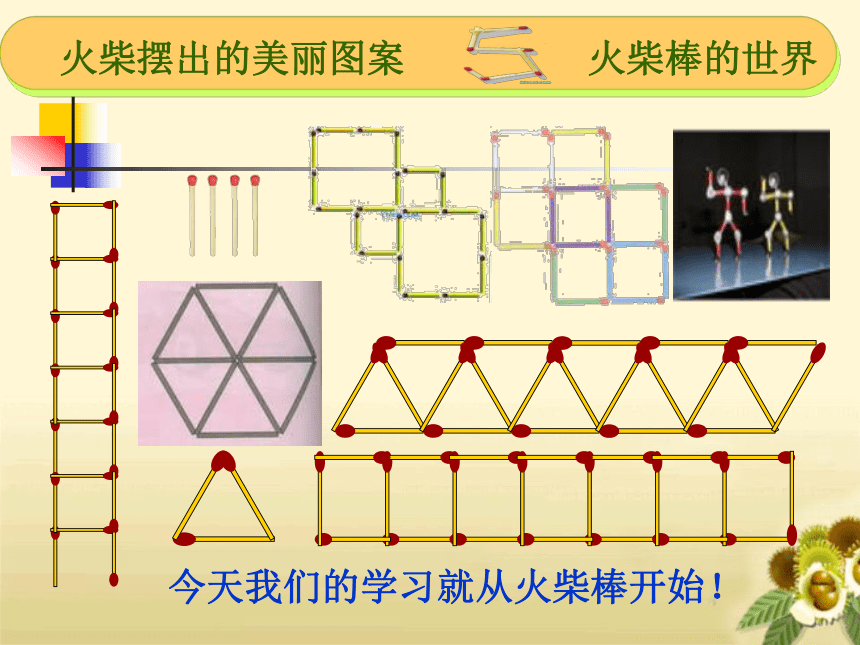
火柴摆出的美丽图案
火柴棒的世界
今天我们的学习就从火柴棒开始!
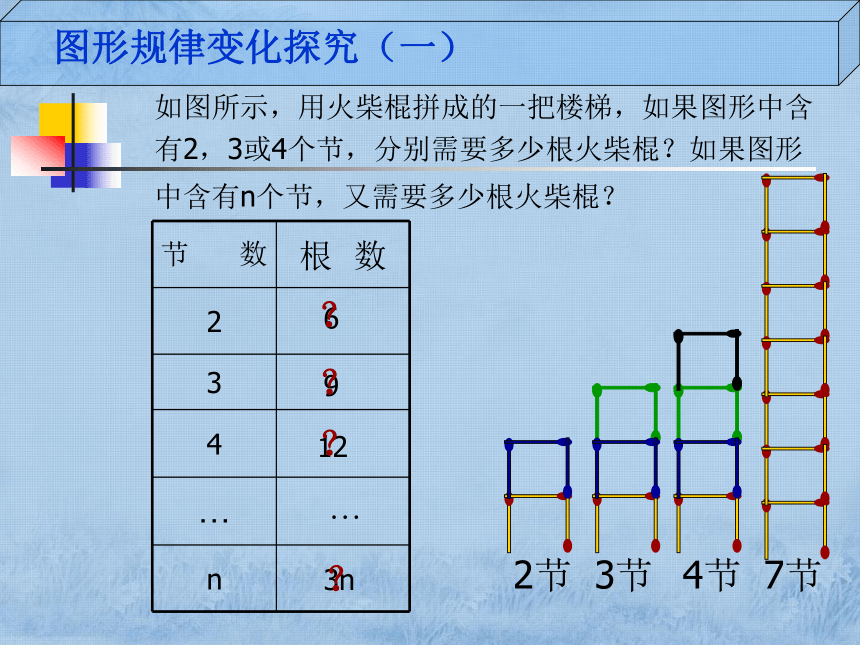
如图所示,用火柴棍拼成的一把楼梯,如果图形中含
中含有n个节,又需要多少根火柴棍?
有2,3或4个节,分别需要多少根火柴棍?如果图形
2节
3节
4节
节数
根 数
2
3
4
…
n
6
9
12
…
7节
3n
图形规律变化探究(一)
?
?
?
?
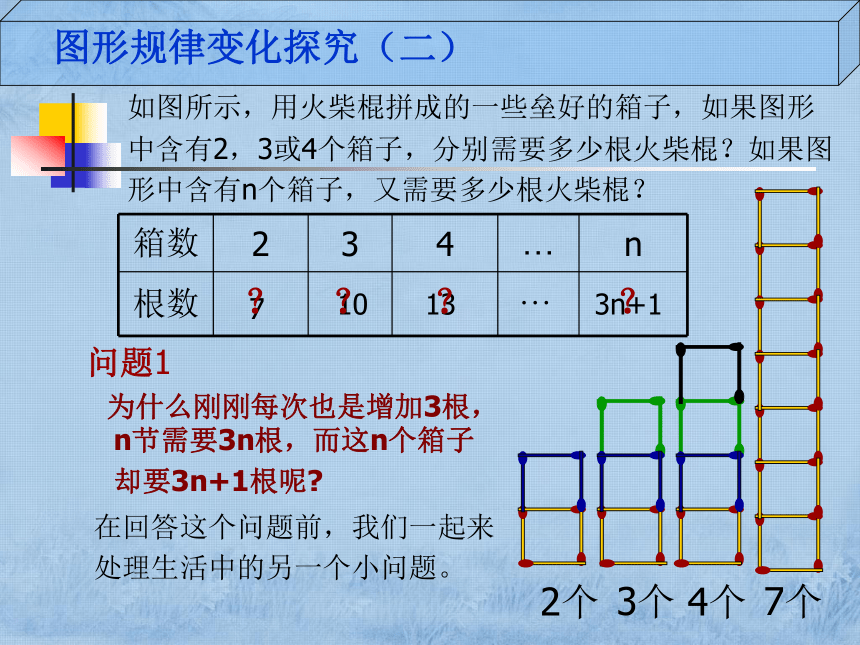
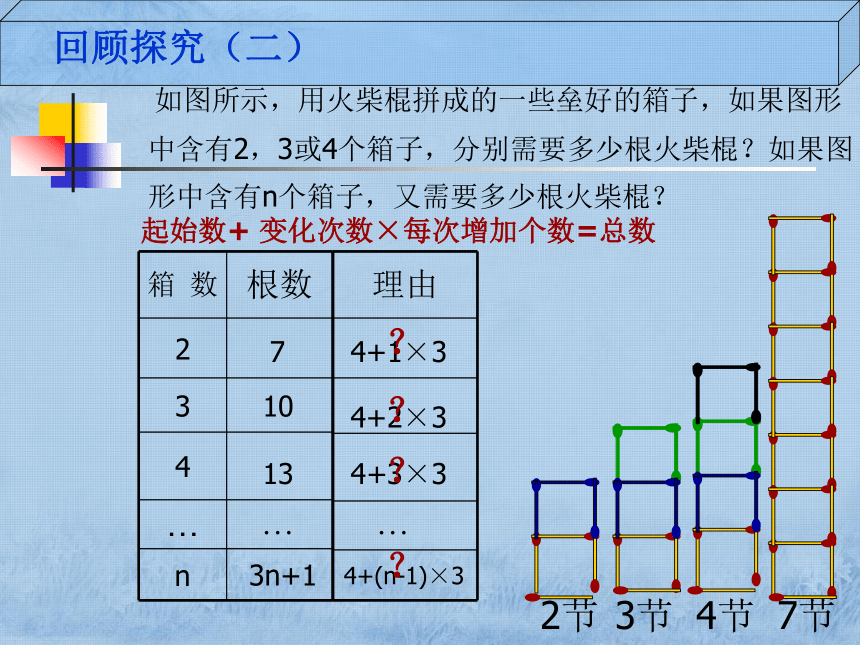
如图所示,用火柴棍拼成的一些垒好的箱子,如果图形
形中含有n个箱子,又需要多少根火柴棍?
中含有2,3或4个箱子,分别需要多少根火柴棍?如果图
2个
3个
4个
7个
箱数
2
3
4
…
n
根数
7
10
13
…
3n+1
为什么刚刚每次也是增加3根,
问题1
n节需要3n根,而这n个箱子
却要3n+1根呢?
在回答这个问题前,我们一起来
处理生活中的另一个小问题。
图形规律变化探究(二)
?
?
?
?
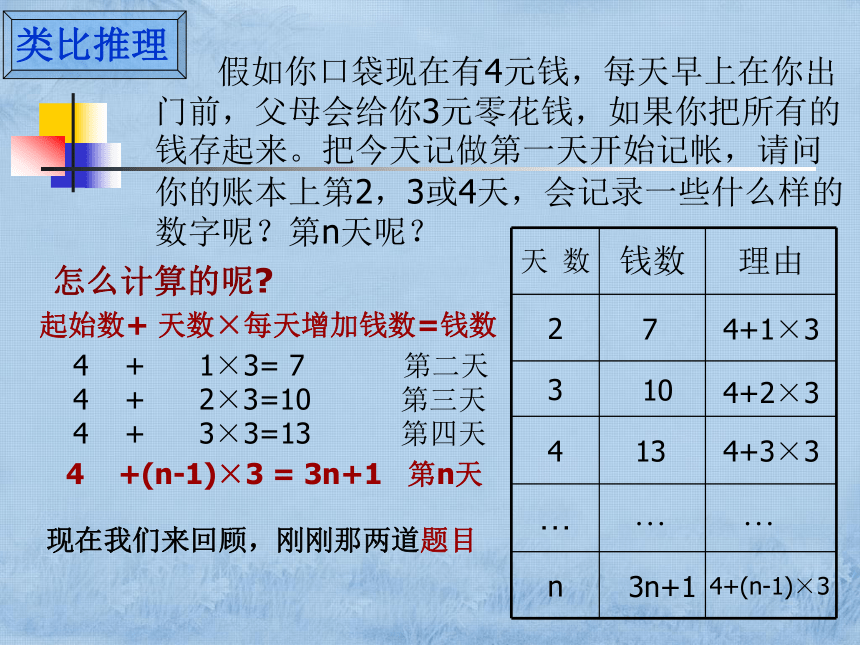
假如你口袋现在有4元钱,每天早上在你出门前,父母会给你3元零花钱,如果你把所有的钱存起来。把今天记做第一天开始记帐,请问你的账本上第2,3或4天,会记录一些什么样的数字呢?第n天呢?
怎么计算的呢?
天数
钱数
理由
2
3
4
…
n
7
10
13
…
3n+1
4+1×3
4+2×3
4+3×3
…
4+(n-1)×3
起始数+ 天数×每天增加钱数=钱数
4 +(n-1)×3 = 3n+1 第n天
现在我们来回顾,刚刚那两道题目
4 + 1×3= 7 第二天
4 + 2×3=10 第三天
4 + 3×3=13 第四天
类比推理
如图所示,用火柴棍拼成的一些垒好的箱子,如果图形
形中含有n个箱子,又需要多少根火柴棍?
中含有2,3或4个箱子,分别需要多少根火柴棍?如果图
2节
3节
4节
7节
7
10
13
…
3n+1
4+1×3
4+2×3
4+3×3
…
4+(n-1)×3
回顾探究(二)
起始数+ 变化次数×每次增加个数=总数
理由
箱数
根数
2
3
4
…
n
?
?
?
?
如图所示,用火柴棍拼成的一把楼梯,如果图形中含
中含有n个节,又需要多少根火柴棍?
有2,3或4个节,分别需要多少根火柴棍?如果图形
2节
3节
4节
节数
根数
2
6
3
9
4
12
…
…
n
3n
7节
理由
6=3+1×3
9=3+2×3
12=3+3×3
…
3n=3+(n-1)×3
回顾探究(一)
?
?
?
?
为什么楼梯每次也是增加3根,n节就是3n而
这n个箱子却是3n+1根呢?
2节
3节
4节
7节
2节
3节
4节
7节
3+(n-1)×3 = 3n
4+(n-1)×3 = 3n+1
所以我们把原因归纳
为:它们起始的根数不一样,一个是3另一个是4
起始数4根
起始数3根
回顾问题1:
当我们遇到图形有规律的变化问题时,我们
第n项=起始数+ 增加的次数×每次增加的个数
从第1副图形到第n副图形变化的次数往往是(n-1)次
可以观察图形的变化规律。然后再用数学符号将
其表达出来。例如像刚才那样的图形变换每次都
是增加相同根数的火柴,我们就可以用这样一个
表达式将其图形变化规律表达出来:
方法与经验总结
实践应用之活动3:实践是检验真知的唯一方法
如图所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2,3或4个三角形,分别需要多少根火柴棍?如果图形中含有n个三角形,需要多少根火柴棍?
我们发现每次增加的火柴棍数目都是两根,根据我们刚刚方法。
所以第n个三角形要火柴数目为:3+(n-1) ×2=2n-1
(1)
(2)
(3)
(4)
第n项=起始数+ 增加的次数×每次增加的个数
动态
演示
(1)将下表填写完整:
图形编号
1
2
3
三角形个数
(2)在第n个图形中有 个三角形(用含n的式子表示)
1
5
9
4n-3
1 2 3
如图1所示的是一个三角形,分别连接这个三角形三边的中点得到2,再分别连接图2中间的小三角形的中点,得到3,按此方法继续连接,请你根据每个图中三角形的个数的规律完成下列问题。
实践应用之活动4:实践是检验真知的唯一方法
动态
演示
?
?
?
?
解决这类推理问题的时候,首先观察
抢答游戏,大家一起来。请选题:(一个数字后面就是一道题)
1
6
2
5
9
4
3
8
7
出图像的变化规律。然后用数学语言表达
出变化规律。
精华要领:
实战演练:勇气与智慧的交融
解决这类推理问题的时候,首先观察
抢答游戏,大家一起来。请选题:(一个数字后面就是一道题)
1
6
2
5
9
4
3
8
7
出图像的变化规律。然后用数学语言表达
出变化规律。
精华要领:
实战演练:勇气与智慧的交融
观察图中给出的三个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数的变化规律,填写下表:
第1个
第2个
第3个
图形编号
1
2
3
n
点的个数
1
6
11
5n-4
趣味抢答(10分)
动态
演示
?
?
?
?
方法2
如图所示,第2008个图形中笑脸的个数是 个,第n个图形中笑脸的个数 个
第1个
第2个
第3个
2n+1
4017
趣味抢答(10分)
动态
演示
?
?
方法2
如图所示,第2008个图形中鸡蛋的个数是 个,第n个图形中鸡蛋的个数 个
第1个
第2个
第3个
2n+1
4017
趣味抢答(10分)
动态
演示
?
?
方法2
1
2
3
1
2
3
1
2
3
简单方法2:
规律:每次增加2个
第n项就是:2n+ ;
2×1+ =3
1
1
?
?
规律:每次增加2个
第n项就是:2n+ ;
2×1+ =3
1
1
?
?
规律:每次增加5个
第n项就是:5n+ ;
5×1+ =1
(-4)
(-4)
?
?
如果增加相同的数目
第n个数学规律为变数×n+?
如图所示,用棋子摆成的一列图案,每个图案中棋子的个数记为s,按此规律,n=5时,s= ,可推断出s与n的关系式为 。
n=1,s=4
n=2,s=8
n=3,s=12
20
S=4n
趣味抢答(15分)
动态
演示
?
?
如图所示,第2008个图形中笑脸的个数是 个,第n个图形中笑脸的个数 个
第1个
第2个
第3个
4n
8032
趣味抢答(15分)
动态
演示
?
?
如图所示,是一幅苹果图,请观察图形填写下表:
图形编号
苹果个数
第1行
第2行
第3行
…
第n行
1
2
4
…
2
n
趣味抢答(15分)
?
?
?
?
如图所示,用大小相等的小正方形拼大正方形,拼第1个正方形需要4个小正方形… …拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个正方形?
第1个正方形 第2个正方形 第3个正方形
答:每增加一次多一行即为n+1,并且
多一列即为n+1,总计2n+1
趣味抢答(20分)
动态
演示
某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,第7年时,树木的分枝数为 。
年份
分枝数
第1年
1
第2年
1
第3年
2
第4年
3
第5年
5
1 2 3 4 5
8
13
你能画出第6年时的图像吗?
6
第1年
第2年
第3年
第4年
第5年
第6年
趣味抢答(20分)
?
?
动态(自动)
6
第1年
第2年
第3年
第4年
第5年
第6年
演示(手动)
1、看数字之间是否有规
2、可以通过观察图像的
当我们遇到探究图形变化规律的问题时
我们应该怎么办呢?
律,可以直接得出。
变化,来发现规律,近
而用数学语言将规律表
达出来。
作业:像这样每次翻相同的倍数,
你能找到什么简单的方法吗?
(类比增加相同的数目)
谢谢再见!
--图形变化中规律的探究
这是一些什么东
那你对它有什么
火柴
西呢?
你小时候会用它来
样的了解?
做什么呢?
带着这些问题,我们先了解一下
火柴的故事
火柴的故事!
世界上第一根火柴出现在十七世纪八十年代的法国。
直到十八世纪,意大利的威尼斯出现了一种巨型火柴,很像敲鼓的木槌,这时火柴才走进了人们的生活。那时候,这种火柴价格昂贵,只好几家合买一根。
1830年,法国人沙利埃制成一种小巧灵便的磨擦火柴。划火柴时只要在墙上、砖头上或鞋底轻轻地一擦,火柴就燃着了。然而,这种火柴会引起人中毒,而且易自燃。
1855年,瑞典人伦斯特姆设计出世界上第一盒安全火柴。这种火柴既无毒,又不会引起火灾。至今,这种火柴还在使用。
火柴除了给我们带来光亮,还
有什么另样的用途呢?带着这
个问题我们一起来看大屏幕。
火柴发展的旅途
火柴摆出的美丽图案
火柴棒的世界
今天我们的学习就从火柴棒开始!
如图所示,用火柴棍拼成的一把楼梯,如果图形中含
中含有n个节,又需要多少根火柴棍?
有2,3或4个节,分别需要多少根火柴棍?如果图形
2节
3节
4节
节数
根 数
2
3
4
…
n
6
9
12
…
7节
3n
图形规律变化探究(一)
?
?
?
?
如图所示,用火柴棍拼成的一些垒好的箱子,如果图形
形中含有n个箱子,又需要多少根火柴棍?
中含有2,3或4个箱子,分别需要多少根火柴棍?如果图
2个
3个
4个
7个
箱数
2
3
4
…
n
根数
7
10
13
…
3n+1
为什么刚刚每次也是增加3根,
问题1
n节需要3n根,而这n个箱子
却要3n+1根呢?
在回答这个问题前,我们一起来
处理生活中的另一个小问题。
图形规律变化探究(二)
?
?
?
?
假如你口袋现在有4元钱,每天早上在你出门前,父母会给你3元零花钱,如果你把所有的钱存起来。把今天记做第一天开始记帐,请问你的账本上第2,3或4天,会记录一些什么样的数字呢?第n天呢?
怎么计算的呢?
天数
钱数
理由
2
3
4
…
n
7
10
13
…
3n+1
4+1×3
4+2×3
4+3×3
…
4+(n-1)×3
起始数+ 天数×每天增加钱数=钱数
4 +(n-1)×3 = 3n+1 第n天
现在我们来回顾,刚刚那两道题目
4 + 1×3= 7 第二天
4 + 2×3=10 第三天
4 + 3×3=13 第四天
类比推理
如图所示,用火柴棍拼成的一些垒好的箱子,如果图形
形中含有n个箱子,又需要多少根火柴棍?
中含有2,3或4个箱子,分别需要多少根火柴棍?如果图
2节
3节
4节
7节
7
10
13
…
3n+1
4+1×3
4+2×3
4+3×3
…
4+(n-1)×3
回顾探究(二)
起始数+ 变化次数×每次增加个数=总数
理由
箱数
根数
2
3
4
…
n
?
?
?
?
如图所示,用火柴棍拼成的一把楼梯,如果图形中含
中含有n个节,又需要多少根火柴棍?
有2,3或4个节,分别需要多少根火柴棍?如果图形
2节
3节
4节
节数
根数
2
6
3
9
4
12
…
…
n
3n
7节
理由
6=3+1×3
9=3+2×3
12=3+3×3
…
3n=3+(n-1)×3
回顾探究(一)
?
?
?
?
为什么楼梯每次也是增加3根,n节就是3n而
这n个箱子却是3n+1根呢?
2节
3节
4节
7节
2节
3节
4节
7节
3+(n-1)×3 = 3n
4+(n-1)×3 = 3n+1
所以我们把原因归纳
为:它们起始的根数不一样,一个是3另一个是4
起始数4根
起始数3根
回顾问题1:
当我们遇到图形有规律的变化问题时,我们
第n项=起始数+ 增加的次数×每次增加的个数
从第1副图形到第n副图形变化的次数往往是(n-1)次
可以观察图形的变化规律。然后再用数学符号将
其表达出来。例如像刚才那样的图形变换每次都
是增加相同根数的火柴,我们就可以用这样一个
表达式将其图形变化规律表达出来:
方法与经验总结
实践应用之活动3:实践是检验真知的唯一方法
如图所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2,3或4个三角形,分别需要多少根火柴棍?如果图形中含有n个三角形,需要多少根火柴棍?
我们发现每次增加的火柴棍数目都是两根,根据我们刚刚方法。
所以第n个三角形要火柴数目为:3+(n-1) ×2=2n-1
(1)
(2)
(3)
(4)
第n项=起始数+ 增加的次数×每次增加的个数
动态
演示
(1)将下表填写完整:
图形编号
1
2
3
三角形个数
(2)在第n个图形中有 个三角形(用含n的式子表示)
1
5
9
4n-3
1 2 3
如图1所示的是一个三角形,分别连接这个三角形三边的中点得到2,再分别连接图2中间的小三角形的中点,得到3,按此方法继续连接,请你根据每个图中三角形的个数的规律完成下列问题。
实践应用之活动4:实践是检验真知的唯一方法
动态
演示
?
?
?
?
解决这类推理问题的时候,首先观察
抢答游戏,大家一起来。请选题:(一个数字后面就是一道题)
1
6
2
5
9
4
3
8
7
出图像的变化规律。然后用数学语言表达
出变化规律。
精华要领:
实战演练:勇气与智慧的交融
解决这类推理问题的时候,首先观察
抢答游戏,大家一起来。请选题:(一个数字后面就是一道题)
1
6
2
5
9
4
3
8
7
出图像的变化规律。然后用数学语言表达
出变化规律。
精华要领:
实战演练:勇气与智慧的交融
观察图中给出的三个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数的变化规律,填写下表:
第1个
第2个
第3个
图形编号
1
2
3
n
点的个数
1
6
11
5n-4
趣味抢答(10分)
动态
演示
?
?
?
?
方法2
如图所示,第2008个图形中笑脸的个数是 个,第n个图形中笑脸的个数 个
第1个
第2个
第3个
2n+1
4017
趣味抢答(10分)
动态
演示
?
?
方法2
如图所示,第2008个图形中鸡蛋的个数是 个,第n个图形中鸡蛋的个数 个
第1个
第2个
第3个
2n+1
4017
趣味抢答(10分)
动态
演示
?
?
方法2
1
2
3
1
2
3
1
2
3
简单方法2:
规律:每次增加2个
第n项就是:2n+ ;
2×1+ =3
1
1
?
?
规律:每次增加2个
第n项就是:2n+ ;
2×1+ =3
1
1
?
?
规律:每次增加5个
第n项就是:5n+ ;
5×1+ =1
(-4)
(-4)
?
?
如果增加相同的数目
第n个数学规律为变数×n+?
如图所示,用棋子摆成的一列图案,每个图案中棋子的个数记为s,按此规律,n=5时,s= ,可推断出s与n的关系式为 。
n=1,s=4
n=2,s=8
n=3,s=12
20
S=4n
趣味抢答(15分)
动态
演示
?
?
如图所示,第2008个图形中笑脸的个数是 个,第n个图形中笑脸的个数 个
第1个
第2个
第3个
4n
8032
趣味抢答(15分)
动态
演示
?
?
如图所示,是一幅苹果图,请观察图形填写下表:
图形编号
苹果个数
第1行
第2行
第3行
…
第n行
1
2
4
…
2
n
趣味抢答(15分)
?
?
?
?
如图所示,用大小相等的小正方形拼大正方形,拼第1个正方形需要4个小正方形… …拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个正方形?
第1个正方形 第2个正方形 第3个正方形
答:每增加一次多一行即为n+1,并且
多一列即为n+1,总计2n+1
趣味抢答(20分)
动态
演示
某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,第7年时,树木的分枝数为 。
年份
分枝数
第1年
1
第2年
1
第3年
2
第4年
3
第5年
5
1 2 3 4 5
8
13
你能画出第6年时的图像吗?
6
第1年
第2年
第3年
第4年
第5年
第6年
趣味抢答(20分)
?
?
动态(自动)
6
第1年
第2年
第3年
第4年
第5年
第6年
演示(手动)
1、看数字之间是否有规
2、可以通过观察图像的
当我们遇到探究图形变化规律的问题时
我们应该怎么办呢?
律,可以直接得出。
变化,来发现规律,近
而用数学语言将规律表
达出来。
作业:像这样每次翻相同的倍数,
你能找到什么简单的方法吗?
(类比增加相同的数目)
谢谢再见!
