人教版七年级数学下册 第八章二元一次方程组 8.2.1代入消元解二元一次方程组 课件 (共24张PPT)
文档属性
| 名称 | 人教版七年级数学下册 第八章二元一次方程组 8.2.1代入消元解二元一次方程组 课件 (共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 797.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览








文档简介
8.2.1 代入消元解二元一次方程组
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
问题1:什么是二元一次方程?
问题3:什么是二元一次方程组的解。
回顾与思考
问题2:什么是二元一次方程组?
1、已知 2x-y=1,当 x=2 时
y =___
2、已知 x-3y=11,当 y=3 时
x =___
3
20
③已知 2x-y=6,当 x=2y 时
y =
④已知 3x+2y=16,当 x=2y时
y =
2
2
C
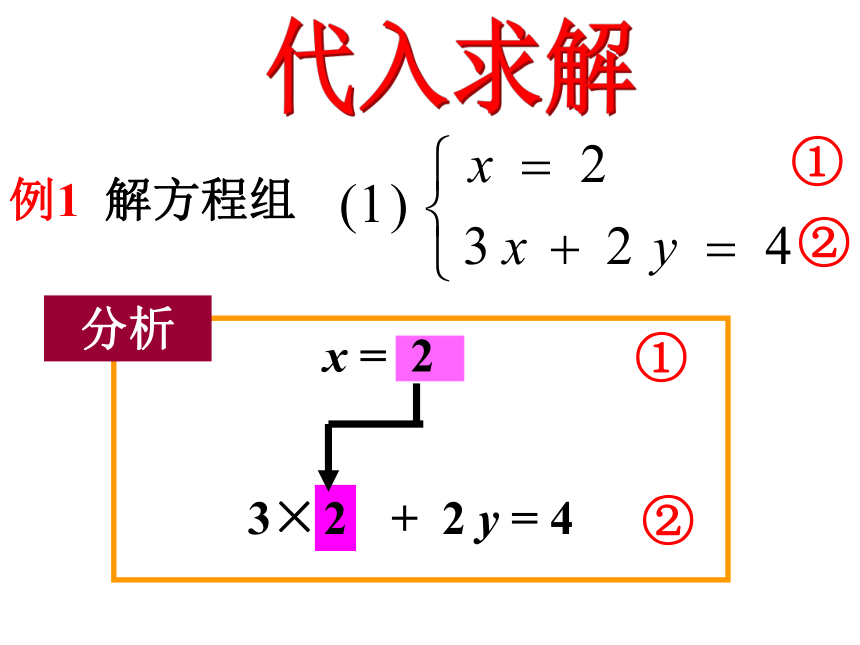
分析
①
②
3× x + 2 y = 4
x = 2
2
例1 解方程组
①
②
求二元一次方程组的解:
①
②
上面解方程组的基本思路是把“含有两个未知数”的方程转化为“只含有一个未知数”的方程。
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
将含一个未知数表示另一个未知数的代数式,代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。
这种解方程组的方法称为代入消元法,简称代入法。
“先变形,后代入,再回代,求另数”.
步骤①选择:消去未知数x,把准备
消去的x写到等号的左边。
因为③是由①变形得到的,若继续代入①,只能得到一个恒等式,不能求解。所以只能代入方程②
步骤③代入:
在方程②中,只要看到x就用(3+y)把它全部替换掉,并且把(3+y)看成一个整体加括号,从而把原方程的两个未知数,转化为一个未知数。
解方程组求:
(1)
(2)
勿忘检验
按照格式做题,既规范,又准确。
解:由题意得:
∴
C
根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
22.5吨=22.5×1000=22500千克
22500千克=22500×1000=22500000克
分析:解应用题时,单位首先要统一
y
x
数 量
250
小 瓶
500
大 瓶
总 质量
一瓶的质量
名 称
500 x
250 y
生产这种消毒液22.5吨:
500 x+250 y= 22500000
大瓶与小瓶的销售数量比为 2:5
x:y = 2:5 或者写成:5x=2y的形式
学校准备建设一个周长为60米的长方形游泳池,要求游泳池的长是宽的2倍,为了帮建筑工人计算出长和宽各是多少米?
学校的篮球比足球数的2倍少3个,篮球数与足球数的比是3∶2,求这两种球各是多少个?
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
问题1:什么是二元一次方程?
问题3:什么是二元一次方程组的解。
回顾与思考
问题2:什么是二元一次方程组?
1、已知 2x-y=1,当 x=2 时
y =___
2、已知 x-3y=11,当 y=3 时
x =___
3
20
③已知 2x-y=6,当 x=2y 时
y =
④已知 3x+2y=16,当 x=2y时
y =
2
2
C
分析
①
②
3× x + 2 y = 4
x = 2
2
例1 解方程组
①
②
求二元一次方程组的解:
①
②
上面解方程组的基本思路是把“含有两个未知数”的方程转化为“只含有一个未知数”的方程。
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
将含一个未知数表示另一个未知数的代数式,代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。
这种解方程组的方法称为代入消元法,简称代入法。
“先变形,后代入,再回代,求另数”.
步骤①选择:消去未知数x,把准备
消去的x写到等号的左边。
因为③是由①变形得到的,若继续代入①,只能得到一个恒等式,不能求解。所以只能代入方程②
步骤③代入:
在方程②中,只要看到x就用(3+y)把它全部替换掉,并且把(3+y)看成一个整体加括号,从而把原方程的两个未知数,转化为一个未知数。
解方程组求:
(1)
(2)
勿忘检验
按照格式做题,既规范,又准确。
解:由题意得:
∴
C
根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
22.5吨=22.5×1000=22500千克
22500千克=22500×1000=22500000克
分析:解应用题时,单位首先要统一
y
x
数 量
250
小 瓶
500
大 瓶
总 质量
一瓶的质量
名 称
500 x
250 y
生产这种消毒液22.5吨:
500 x+250 y= 22500000
大瓶与小瓶的销售数量比为 2:5
x:y = 2:5 或者写成:5x=2y的形式
学校准备建设一个周长为60米的长方形游泳池,要求游泳池的长是宽的2倍,为了帮建筑工人计算出长和宽各是多少米?
学校的篮球比足球数的2倍少3个,篮球数与足球数的比是3∶2,求这两种球各是多少个?
