人教版七年级数学下册8.3 实际问题与二元一次方程组(第3课时)课件(共18张PPT)
文档属性
| 名称 | 人教版七年级数学下册8.3 实际问题与二元一次方程组(第3课时)课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 751.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:16:53 | ||
图片预览




文档简介
人教版 七年级数学下册
第8章 二元一次方程组
8.3 实际问题与二元一次方程组(第3课时)
学 习 目 标
1.能够结合图表找出实际问题中的等量关系,列出方程组。
2.感受间接设未知数解决实际问题的方法,培养分析问题,
解决问题的能力,体会数形结合的思想。
用方程组解决实际问题有哪些步骤?
回 顾 旧 知
(1)设未知数,一般求什么就设什么
(2)找两个等量关系
(3)列方程组
(4)解方程组
(5)检验并做答
复 习 巩 固
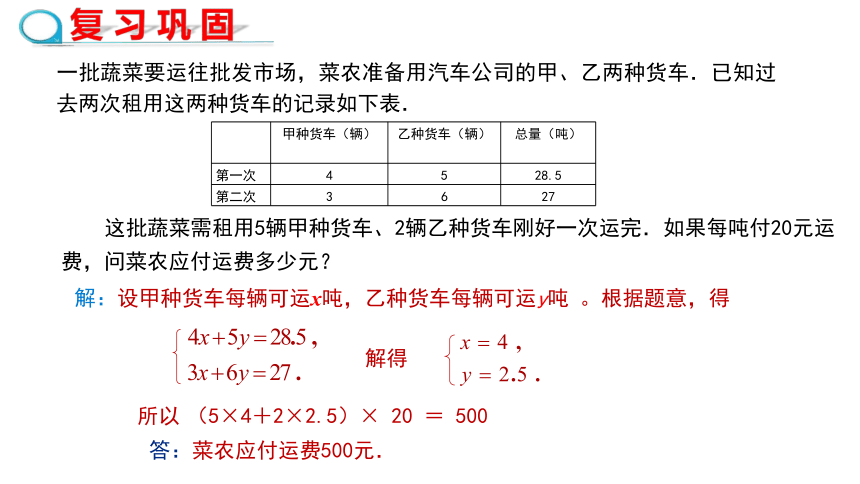
一批蔬菜要运往批发市场,菜农准备用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表.
{5940675A-B579-460E-94D1-54222C63F5DA}?
甲种货车(辆)
乙种货车(辆)
总量(吨)
第一次
4
5
28.5
第二次
3
6
27
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完.如果每吨付20元运费,问菜农应付运费多少元?
解:设甲种货车每辆可运x吨,乙种货车每辆可运y吨 。根据题意,得
解得
所以
(5×4+2×2.5)× 20 = 500
答:菜农应付运费500元.
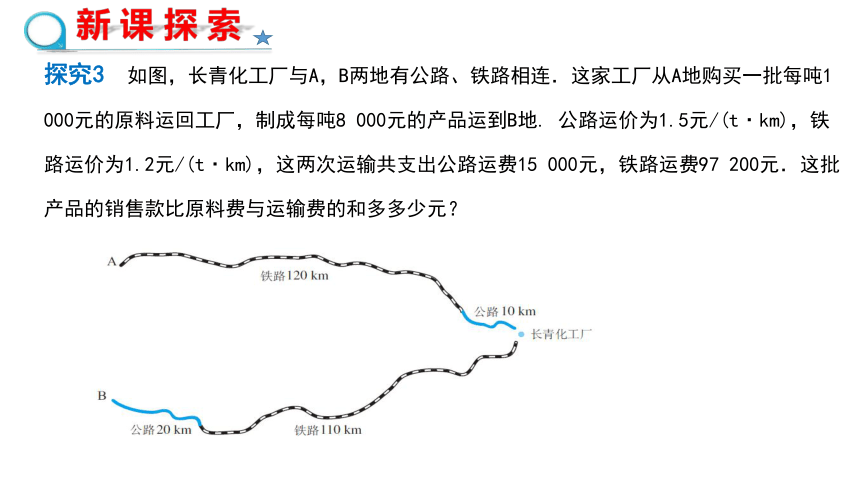
探究3 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
新 课 探 索
思 考
问题1 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km)是什
么意思?
如:把2吨货物从A地运到100千米外的B地,
经公路运输需要支付:
公路运价:经公路运输1吨货物行驶1千米需1.5元
铁路运价:经铁路运输1吨货物行驶1千米需1.2元
1.5×2×100=300元,
1.2×2×100=240元
运输费 = 运价 × 质量 × 路程
经铁路运输需要支付:
思 考
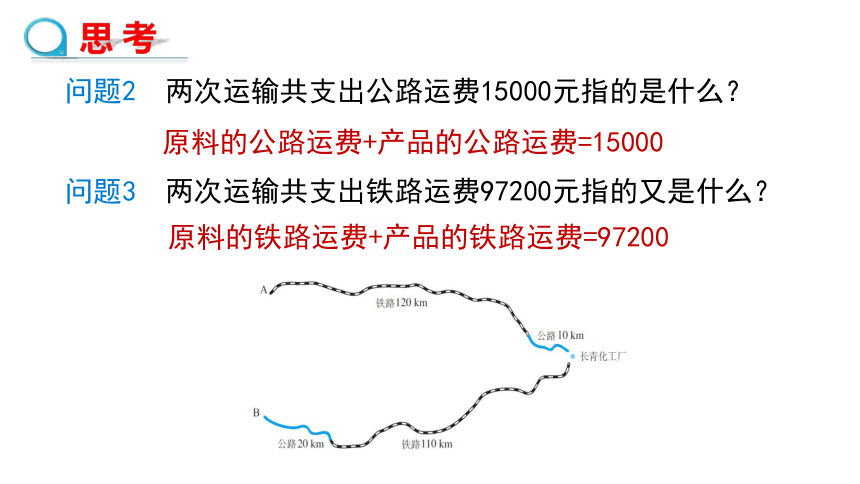
问题2 两次运输共支出公路运费15000元指的是什么?
原料的公路运费+产品的公路运费=15000
问题3 两次运输共支出铁路运费97200元指的又是什么?
原料的铁路运费+产品的铁路运费=97200
思 考
问题4 这道题求的是什么?
这批产品的销售款比原料费与运输费的和多多少元?
问题5 要解决这个问题我们必须先知道什么?
销售款 原料费 运输费
销售款=产品单价×产品数量
原料费=原料单价×原料数量
运输费=铁路运费+公路运费
图 例 分 析
设产品为x吨,原料为y吨。
1.2·y ·120
1.5·y·10
1.5·x ·20
1.2·x ·110
运输费 = 运价 × 质量 × 路程
表 格 整 理
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
1.5×20x
1.5×10y
15000
1.2×110x
1.2×120y
97200
8000x
1000y
设产品为 x 吨,原料为 y 吨。
解:设产品为x吨,原料为y吨,由题意得
解 题 过 程
解得:
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
当直接设未知数无法列出方程时,考虑间接设未知数.
归 纳 总 结
(1)在什么情况下间接设未知数?
(2)如何解决信息量较大的实际问题?
可以借助表格或者图例解决问题
(3)解决实际问题的基本过程
实际问题
归 纳 总 结
设未知数、列方程(组)
数学问题
二元一次方程组
解方程
(组)
数学问题的解
二元一次方程组的解
检 验
实际问题的答案
建模
跟 踪 训 练
1.为引导公民节约用水,合理利用资源,各地采用了价格调控等手段。某地规定如下用水收费标准:每户每月用水不超过10吨,每吨按a元收费;如果超过10吨,超过的部分每吨按b元收费,小颖家7、8月份的用水记录如下:
根据以上信息,你能求出a、b的值吗?
{5940675A-B579-460E-94D1-54222C63F5DA}月 份
用水量(吨)
水费(元)
7
12
15
8
16
21
解:根据题意,得
10a+2b = 15
10a+6b = 21
解得
a = 1.2
b = 1.5
答:a = 1.2 , b = 1.5
跟 踪 训 练
2.某果品公司通往甲、乙两地都要经过水路和陆路,这家公司从甲地购进一批水果运回公司加工成果汁再销往乙地,已知水路、陆路的运价及里程数如下表,若这两次运输支出水路运费10000元,陆路运费8000元,问该公司运进水果和运出果汁各多少吨?
{5940675A-B579-460E-94D1-54222C63F5DA}?
水路
陆路
从甲地到公司(千米)
20
30
从公司到乙地(千米)
10
40
运价:元/(吨·千米)
2
1
分析:设运进水果x吨,运出果汁y吨
解得
{5940675A-B579-460E-94D1-54222C63F5DA}?
水路运费
陆路运费
从甲地到公司
从公司到乙地
2 x·20
30x
2 y·10
40y
解:设该公司运进水果x吨,运出果汁y 吨,则
2 x·20+2 y·10 = 10000
30 x+40 y = 8000
解得
x = 240
y = 20
答:该公司运进水果240吨,运出果汁20吨。
跟 踪 训 练
3. 用1块A型钢板可制成2块C型钢板、1块D型钢板;用1块B型钢板可制成1块C型钢板、2块D型钢板。现需15块C型钢板、18块D型钢板,可恰好用A型钢板、B型钢板各多少块?
{5940675A-B579-460E-94D1-54222C63F5DA}?
A型钢板(x块)
B型钢板(y块)
总量
C型钢板
D型钢板
列表分析:设恰好用A型钢板x块、B型钢板y块,
解:设恰好用A型钢板x块、B型钢板y块,则
2x + y = 15
x + 2y = 18
解得
x = 4
y = 7
答:恰好用A型钢板4块、B型钢板7块。
2x
x
y
2y
15
18
课 堂 小 结
1. 掌握间接设未知数解决问题的方法
2. 在解决数量关系比较复杂的问题时,可借助
图例或表格对相关信息进行分类整理
3. 掌握解决实际问题的建模思想
布 置 作 业
教材102页: 5题 (必做)
8题 (选做)
第8章 二元一次方程组
8.3 实际问题与二元一次方程组(第3课时)
学 习 目 标
1.能够结合图表找出实际问题中的等量关系,列出方程组。
2.感受间接设未知数解决实际问题的方法,培养分析问题,
解决问题的能力,体会数形结合的思想。
用方程组解决实际问题有哪些步骤?
回 顾 旧 知
(1)设未知数,一般求什么就设什么
(2)找两个等量关系
(3)列方程组
(4)解方程组
(5)检验并做答
复 习 巩 固
一批蔬菜要运往批发市场,菜农准备用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表.
{5940675A-B579-460E-94D1-54222C63F5DA}?
甲种货车(辆)
乙种货车(辆)
总量(吨)
第一次
4
5
28.5
第二次
3
6
27
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完.如果每吨付20元运费,问菜农应付运费多少元?
解:设甲种货车每辆可运x吨,乙种货车每辆可运y吨 。根据题意,得
解得
所以
(5×4+2×2.5)× 20 = 500
答:菜农应付运费500元.
探究3 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
新 课 探 索
思 考
问题1 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km)是什
么意思?
如:把2吨货物从A地运到100千米外的B地,
经公路运输需要支付:
公路运价:经公路运输1吨货物行驶1千米需1.5元
铁路运价:经铁路运输1吨货物行驶1千米需1.2元
1.5×2×100=300元,
1.2×2×100=240元
运输费 = 运价 × 质量 × 路程
经铁路运输需要支付:
思 考
问题2 两次运输共支出公路运费15000元指的是什么?
原料的公路运费+产品的公路运费=15000
问题3 两次运输共支出铁路运费97200元指的又是什么?
原料的铁路运费+产品的铁路运费=97200
思 考
问题4 这道题求的是什么?
这批产品的销售款比原料费与运输费的和多多少元?
问题5 要解决这个问题我们必须先知道什么?
销售款 原料费 运输费
销售款=产品单价×产品数量
原料费=原料单价×原料数量
运输费=铁路运费+公路运费
图 例 分 析
设产品为x吨,原料为y吨。
1.2·y ·120
1.5·y·10
1.5·x ·20
1.2·x ·110
运输费 = 运价 × 质量 × 路程
表 格 整 理
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
1.5×20x
1.5×10y
15000
1.2×110x
1.2×120y
97200
8000x
1000y
设产品为 x 吨,原料为 y 吨。
解:设产品为x吨,原料为y吨,由题意得
解 题 过 程
解得:
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
当直接设未知数无法列出方程时,考虑间接设未知数.
归 纳 总 结
(1)在什么情况下间接设未知数?
(2)如何解决信息量较大的实际问题?
可以借助表格或者图例解决问题
(3)解决实际问题的基本过程
实际问题
归 纳 总 结
设未知数、列方程(组)
数学问题
二元一次方程组
解方程
(组)
数学问题的解
二元一次方程组的解
检 验
实际问题的答案
建模
跟 踪 训 练
1.为引导公民节约用水,合理利用资源,各地采用了价格调控等手段。某地规定如下用水收费标准:每户每月用水不超过10吨,每吨按a元收费;如果超过10吨,超过的部分每吨按b元收费,小颖家7、8月份的用水记录如下:
根据以上信息,你能求出a、b的值吗?
{5940675A-B579-460E-94D1-54222C63F5DA}月 份
用水量(吨)
水费(元)
7
12
15
8
16
21
解:根据题意,得
10a+2b = 15
10a+6b = 21
解得
a = 1.2
b = 1.5
答:a = 1.2 , b = 1.5
跟 踪 训 练
2.某果品公司通往甲、乙两地都要经过水路和陆路,这家公司从甲地购进一批水果运回公司加工成果汁再销往乙地,已知水路、陆路的运价及里程数如下表,若这两次运输支出水路运费10000元,陆路运费8000元,问该公司运进水果和运出果汁各多少吨?
{5940675A-B579-460E-94D1-54222C63F5DA}?
水路
陆路
从甲地到公司(千米)
20
30
从公司到乙地(千米)
10
40
运价:元/(吨·千米)
2
1
分析:设运进水果x吨,运出果汁y吨
解得
{5940675A-B579-460E-94D1-54222C63F5DA}?
水路运费
陆路运费
从甲地到公司
从公司到乙地
2 x·20
30x
2 y·10
40y
解:设该公司运进水果x吨,运出果汁y 吨,则
2 x·20+2 y·10 = 10000
30 x+40 y = 8000
解得
x = 240
y = 20
答:该公司运进水果240吨,运出果汁20吨。
跟 踪 训 练
3. 用1块A型钢板可制成2块C型钢板、1块D型钢板;用1块B型钢板可制成1块C型钢板、2块D型钢板。现需15块C型钢板、18块D型钢板,可恰好用A型钢板、B型钢板各多少块?
{5940675A-B579-460E-94D1-54222C63F5DA}?
A型钢板(x块)
B型钢板(y块)
总量
C型钢板
D型钢板
列表分析:设恰好用A型钢板x块、B型钢板y块,
解:设恰好用A型钢板x块、B型钢板y块,则
2x + y = 15
x + 2y = 18
解得
x = 4
y = 7
答:恰好用A型钢板4块、B型钢板7块。
2x
x
y
2y
15
18
课 堂 小 结
1. 掌握间接设未知数解决问题的方法
2. 在解决数量关系比较复杂的问题时,可借助
图例或表格对相关信息进行分类整理
3. 掌握解决实际问题的建模思想
布 置 作 业
教材102页: 5题 (必做)
8题 (选做)
