人教版七年级数学下册课件:7.1.2平面直角坐标系 (共16张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:7.1.2平面直角坐标系 (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 08:34:20 | ||
图片预览






文档简介
7.1.2平面直角坐标系
下图是一条数轴,我们知道,数轴上的点可以用一个实数来表示,这个实数叫做这个点的坐标。例如,点A在数轴上的坐标为-
4,点B在数轴上的坐标是2。反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了。
B
1
2
3
4
-4
A
0
-3
-2
-1
思考
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(例如下图中A、B、C、D各点)?
A
C
B
D
-3
-2
-1
0
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上为正方向;它们统称为坐标轴。两坐标轴的交点为平面直角坐标系的原点。
如图,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.也简称为直角坐标系。
y
1
3
2
-2
-1
-3
-3
-2
-1
0
1
2
3
x
坐标轴上的点不属于任何象限。
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ
四个部分,分别叫做第一象限,第二象限、第三象限和第四象限。
Ⅰ
Ⅳ
Ⅲ
Ⅱ
第四象限
第一象限
第三象限
第二象限
X
O
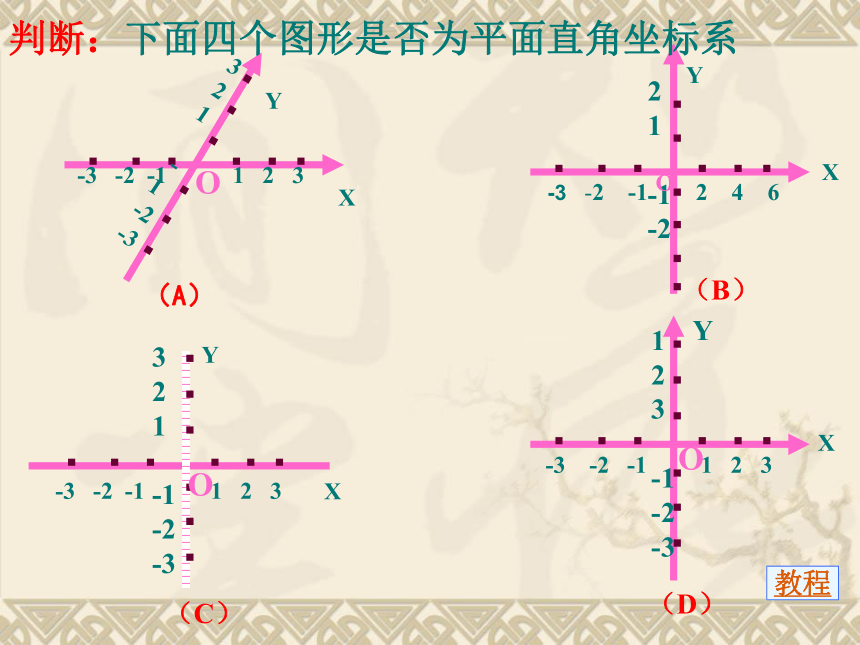
判断:下面四个图形是否为平面直角坐标系
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
教程
-3
-2
-1
2
4
6
X
Y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
1
2
3
-1
-2
-3
Y
(D)
O
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了。由点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是2,垂足N在y轴上的坐标是3,我们说点A的横坐标是2,纵坐标是3,有序数对(2,3)就叫做点A的坐标,记作A(2,3)。类似地,点B、C、D的坐标为B(
,
),C
(
,
),
D
(
,
)。
-3
-2
-1
0
1
2
3
x
点A的横坐标是2,纵坐标是3,有序数对(2,3)就叫做点A的坐标,记作A(2,3)。横坐标在前,用逗号隔开
点B,C,D,E,F的坐标为:
B(
,
),C(
,
),
D(
2,
-2)。
2
-1
-3
-3
E
F
E(
0
,-2)
F(
-3,0)
y
1
3
2
-2
-1
-3
A
B
D
C
思考
原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?
原点O的坐标是:
X轴上的点的坐标特点:
y轴上的点的坐标特点:
(0,0)
纵坐标为0。
横坐标为0。
几个象限内点的特点
第一象限:
(+,+)
第二象限:
(-,+)
第三象限:
(-,-)
第四象限:
(+,-)
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了。反之,知道了一个有序数对,你可以确定它在平面直角坐标系中的位置吗?
例题讲解
D
C
B
A
例
在平面直角坐标系中描出下列各点:
A(4,5),
B(-
2,3),
C(-
4,-1),D(2.5,-2),E(0,-4)。
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
例
在平面直角坐标系中描出下列各点:
A(4,5),
B(-
2,3),
C(-
4,-1),D(2.5,-2),E(0,-4)。
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
如上图,要描出点A(4,5)。应先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A。类似地,可以描出其他各点。
小结
1,这节课主要学面直角坐标系的有关概念,掌握了坐标平面内的点与有序数对是一一对应的。
2,会由坐标系上的点写出其坐标,会根据坐标在直角坐标系中描出对应的点。
3,掌握x轴,y轴上。象限内点的坐标的特点
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限(+,
+)第二象限:(—,
+)
第三象限(—,—)第四象限:(+,
—)
小结
作业
第70页:5、8
希望同学们取得进步!
下图是一条数轴,我们知道,数轴上的点可以用一个实数来表示,这个实数叫做这个点的坐标。例如,点A在数轴上的坐标为-
4,点B在数轴上的坐标是2。反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了。
B
1
2
3
4
-4
A
0
-3
-2
-1
思考
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(例如下图中A、B、C、D各点)?
A
C
B
D
-3
-2
-1
0
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上为正方向;它们统称为坐标轴。两坐标轴的交点为平面直角坐标系的原点。
如图,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.也简称为直角坐标系。
y
1
3
2
-2
-1
-3
-3
-2
-1
0
1
2
3
x
坐标轴上的点不属于任何象限。
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ
四个部分,分别叫做第一象限,第二象限、第三象限和第四象限。
Ⅰ
Ⅳ
Ⅲ
Ⅱ
第四象限
第一象限
第三象限
第二象限
X
O
判断:下面四个图形是否为平面直角坐标系
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
教程
-3
-2
-1
2
4
6
X
Y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
1
2
3
-1
-2
-3
Y
(D)
O
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了。由点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是2,垂足N在y轴上的坐标是3,我们说点A的横坐标是2,纵坐标是3,有序数对(2,3)就叫做点A的坐标,记作A(2,3)。类似地,点B、C、D的坐标为B(
,
),C
(
,
),
D
(
,
)。
-3
-2
-1
0
1
2
3
x
点A的横坐标是2,纵坐标是3,有序数对(2,3)就叫做点A的坐标,记作A(2,3)。横坐标在前,用逗号隔开
点B,C,D,E,F的坐标为:
B(
,
),C(
,
),
D(
2,
-2)。
2
-1
-3
-3
E
F
E(
0
,-2)
F(
-3,0)
y
1
3
2
-2
-1
-3
A
B
D
C
思考
原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?
原点O的坐标是:
X轴上的点的坐标特点:
y轴上的点的坐标特点:
(0,0)
纵坐标为0。
横坐标为0。
几个象限内点的特点
第一象限:
(+,+)
第二象限:
(-,+)
第三象限:
(-,-)
第四象限:
(+,-)
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了。反之,知道了一个有序数对,你可以确定它在平面直角坐标系中的位置吗?
例题讲解
D
C
B
A
例
在平面直角坐标系中描出下列各点:
A(4,5),
B(-
2,3),
C(-
4,-1),D(2.5,-2),E(0,-4)。
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
例
在平面直角坐标系中描出下列各点:
A(4,5),
B(-
2,3),
C(-
4,-1),D(2.5,-2),E(0,-4)。
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
如上图,要描出点A(4,5)。应先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A。类似地,可以描出其他各点。
小结
1,这节课主要学面直角坐标系的有关概念,掌握了坐标平面内的点与有序数对是一一对应的。
2,会由坐标系上的点写出其坐标,会根据坐标在直角坐标系中描出对应的点。
3,掌握x轴,y轴上。象限内点的坐标的特点
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限(+,
+)第二象限:(—,
+)
第三象限(—,—)第四象限:(+,
—)
小结
作业
第70页:5、8
希望同学们取得进步!
