人教版七年级下册8.3实际问题与二元一次方程组第三课时(共20张PPT)
文档属性
| 名称 | 人教版七年级下册8.3实际问题与二元一次方程组第三课时(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览




文档简介
8.3 实际问题与二元一次方程组
(第3课时)
学习目标:
能分析“探究3”中的数量关系,会设间接未知数,列方程组并求解,得到实际问题的答案,体会数学建模思想.
学习重点:
分析复杂问题中的数量关系,建立方程组 .
学习目标与重点
探究3
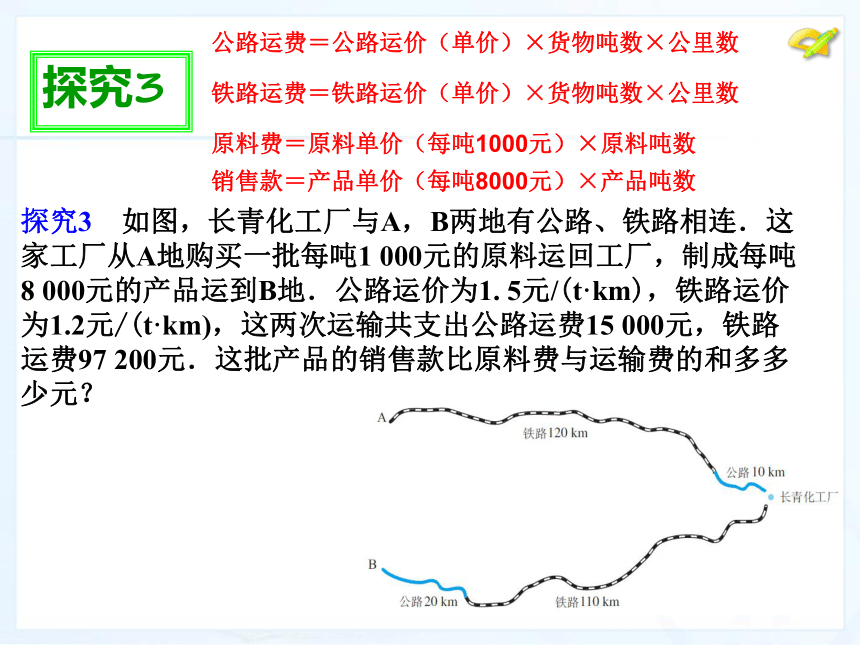
探究3 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
公路运费=公路运价(单价)×货物吨数×公里数
铁路运费=铁路运价(单价)×货物吨数×公里数
原料费=原料单价(每吨1000元)×原料吨数
销售款=产品单价(每吨8000元)×产品吨数
探究3
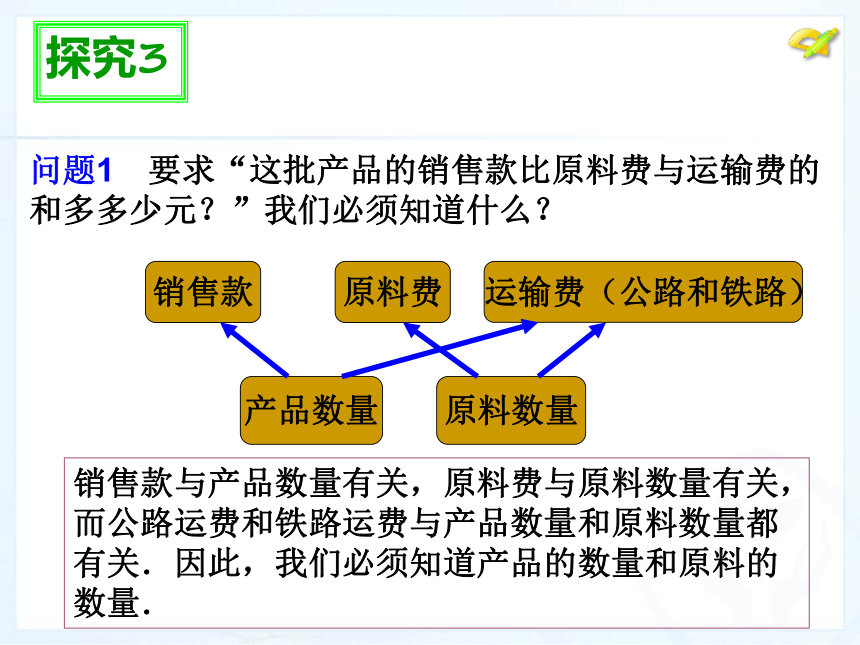
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
探究3
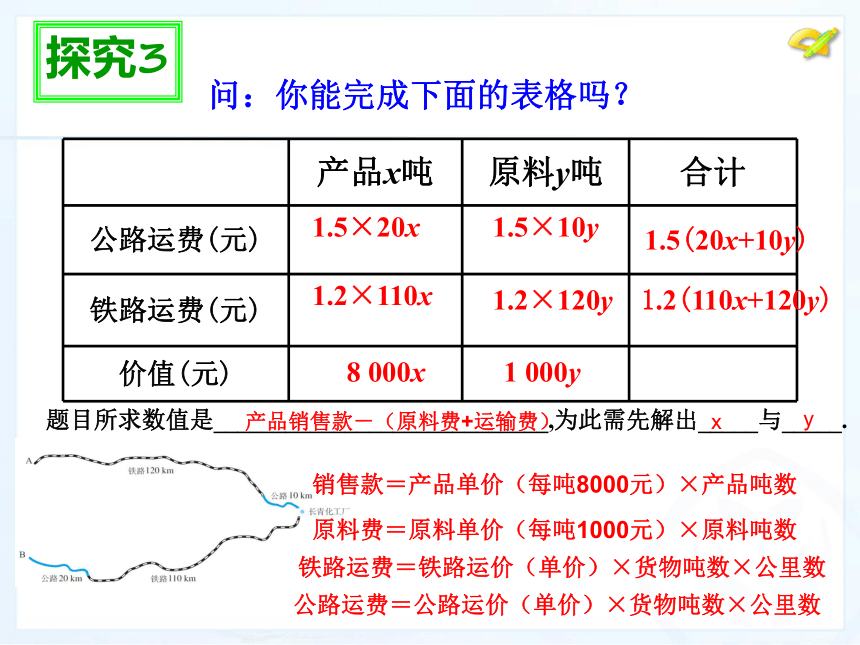
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
探究3
公路运费=公路运价(单价)×货物吨数×公里数
铁路运费=铁路运价(单价)×货物吨数×公里数
原料费=原料单价(每吨1000元)×原料吨数
题目所求数值是____________________________,为此需先解出_____与_____.
问:你能完成下面的表格吗?
1.2×120y
1.2(110x+120y)
8 000x
1 000y
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
产品销售款-(原料费+运输费)
x
y
销售款=产品单价(每吨8000元)×产品吨数
探究3
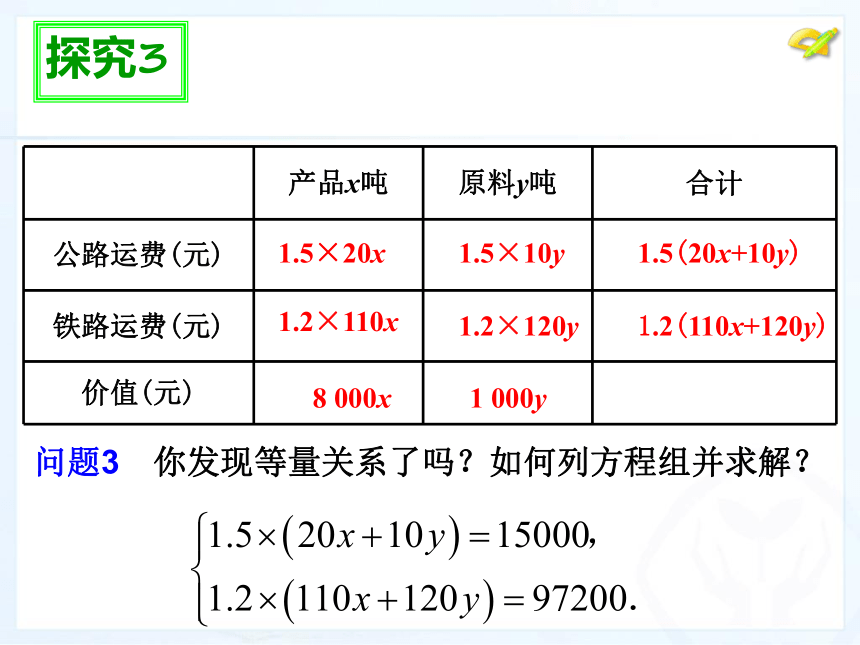
问题3 你发现等量关系了吗?如何列方程组并求解?
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
1.2×120y
1.2(110x+120y)
8 000x
1 000y
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
是原方程组的解.
先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
解:设制成产品x吨,购买原料y吨,由公路、铁路运费可列方程:
探究3
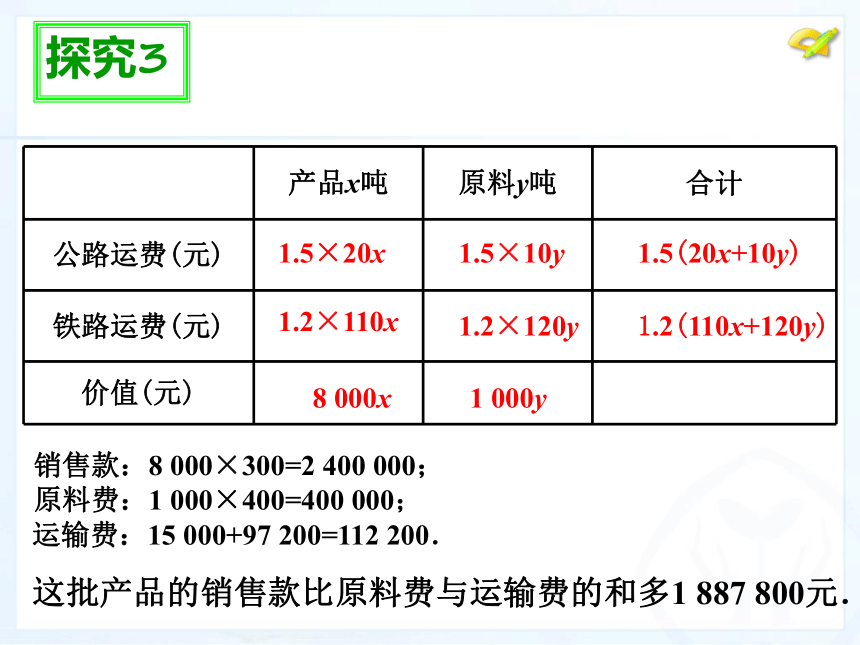
这批产品的销售款比原料费与运输费的和多1 887 800元.
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
1.2×120y
1.2(110x+120y)
8 000x
1 000y
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
销售款:8 000×300=2 400 000;
原料费:1 000×400=400 000;
运输费:15 000+97 200=112 200.
归纳总结
(1)在什么情况下考虑选择设间接未知数?
当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
(2)如何更好地分析“探究3”这样数量关系比较复杂的实际问题?
每种产品的销售总额=售价×销售数量
每种产品的利润总额=单件利润×销售数量
单件利润=售价-成本
行程问题:路程=速度×时间
相遇问题:甲路程+乙路程=总路程
追及问题:(1)同地不同时:前者所用时间-多用时间=追者所用时间
(2)同时不同地:前者路程+两者间的距离=追者路程
行程问题常常用线段表示法分析题目中的数量关系,根据线段长度的内在联系,找出等量关系。
1、(教材101页:习题8.3第2题)A地至B地的航线长9750km,一架飞机从A地顺风飞往B地需12.5h,它逆风飞行同样的航线需13h。求飞机无风时的平均速度与风速。
顺风速度=静风速度+风的速度
逆风速度=静风速度-风的速度
巩固练习
2、(教材P101:习题8.3第3题)一支部队第一天行车4h,第二天行军5h,两天共行军98km,且第一天比第二天少走2km。第一天和第二天行军的平均速度各是多少?
巩固练习
3、(教材102页:习题8.3第4题)用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒。现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
巩固练习
4、(教材102页:习题8.3第6题)从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min。甲地到乙地全路是多少?
路程=速度×时间
注意方程中左右两边单位的统一
巩固练习
巩固练习
5、(教材102页:习题8.3第7题)用含药30%和75%的两种防腐药水,配制含药50%的防腐药水18kg,两种药水各需多少千克?
配制前药质量之和=配制后药的总质量
配制前的药水质量之和=配制后药水总质量
6、(教材P102:习题8.3第9题)某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元。这个记录是否有误?如果有误,请说明理由。
巩固练习
布置作业
全效学习78-79页
(第3课时)
学习目标:
能分析“探究3”中的数量关系,会设间接未知数,列方程组并求解,得到实际问题的答案,体会数学建模思想.
学习重点:
分析复杂问题中的数量关系,建立方程组 .
学习目标与重点
探究3
探究3 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
公路运费=公路运价(单价)×货物吨数×公里数
铁路运费=铁路运价(单价)×货物吨数×公里数
原料费=原料单价(每吨1000元)×原料吨数
销售款=产品单价(每吨8000元)×产品吨数
探究3
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
探究3
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
探究3
公路运费=公路运价(单价)×货物吨数×公里数
铁路运费=铁路运价(单价)×货物吨数×公里数
原料费=原料单价(每吨1000元)×原料吨数
题目所求数值是____________________________,为此需先解出_____与_____.
问:你能完成下面的表格吗?
1.2×120y
1.2(110x+120y)
8 000x
1 000y
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
产品销售款-(原料费+运输费)
x
y
销售款=产品单价(每吨8000元)×产品吨数
探究3
问题3 你发现等量关系了吗?如何列方程组并求解?
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
1.2×120y
1.2(110x+120y)
8 000x
1 000y
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
是原方程组的解.
先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
解:设制成产品x吨,购买原料y吨,由公路、铁路运费可列方程:
探究3
这批产品的销售款比原料费与运输费的和多1 887 800元.
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
1.2×120y
1.2(110x+120y)
8 000x
1 000y
1.5×20x
1.5×10y
1.5(20x+10y)
1.2×110x
销售款:8 000×300=2 400 000;
原料费:1 000×400=400 000;
运输费:15 000+97 200=112 200.
归纳总结
(1)在什么情况下考虑选择设间接未知数?
当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
(2)如何更好地分析“探究3”这样数量关系比较复杂的实际问题?
每种产品的销售总额=售价×销售数量
每种产品的利润总额=单件利润×销售数量
单件利润=售价-成本
行程问题:路程=速度×时间
相遇问题:甲路程+乙路程=总路程
追及问题:(1)同地不同时:前者所用时间-多用时间=追者所用时间
(2)同时不同地:前者路程+两者间的距离=追者路程
行程问题常常用线段表示法分析题目中的数量关系,根据线段长度的内在联系,找出等量关系。
1、(教材101页:习题8.3第2题)A地至B地的航线长9750km,一架飞机从A地顺风飞往B地需12.5h,它逆风飞行同样的航线需13h。求飞机无风时的平均速度与风速。
顺风速度=静风速度+风的速度
逆风速度=静风速度-风的速度
巩固练习
2、(教材P101:习题8.3第3题)一支部队第一天行车4h,第二天行军5h,两天共行军98km,且第一天比第二天少走2km。第一天和第二天行军的平均速度各是多少?
巩固练习
3、(教材102页:习题8.3第4题)用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒。现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
巩固练习
4、(教材102页:习题8.3第6题)从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min。甲地到乙地全路是多少?
路程=速度×时间
注意方程中左右两边单位的统一
巩固练习
巩固练习
5、(教材102页:习题8.3第7题)用含药30%和75%的两种防腐药水,配制含药50%的防腐药水18kg,两种药水各需多少千克?
配制前药质量之和=配制后药的总质量
配制前的药水质量之和=配制后药水总质量
6、(教材P102:习题8.3第9题)某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元。这个记录是否有误?如果有误,请说明理由。
巩固练习
布置作业
全效学习78-79页
