人教版七年级下册数学 9.2一元一次不等式 课件(共20张ppt )
文档属性
| 名称 | 人教版七年级下册数学 9.2一元一次不等式 课件(共20张ppt ) |  | |
| 格式 | pptx | ||
| 文件大小 | 278.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 08:44:02 | ||
图片预览








文档简介
9.2一元一次不等式
我们知道2x+1=5叫做一元一次方程,那么你觉得不等式2x+1>5应该如何命名吗?
想一想
不等式
解
解集
解集的表示方法
一元一次不等式
导航
一元一次不等式
类似于一元一次方程,含有一个未知数且未知数的次数是1的不等式叫做一元一次不等式。
不等式
解
解集
解集的表示方法
一元一次不等式
导航
下列各式是一元一次不等式的是( )
A. 4x-2y≤0
B. x≥-11
C. x2-1≤0
D.
判断一个式子是不是一元一次不等式,必须满足四个条件:
①式中只含有一个未知数;
②未知数的次数是1;
③式子用不等号连接
④分母中不含未知数
注意
尝试练习
不等式
解
解集
解集的表示方法
一元一次不等式
导航
B
思考:有下列数学表达式:
①-1<0;
②3m-2n>0;
③x=4;
④x≠7;
⑤5x+4=x+5;
其中是不等式的有 ( )
是一元一次不等式的有( )(只填序号)
不等式
解
解集
解集的表示方法
一元一次不等式
导航
⑥x2+xy+y2;
⑦x+2>y+3;
⑧x2>4;
⑨3x-2>4x-3;
⑩3+5<7;
①②④⑦⑧⑨⑩
④⑨
圣诞节到了,小明去买贺卡花了x元,买邮票花了3元,他总共花了10元,请问小明买贺卡花了多少元?(列方程求解)
小
明
买
贺
卡
解:由题意,得 x+3=10
移项,得 x =10-3
合并同类项,得 x =7
答:小明买贺卡花了7元.
移项法则的理论依据是
如果小明总共花的钱不足10元呢?根据题意你能列出一个式子吗?
移项要变号。
等式的性质1
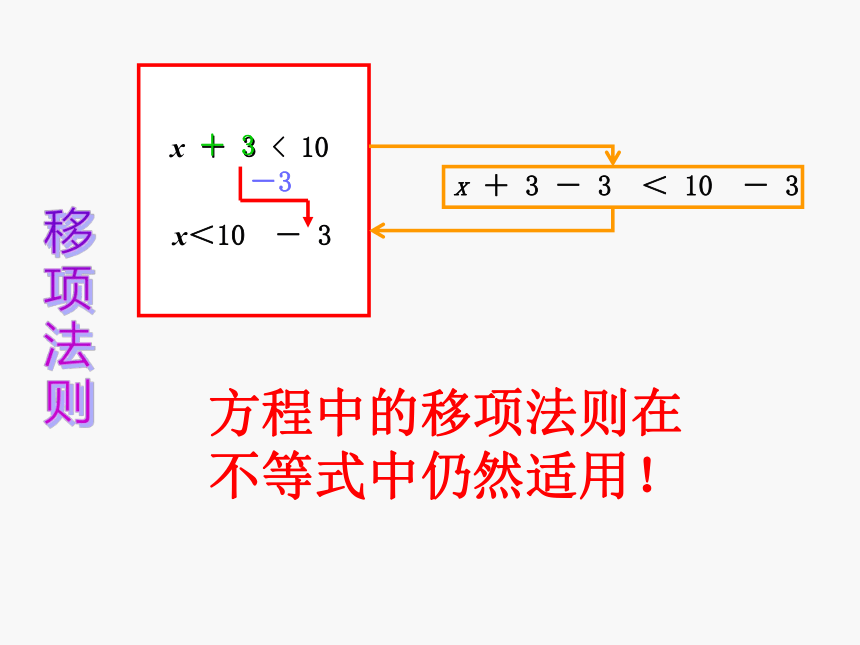
x+3<10
+3
-3
x + 3 < 10
x<10 - 3
+ 3
-3
移
项
法
则
x + 3 - 3 < 10 - 3
方程中的移项法则在不等式中仍然适用!
1
2
3
4
5
6
7
8
-1
-2
-3
-4
解: 移项得 x <10-3
例 1 解一元一次不等式 x + 3 < 10
例
题
讲
解
即 x < 7
这个不等式的解集在数轴上表示如下:
0
问题1:实心小圆点和空心小圆圈分别在什么时候适用
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
例
题
讲
解
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
思考:求满足不等式 8x-2≤7x+3 的正整数解
8x-2≤7x+3
8x-7x≤3+2
x + 3 < 10
x<10 - 3
+ 3
-3
7x
-7x
-2
+2
移
项
法
则
再说一遍:移项要变号,不影响不等号的方向
小
练
习
填 空:
解不等式:1-2x> - 3x + 3
解: 1-2x> - 3x + 3
移项,得 -2x >3
合并,得 >
+3x
-1
x
2
例3 解不等式
3(1-x)>2(1-2x)
例
题
解: 去括号,得 3-3 x >2-4x
移项,得 -3x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是x >-1
比一比,谁做得又快又好!
(1)x+4>3
(2)7x+6 ≥ 6x+3
(3)7x-1 ≤ 6x+1
(4)3-5x < 2(2-3x)
解下列不等式,并把它们的解集在数轴上
表示出来。
练
习
例
解不等式3+3x>2+4x
解:移项,得 -4x+3x>2- 3
合并同类项,得 -x>-1
∴ 原不等式的解集是 x<1
写不等式的解集时,要把表示未知数的字母写在不等号的左边。
例如
1、求不等式
3(x-3)+6 < 2x+1的正整数解。
思考
2、X取什么值时,代数式x+ 的值。
(1)大于0 (2)不小于-
想
一
想
例: 三角形中任意两边之差
与第三边有怎样的大小关系?
想一想
a
c
b
三角形中任意两边之差小于第三边
从中你得到什么规律?
解:如图,设a,b,c为任意一个三角
形的三条边的长,则
a+b>c, b+c>a, c+a>b.
由式子a+b>c 移项可得
a>c-b, b>c-a .
类似地,由式子b+c>a及c+a>b移项可得
c>a-b, b>a-c 及 c>b-a, a>b-c
求满足不等式
2(1-2X)-5+X<1-2X的负整数解
m为何值时,方程 的解是非正数.
例:某次“人与自然”的知识竟赛中共有20道题。对于每一道题,答对了得10分,答错了或不答扣5分,至少要答对几道题,其得分不少于80分?
解:设答对的题数是x,则答对或不答的题数为20-x,根据题意,得
10x – 5(20 – x) ≥ 80
解这个不等式,得: x ≥ 12
答:……
1、不等式性质1:不等式的两边__加上或__减去__一个数或式,所得到的不等式____.
小
结
都
都
同
仍成立
2、不等式移项法则:把不等式的任何一项的_____后,从_______的___移到_______,所得到的不等式仍成立。
符号改变
一边
另一边
不等号
问题
某地庆典活动需燃放某种礼花弹,为确
保人身安全,要求燃放者在点燃导火索后于
燃放前转移到10米以外的地方.已知导火
索的燃烧速度为0.02米(每秒),人离开的
速度是4米(每秒),导火索的长x米应满足
怎样的关系?
你会运用已学知识解这个不等式吗?
我们知道2x+1=5叫做一元一次方程,那么你觉得不等式2x+1>5应该如何命名吗?
想一想
不等式
解
解集
解集的表示方法
一元一次不等式
导航
一元一次不等式
类似于一元一次方程,含有一个未知数且未知数的次数是1的不等式叫做一元一次不等式。
不等式
解
解集
解集的表示方法
一元一次不等式
导航
下列各式是一元一次不等式的是( )
A. 4x-2y≤0
B. x≥-11
C. x2-1≤0
D.
判断一个式子是不是一元一次不等式,必须满足四个条件:
①式中只含有一个未知数;
②未知数的次数是1;
③式子用不等号连接
④分母中不含未知数
注意
尝试练习
不等式
解
解集
解集的表示方法
一元一次不等式
导航
B
思考:有下列数学表达式:
①-1<0;
②3m-2n>0;
③x=4;
④x≠7;
⑤5x+4=x+5;
其中是不等式的有 ( )
是一元一次不等式的有( )(只填序号)
不等式
解
解集
解集的表示方法
一元一次不等式
导航
⑥x2+xy+y2;
⑦x+2>y+3;
⑧x2>4;
⑨3x-2>4x-3;
⑩3+5<7;
①②④⑦⑧⑨⑩
④⑨
圣诞节到了,小明去买贺卡花了x元,买邮票花了3元,他总共花了10元,请问小明买贺卡花了多少元?(列方程求解)
小
明
买
贺
卡
解:由题意,得 x+3=10
移项,得 x =10-3
合并同类项,得 x =7
答:小明买贺卡花了7元.
移项法则的理论依据是
如果小明总共花的钱不足10元呢?根据题意你能列出一个式子吗?
移项要变号。
等式的性质1
x+3<10
+3
-3
x + 3 < 10
x<10 - 3
+ 3
-3
移
项
法
则
x + 3 - 3 < 10 - 3
方程中的移项法则在不等式中仍然适用!
1
2
3
4
5
6
7
8
-1
-2
-3
-4
解: 移项得 x <10-3
例 1 解一元一次不等式 x + 3 < 10
例
题
讲
解
即 x < 7
这个不等式的解集在数轴上表示如下:
0
问题1:实心小圆点和空心小圆圈分别在什么时候适用
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
例
题
讲
解
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
思考:求满足不等式 8x-2≤7x+3 的正整数解
8x-2≤7x+3
8x-7x≤3+2
x + 3 < 10
x<10 - 3
+ 3
-3
7x
-7x
-2
+2
移
项
法
则
再说一遍:移项要变号,不影响不等号的方向
小
练
习
填 空:
解不等式:1-2x> - 3x + 3
解: 1-2x> - 3x + 3
移项,得 -2x >3
合并,得 >
+3x
-1
x
2
例3 解不等式
3(1-x)>2(1-2x)
例
题
解: 去括号,得 3-3 x >2-4x
移项,得 -3x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是x >-1
比一比,谁做得又快又好!
(1)x+4>3
(2)7x+6 ≥ 6x+3
(3)7x-1 ≤ 6x+1
(4)3-5x < 2(2-3x)
解下列不等式,并把它们的解集在数轴上
表示出来。
练
习
例
解不等式3+3x>2+4x
解:移项,得 -4x+3x>2- 3
合并同类项,得 -x>-1
∴ 原不等式的解集是 x<1
写不等式的解集时,要把表示未知数的字母写在不等号的左边。
例如
1、求不等式
3(x-3)+6 < 2x+1的正整数解。
思考
2、X取什么值时,代数式x+ 的值。
(1)大于0 (2)不小于-
想
一
想
例: 三角形中任意两边之差
与第三边有怎样的大小关系?
想一想
a
c
b
三角形中任意两边之差小于第三边
从中你得到什么规律?
解:如图,设a,b,c为任意一个三角
形的三条边的长,则
a+b>c, b+c>a, c+a>b.
由式子a+b>c 移项可得
a>c-b, b>c-a .
类似地,由式子b+c>a及c+a>b移项可得
c>a-b, b>a-c 及 c>b-a, a>b-c
求满足不等式
2(1-2X)-5+X<1-2X的负整数解
m为何值时,方程 的解是非正数.
例:某次“人与自然”的知识竟赛中共有20道题。对于每一道题,答对了得10分,答错了或不答扣5分,至少要答对几道题,其得分不少于80分?
解:设答对的题数是x,则答对或不答的题数为20-x,根据题意,得
10x – 5(20 – x) ≥ 80
解这个不等式,得: x ≥ 12
答:……
1、不等式性质1:不等式的两边__加上或__减去__一个数或式,所得到的不等式____.
小
结
都
都
同
仍成立
2、不等式移项法则:把不等式的任何一项的_____后,从_______的___移到_______,所得到的不等式仍成立。
符号改变
一边
另一边
不等号
问题
某地庆典活动需燃放某种礼花弹,为确
保人身安全,要求燃放者在点燃导火索后于
燃放前转移到10米以外的地方.已知导火
索的燃烧速度为0.02米(每秒),人离开的
速度是4米(每秒),导火索的长x米应满足
怎样的关系?
你会运用已学知识解这个不等式吗?
