人教版数学七年级下册 7.2.2《用坐标表示平移》 课件(共31张PPT)
文档属性
| 名称 | 人教版数学七年级下册 7.2.2《用坐标表示平移》 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览








文档简介
让心灵去旅行 ...
人生就象一场旅行
不必在乎目的地
在乎的是沿途的风景
以及,看风景的心情
体 验 回 顾
1. 什么叫做平移?
2 .平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形只改变位置,形状、大小不变。
3.连结各组对应点的线段
平行且相等。
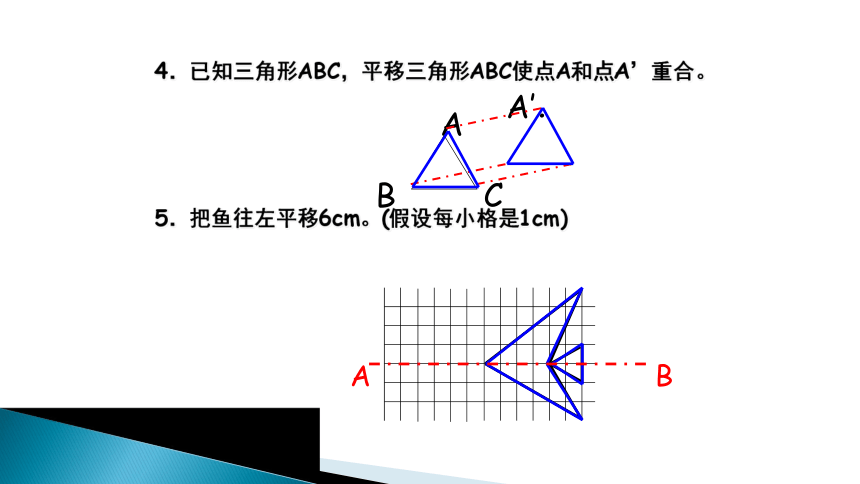
4.已知三角形ABC,平移三角形ABC使点A和点A’重合。
5.把鱼往左平移6cm。(假设每小格是1cm)
A
B
B
A
C
A’.
-3
-2
-1
0
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
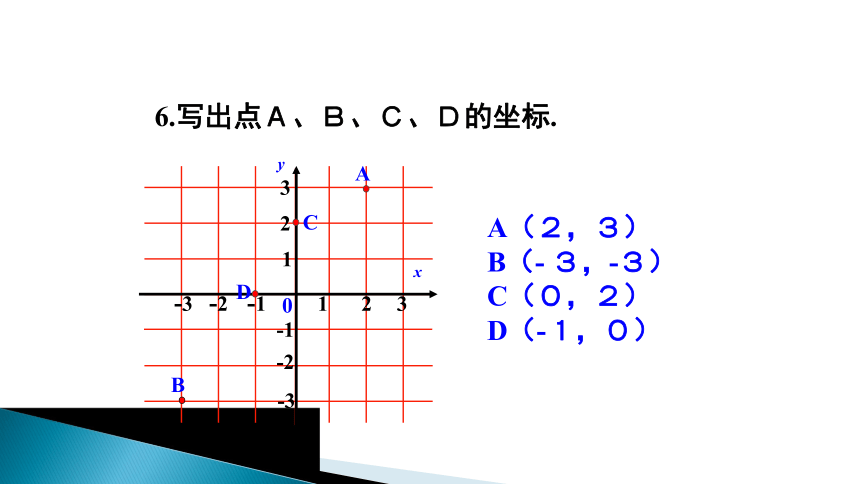
6.写出点A、B、C、D的坐标.
A(2,3) B(- 3,-3) C(0,2)
D(-1,0)
7.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
(+ , +)
(- , +)
(- , -)
(+ , -)
(0 , y)
(x, 0)
每个象限内的点都有自已的符号特征.
用坐标表示平移
1
2
3
学习目标
掌握坐标变化与图形平移的关系,能利用点的平移规律将平面图形进行平移;
会根据图形上点的坐标的变化,来判定图形的移动过程;
发展学生的形象思维能力和数形结合的意识。
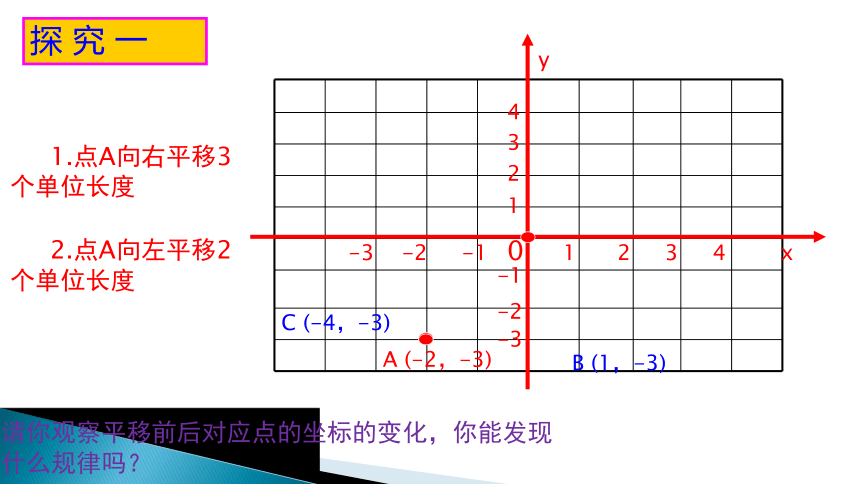
探 究 一
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-3)
y
1.点A向右平移3个单位长度
2.点A向左平移2个单位长度
B (1,-3)
请你观察平移前后对应点的坐标的变化,你能发现什么规律吗?
C (-4,-3)
探 究 二
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-1)
y
C (-2,-3)
B (-2,2)
1.点A向上平移3个单位长度
2.点A向下平移2个单位长度
请你观察对应点的坐标的变化,你能发现什么规律吗?
^
y
>
x
0
1
1
2
3
4
3
-1
-3
-1
-2
-3
-4
?
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标.30秒后,飞机P飞到P′位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗?
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
总结规律1:
图形平移与点的坐标变化间的关系(a>0,b>0)
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标
(4,3),B(3,1),C(1,2)
(1)将三角形ABC三
个顶点的横坐标都减去6,
纵坐标不变,分别得到
点A1,B1,C1
(2)依次连接A1,B1,C1,
各点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的 大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 .
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 0 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
将△ABC三个顶点的纵坐标都减去5,横坐标不变.分别得到点A2,B2,C2
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和位置上有什么关系?
2.例题探索
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系(a>0,b>0)
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2:
合作交流
1.游戏巩固(点的平移,坐标的变换)
小组任务:
(1)寻找路线,并用坐标表示
(2)独立思考,形成主见
(3)讨论交流
合作交流
2:游戏巩固(图形的平移,坐标的变换)
如图,与(1)的三角形相比,请抢答:(2)(3)中的三角形发生了哪些变化? 图中直角三角形顶点的坐标分别发生了什么变化?
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(2)
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(2)
0
(1)
⑴如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A'B'C'D',画出平移后的图形,并指出其各个顶点的坐标.
图形的平移和点的坐标变化
练一练:
A′
B′
C′
D′
解:如图所示,四边形A′B′C′D′就是所 要画的四边形.
A′(-3,1), B′(1,1), C′(2,4), D′(-2,4)
图形的平移和点的坐标变化
⑵已知点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5 个单位长度,得到G′,则G′的坐标为( )
练一练:
A.(6,5) B.(4,5)
C.(6,3) D.(4,3)
D
你做对了吗?
五、强化训练
1、已知点A、B的坐标分别为A(-3,2)
B(1,2),则点A向右平移___个单位长度可得到点B.
2、已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,-2) 的位置上,则点B,C的坐标分别为__________,__________.
3、正方形的四个顶点中,A(-1,2), B(3,2),
C(3,-2),则第四个顶点D 的坐标为______.
4
(5,-3)
(3,-6)
(-1,-2)
向左平移
a个单位
向下平移
个单位
b
向上平移
个单位
b
向右平移
a个单位
小结
P(x, y)
P(x, y-b)
P(x, y+b)
P(x-a, y)
P(x+a, y)
拓展训练
A组题
1. 在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是 。
2. 线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为______________。
3.如图 (1) ,将平行四边形ABCD向左平移 2个单位长度,可以得到A’B’C’D’,画出平移后的图形,并指出其各个顶点的坐标。
拓展训练
B组题
1. 有相距5个单位的两点A(- 3,a),B(b,4),AB//x轴,则 a= ,b= 。
2. 三角形DEF是由三角形ABC平移得到的,点A(-1,-4)的对应点为D(1,-1),则点B(1,1)的对应点E、点C(-1,4)的对应点F的坐标分别为( )
A、(2,2),(3,4) B、(3,4),(1,7)
C、(-2,2),(1,7) D、(3,4),(2,-2)
3. 如图(2),三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移到三角形A1B1C1。求A1、B1、C1的坐标。
拓展训练
C组题
如图所示的鱼是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)作如下变化:
①纵坐标保持不变,横坐标分别变成原来的2倍;
②横坐标保持不变,纵坐标分别变成原来的2倍;
③纵坐标、横坐标分别变成原来的2倍;
再将所得的点用线段依次连接起来,所得图案与原来图案相比有什么变化?
1. 将P(- 4,3)沿x轴负方向平移两个单位长度,再沿y轴负方向平移两个单位长度,所得到的点的坐标为 。
2. 将点A(4,3)向 平移 个单位长度后,其坐标的变化是?
3. 已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 。
4. 将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=___________ 。
5. 已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A、(-2,2),(3,4),(1,7)
B、(-2,2),(4,3),(1,7)
C、(2,2),(3,4),(1,7)
D、(2,-2),(3,3),(1,7)
6. 线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为______________。
回顾自测
作业:
1、将四边形ABCD的四个顶点的横坐标都减去6,同时纵坐标都减去5,得到的结论是( ).
A.先向左平移6个单位,再向下平移5个单位.
B.先向右平移6各单位,再向下平移5各单位.
C.先向左平移6各单位,再向上平移5各单位.
D.先向右平移6个单位,再向上平移5各单位.
A
y
O
1
2
3
4
5
6
7
-1
-2
1
2
3
4
5
6
7
8
x
2、将图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(4,-2)作如下变化
(1)纵坐标不变,横坐标分别加3,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比,有什么变化.
(2)横坐标保持不变,纵坐标分别加3,所得图案与原图案相比,有什么变化.
探索
3、如果将图中的横坐标都乘以2 能得到什么结论?画出图形.
3
1
4
2
5
-2
-4
-1
-3
2
3
4
5
6
7
-2
-1
O
1
x
y
A
B
C
y
x
3
2
4
5
2
4
(2,4)
4、如图所示,在直角坐标系下,图1中的图案“A”经过变换分别变成图2~图6中的相应图案(虚线对应于原图案),试写出图2~图6中各顶点的坐标,探索每次变换前后图案发生了什么变化、对应点的坐标之间有什么关系.
y
x
3
2
4
5
2
4
(2,4)
6
7
8
(4,4)
图一
图二
y
x
3
2
4
5
2
4
(2,4)
6
7
(5,4)
y
x
3
2
4
5
2
4
(2,4)
6
7
(2,-4)
图三
图四
y
x
3
2
4
5
2
4
(2,4)
6
(2,8)
8
y
x
3
2
4
2
4
(2,4)
(4,8)
8
8
图五
图六
人生就象一场旅行
不必在乎目的地
在乎的是沿途的风景
以及,看风景的心情
体 验 回 顾
1. 什么叫做平移?
2 .平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形只改变位置,形状、大小不变。
3.连结各组对应点的线段
平行且相等。
4.已知三角形ABC,平移三角形ABC使点A和点A’重合。
5.把鱼往左平移6cm。(假设每小格是1cm)
A
B
B
A
C
A’.
-3
-2
-1
0
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
6.写出点A、B、C、D的坐标.
A(2,3) B(- 3,-3) C(0,2)
D(-1,0)
7.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
(+ , +)
(- , +)
(- , -)
(+ , -)
(0 , y)
(x, 0)
每个象限内的点都有自已的符号特征.
用坐标表示平移
1
2
3
学习目标
掌握坐标变化与图形平移的关系,能利用点的平移规律将平面图形进行平移;
会根据图形上点的坐标的变化,来判定图形的移动过程;
发展学生的形象思维能力和数形结合的意识。
探 究 一
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-3)
y
1.点A向右平移3个单位长度
2.点A向左平移2个单位长度
B (1,-3)
请你观察平移前后对应点的坐标的变化,你能发现什么规律吗?
C (-4,-3)
探 究 二
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-1)
y
C (-2,-3)
B (-2,2)
1.点A向上平移3个单位长度
2.点A向下平移2个单位长度
请你观察对应点的坐标的变化,你能发现什么规律吗?
^
y
>
x
0
1
1
2
3
4
3
-1
-3
-1
-2
-3
-4
?
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标.30秒后,飞机P飞到P′位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗?
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
总结规律1:
图形平移与点的坐标变化间的关系(a>0,b>0)
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标
(4,3),B(3,1),C(1,2)
(1)将三角形ABC三
个顶点的横坐标都减去6,
纵坐标不变,分别得到
点A1,B1,C1
(2)依次连接A1,B1,C1,
各点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的 大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 .
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 0 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
将△ABC三个顶点的纵坐标都减去5,横坐标不变.分别得到点A2,B2,C2
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和位置上有什么关系?
2.例题探索
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系(a>0,b>0)
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2:
合作交流
1.游戏巩固(点的平移,坐标的变换)
小组任务:
(1)寻找路线,并用坐标表示
(2)独立思考,形成主见
(3)讨论交流
合作交流
2:游戏巩固(图形的平移,坐标的变换)
如图,与(1)的三角形相比,请抢答:(2)(3)中的三角形发生了哪些变化? 图中直角三角形顶点的坐标分别发生了什么变化?
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(2)
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(2)
0
(1)
⑴如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A'B'C'D',画出平移后的图形,并指出其各个顶点的坐标.
图形的平移和点的坐标变化
练一练:
A′
B′
C′
D′
解:如图所示,四边形A′B′C′D′就是所 要画的四边形.
A′(-3,1), B′(1,1), C′(2,4), D′(-2,4)
图形的平移和点的坐标变化
⑵已知点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5 个单位长度,得到G′,则G′的坐标为( )
练一练:
A.(6,5) B.(4,5)
C.(6,3) D.(4,3)
D
你做对了吗?
五、强化训练
1、已知点A、B的坐标分别为A(-3,2)
B(1,2),则点A向右平移___个单位长度可得到点B.
2、已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,-2) 的位置上,则点B,C的坐标分别为__________,__________.
3、正方形的四个顶点中,A(-1,2), B(3,2),
C(3,-2),则第四个顶点D 的坐标为______.
4
(5,-3)
(3,-6)
(-1,-2)
向左平移
a个单位
向下平移
个单位
b
向上平移
个单位
b
向右平移
a个单位
小结
P(x, y)
P(x, y-b)
P(x, y+b)
P(x-a, y)
P(x+a, y)
拓展训练
A组题
1. 在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是 。
2. 线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为______________。
3.如图 (1) ,将平行四边形ABCD向左平移 2个单位长度,可以得到A’B’C’D’,画出平移后的图形,并指出其各个顶点的坐标。
拓展训练
B组题
1. 有相距5个单位的两点A(- 3,a),B(b,4),AB//x轴,则 a= ,b= 。
2. 三角形DEF是由三角形ABC平移得到的,点A(-1,-4)的对应点为D(1,-1),则点B(1,1)的对应点E、点C(-1,4)的对应点F的坐标分别为( )
A、(2,2),(3,4) B、(3,4),(1,7)
C、(-2,2),(1,7) D、(3,4),(2,-2)
3. 如图(2),三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移到三角形A1B1C1。求A1、B1、C1的坐标。
拓展训练
C组题
如图所示的鱼是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)作如下变化:
①纵坐标保持不变,横坐标分别变成原来的2倍;
②横坐标保持不变,纵坐标分别变成原来的2倍;
③纵坐标、横坐标分别变成原来的2倍;
再将所得的点用线段依次连接起来,所得图案与原来图案相比有什么变化?
1. 将P(- 4,3)沿x轴负方向平移两个单位长度,再沿y轴负方向平移两个单位长度,所得到的点的坐标为 。
2. 将点A(4,3)向 平移 个单位长度后,其坐标的变化是?
3. 已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 。
4. 将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=___________ 。
5. 已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A、(-2,2),(3,4),(1,7)
B、(-2,2),(4,3),(1,7)
C、(2,2),(3,4),(1,7)
D、(2,-2),(3,3),(1,7)
6. 线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为______________。
回顾自测
作业:
1、将四边形ABCD的四个顶点的横坐标都减去6,同时纵坐标都减去5,得到的结论是( ).
A.先向左平移6个单位,再向下平移5个单位.
B.先向右平移6各单位,再向下平移5各单位.
C.先向左平移6各单位,再向上平移5各单位.
D.先向右平移6个单位,再向上平移5各单位.
A
y
O
1
2
3
4
5
6
7
-1
-2
1
2
3
4
5
6
7
8
x
2、将图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(4,-2)作如下变化
(1)纵坐标不变,横坐标分别加3,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比,有什么变化.
(2)横坐标保持不变,纵坐标分别加3,所得图案与原图案相比,有什么变化.
探索
3、如果将图中的横坐标都乘以2 能得到什么结论?画出图形.
3
1
4
2
5
-2
-4
-1
-3
2
3
4
5
6
7
-2
-1
O
1
x
y
A
B
C
y
x
3
2
4
5
2
4
(2,4)
4、如图所示,在直角坐标系下,图1中的图案“A”经过变换分别变成图2~图6中的相应图案(虚线对应于原图案),试写出图2~图6中各顶点的坐标,探索每次变换前后图案发生了什么变化、对应点的坐标之间有什么关系.
y
x
3
2
4
5
2
4
(2,4)
6
7
8
(4,4)
图一
图二
y
x
3
2
4
5
2
4
(2,4)
6
7
(5,4)
y
x
3
2
4
5
2
4
(2,4)
6
7
(2,-4)
图三
图四
y
x
3
2
4
5
2
4
(2,4)
6
(2,8)
8
y
x
3
2
4
2
4
(2,4)
(4,8)
8
8
图五
图六
