人教版数学七年级下册 8.2--消元解二元一次方程组-代入法 (第一课时 共23张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.2--消元解二元一次方程组-代入法 (第一课时 共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 08:50:33 | ||
图片预览


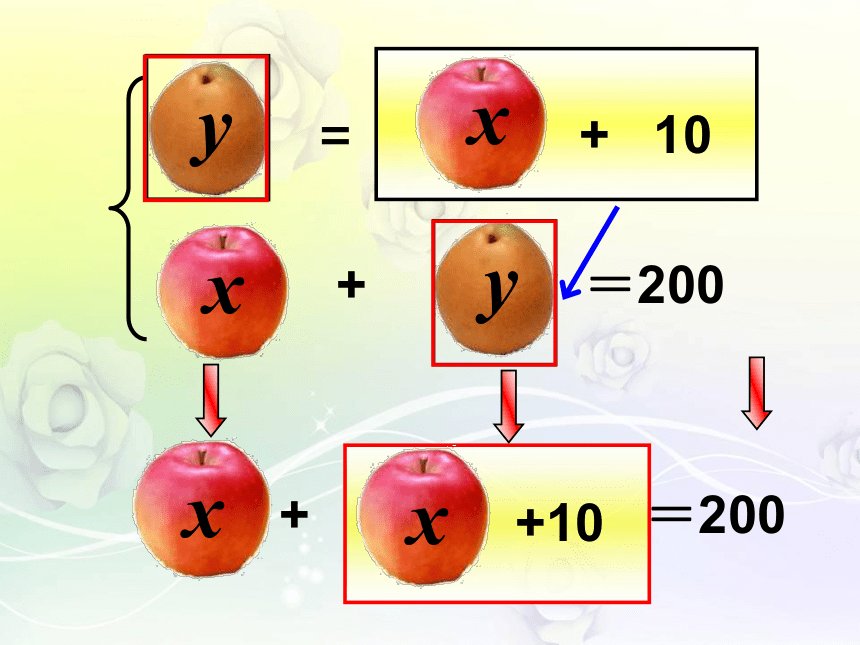


文档简介
第八章 二元一次方程组
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿
8.2 消元—解二元一次方程组
第1课时 代入法
学习目标
1.掌握代入消元法的意义;
2.会用代入法解二元一次方程组;(重点、难点)
讲授新课
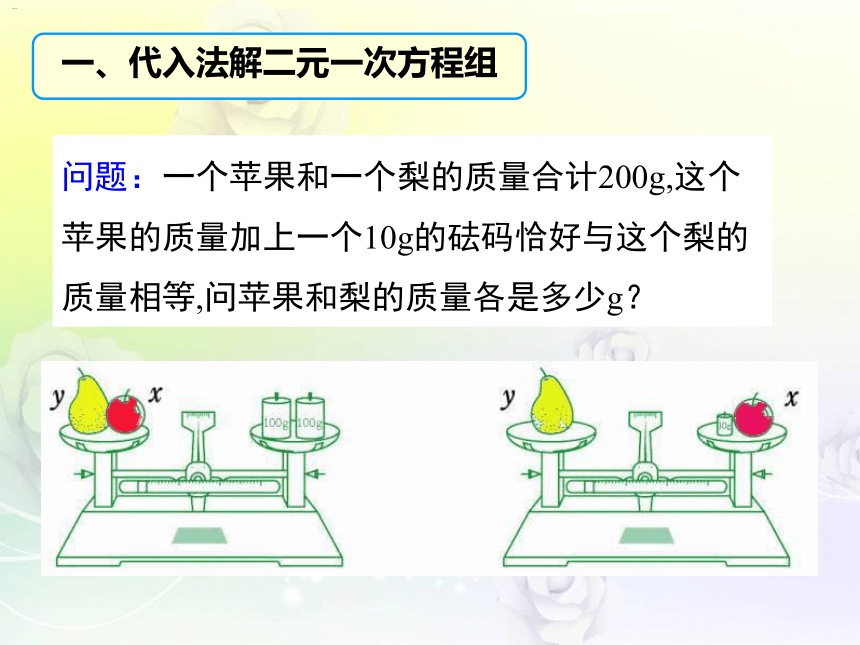
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
一、代入法解二元一次方程组
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
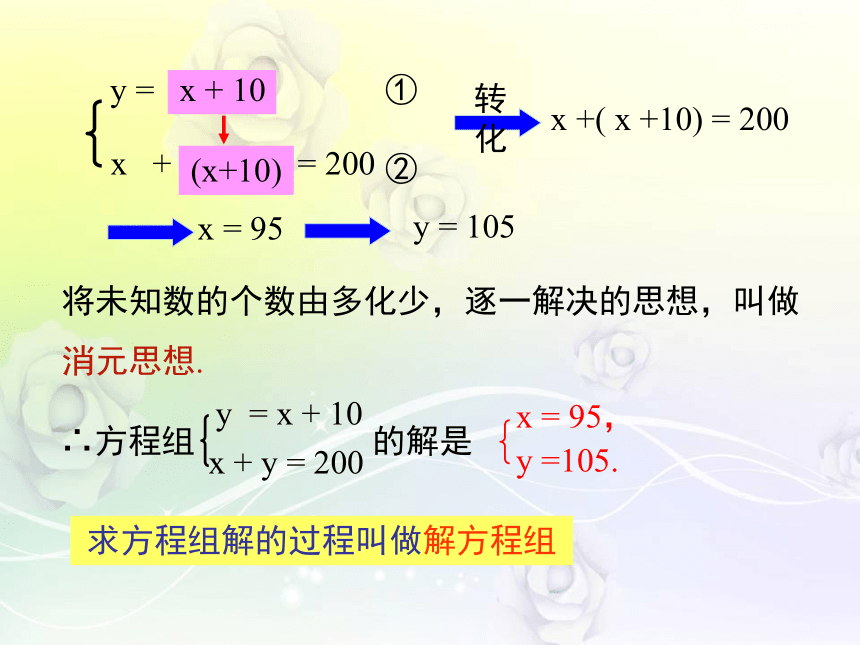
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
主要步骤是:将含一个未知数表示另一个未知数的代数式,代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法。
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
分析
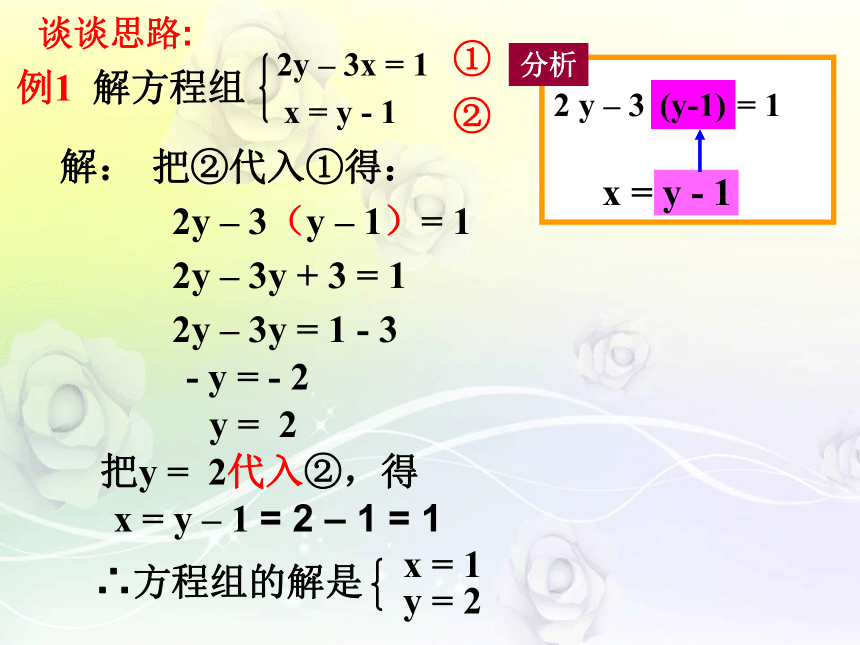
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路:
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变:
2y – 3x = 1
x – y = – 1
①
②
谈谈思路:
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
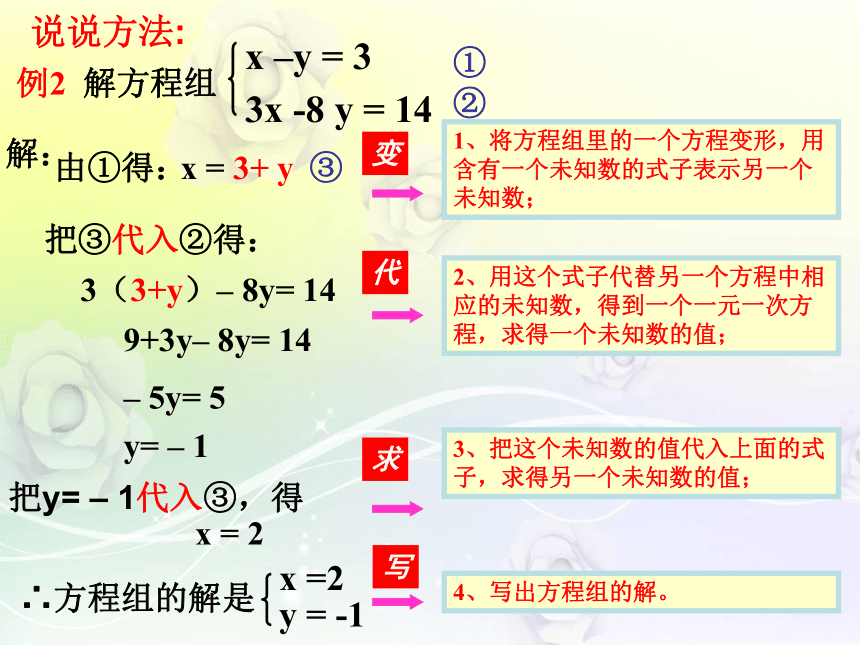
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法:
当堂练习
y=2x,
x+y=12;
(1)
(2)
2x=y-5,
4x+3y=65.
解:
(1)
x=4
y=8
(2)
1.用代入消元法解下列方程组.
x=5
y=15
2、把下列方程分别用含x的式子表示y,含y的式子表示x:
(1)2x-y=3 (2)3x+2y=1
例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
⑴大瓶数
小瓶数
⑵大瓶所装消毒液
小瓶所装消毒液
总生产量.
二、代入法解二元一次方程组的简单应用
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
③
①
由 得:
把 代入 得:
③
②
解得:x=20000
把x=20000代入 得:y=50000
③
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
?
í
ì
=
+
=
22500000
250
500
2
5
y
x
y
x
李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?
解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
二元一次方程组
消去
一元一次方程
变形
代入
解得
解得
用
代替
,消去未知数
50 000
y
=
再议代入消元法
总结归纳
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
2 . 已知 是二元一次方程组
的解,则 a= ,b= 。
3.已知 (a+2b-5)2+|4a+b-6|=0,
求a和b的值.
3
1
bx+ay = 5
ax+by = 7
a=1
b=2
4、如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( )
A
B
C
D
C
5、已知钢笔每只5元,圆珠笔每只2元,小明用16元钱买了这两种笔共5支,试求小明买钢笔和圆珠笔各多少支?
解:设小明买钢笔x支,买圆珠笔y支,根据题意列出方程组得
x+y=5
5x+2y=16
解得:
x=2
y=3
答:小明买钢笔2支,买圆珠笔3支.
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
课堂小结
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿
8.2 消元—解二元一次方程组
第1课时 代入法
学习目标
1.掌握代入消元法的意义;
2.会用代入法解二元一次方程组;(重点、难点)
讲授新课
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
一、代入法解二元一次方程组
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
主要步骤是:将含一个未知数表示另一个未知数的代数式,代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法。
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
分析
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路:
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变:
2y – 3x = 1
x – y = – 1
①
②
谈谈思路:
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法:
当堂练习
y=2x,
x+y=12;
(1)
(2)
2x=y-5,
4x+3y=65.
解:
(1)
x=4
y=8
(2)
1.用代入消元法解下列方程组.
x=5
y=15
2、把下列方程分别用含x的式子表示y,含y的式子表示x:
(1)2x-y=3 (2)3x+2y=1
例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
⑴大瓶数
小瓶数
⑵大瓶所装消毒液
小瓶所装消毒液
总生产量.
二、代入法解二元一次方程组的简单应用
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
③
①
由 得:
把 代入 得:
③
②
解得:x=20000
把x=20000代入 得:y=50000
③
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
?
í
ì
=
+
=
22500000
250
500
2
5
y
x
y
x
李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?
解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
二元一次方程组
消去
一元一次方程
变形
代入
解得
解得
用
代替
,消去未知数
50 000
y
=
再议代入消元法
总结归纳
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
2 . 已知 是二元一次方程组
的解,则 a= ,b= 。
3.已知 (a+2b-5)2+|4a+b-6|=0,
求a和b的值.
3
1
bx+ay = 5
ax+by = 7
a=1
b=2
4、如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( )
A
B
C
D
C
5、已知钢笔每只5元,圆珠笔每只2元,小明用16元钱买了这两种笔共5支,试求小明买钢笔和圆珠笔各多少支?
解:设小明买钢笔x支,买圆珠笔y支,根据题意列出方程组得
x+y=5
5x+2y=16
解得:
x=2
y=3
答:小明买钢笔2支,买圆珠笔3支.
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
课堂小结
