人教版数学七年级下册 第九章不等式与不等式组 复习课 课件 (共19张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第九章不等式与不等式组 复习课 课件 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 553.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览






文档简介
复习课
七年级数学第九章
学习目标:
1.检查学生对本章知识掌握情况;
2.训练学生自主梳理能力,运用和综合分析能力。
3.带领学生查漏补缺。
回顾
1.不等式的基本性质有哪些?
2.解一元一次不等式与解一元一次方程,有哪些相同之处与不同之处?
3.应用一元一次不等式解决实际问题的一般步骤是什么?
4.如何确定一元一次不等式组的解集?
不等式:一般地,用符号“<”“>”“≤ ”“≥”表示大小关系的式子叫做不等式。 不等式的解:使不等式成立的未知数的值,叫做不等式的解。
不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。
一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
一元一次不等式组的解集:一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。 三、定理与性质 不等式的性质:
不等式的基本性质1:不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变。 不等式的基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。 不等式的基本性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
知识点
A
√
√
×
√
√
×
√
一元一次不等式的定义和性质
考点1
下列式子中,一元一次不等式有( )
①3x-1≥4
② 2+3x>6
③ 3- <5
④
⑤
⑥ x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
例1
【归纳拓展】一元一次不等式的概念含几个要点:
(1)用不等号连接;
(2)不等号两边都是关于未知数的整式;
(3)只含有一个未知数,且含有未知数的项的最高
次数为1.
【迁移应用1】
如果aA.
B.
C.
D.
B
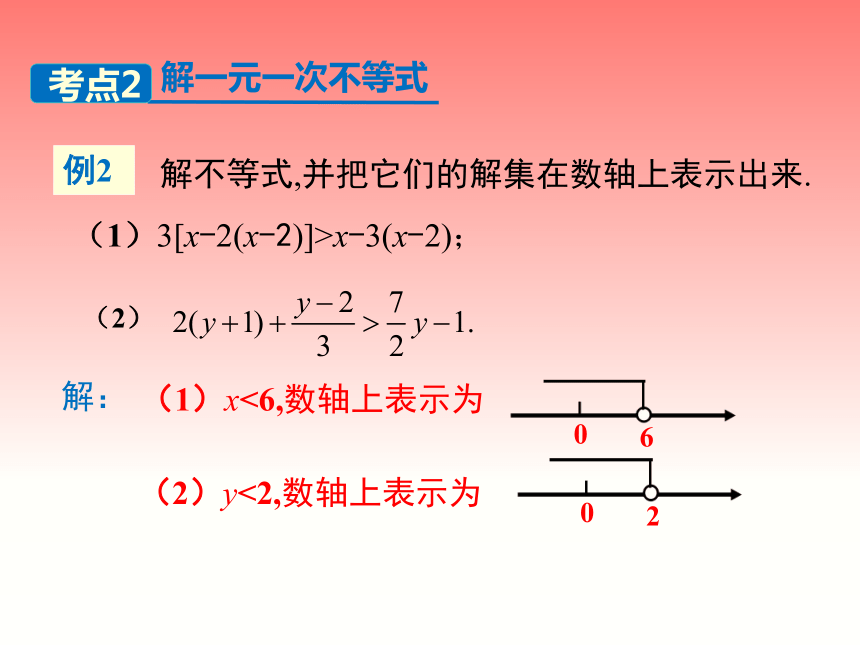
解不等式,并把它们的解集在数轴上表示出来.
(1)3[x-2(x-2)]>x-3(x-2);
(2)
解:
(1)x<6,数轴上表示为
0
6
(2)y<2,数轴上表示为
0
2
解一元一次不等式
考点2
例2
【归纳拓展】解不等式一定要把握好基础知识:
①不等式的性质;②去分母,去括号,合并同类项.
熟练掌握并利用这些基础知识解题,保证准确率.
【迁移应用2】
不等式4x-6 ≥7x-12的非负整数解为 .
0,1,2
小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
分析:从路程下手找不等关系:
即小亮40分钟行进路程≥小明从8时20分到11时行进路程.
解:设小亮的速度为x千米/时,40分= 小时,
列不等式,得 ,解得x≥16.
小亮的速度至少为16千米/时.
例3
一元一次不等式的应用
考点3
【迁移应用3】
当x ___ 时,代数式 的值不小于 的值,此时x的最小整数值是 .
【归纳拓展】不等式的应用情况很多,但解所有的题目关键在于找准表示不等关系的语句,并能够列出不等式,再利用不等式的性质解不等式,这样问题才能得以解决.
≥-0.75
0
已知不等式组 有解,则a的取值范围为
( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
解析:解不等式x-a≥0,得x≥a;解不等式-2x>-4,得x<2.因为不等式组有解,故2在a的右边,即a<2.
一元一次不等式组的定义与解集
考点4
例4
【归纳拓展】不等式组的解集确定方法除利用数轴直观确定外,还可以用口诀确定:同大取大,同小取小,大小小大中间找,大大小小没得找.
【迁移应用4】
下列说法中,正确的个数是( )
①x=7是不等式组 的解;②不等式组 的解集是
-2≤x<3; ③不等式组 的解集是x=6; ④关于x的不等式组
无解.
x>1
x>-1
x>3
x≥-2
x≥6
x≤6
x>4
x<2
A.1个 B.2个 C.3个 D.4个
C
解不等式组:
①
②
解:①不等式组的解集是 ;
②不等式组的解集是x≥9.
例5
解一元一次不等式组
考点5
【归纳拓展】解不等式组的基础是解不等式,把每个不等式的解集解出来后,按求不等式组解集的口诀或利用画数轴的方法找到解集.
【迁移应用5】
不等式组 的所有整数解的和是 .
2x-1>1,
-4x≥-2x-8
提示:不等式组的解集是19
一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5所以x=6,7,8.
小朋友有6人,玩具有22件;或小朋友有7人,玩具有25件;或小朋友有8人,玩具有28件.
用一元一次不等式组解决实际问题
考点6
例6
【归纳拓展】当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属于通过列不等式(组)来解决的问题,而不属于通过列方程(组)来解决的问题.
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
课后训练
1.已知点M(3a-9,1-a)在第三象限,且它的横、纵坐标都
是整数,则a的值是( )
A. 1 B. 2 C. 3 D. 0
2.关于x的不等式x-2a≤1的解集如图所示,则a的值是 .
-1
0
1
B
-1
4.解不等式组: ,并把解集在数轴上表
示出来.
3.解不等式
解:x ≤8
解:1
七年级数学第九章
学习目标:
1.检查学生对本章知识掌握情况;
2.训练学生自主梳理能力,运用和综合分析能力。
3.带领学生查漏补缺。
回顾
1.不等式的基本性质有哪些?
2.解一元一次不等式与解一元一次方程,有哪些相同之处与不同之处?
3.应用一元一次不等式解决实际问题的一般步骤是什么?
4.如何确定一元一次不等式组的解集?
不等式:一般地,用符号“<”“>”“≤ ”“≥”表示大小关系的式子叫做不等式。 不等式的解:使不等式成立的未知数的值,叫做不等式的解。
不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。
一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
一元一次不等式组的解集:一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。 三、定理与性质 不等式的性质:
不等式的基本性质1:不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变。 不等式的基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。 不等式的基本性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
知识点
A
√
√
×
√
√
×
√
一元一次不等式的定义和性质
考点1
下列式子中,一元一次不等式有( )
①3x-1≥4
② 2+3x>6
③ 3- <5
④
⑤
⑥ x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
例1
【归纳拓展】一元一次不等式的概念含几个要点:
(1)用不等号连接;
(2)不等号两边都是关于未知数的整式;
(3)只含有一个未知数,且含有未知数的项的最高
次数为1.
【迁移应用1】
如果a
B.
C.
D.
B
解不等式,并把它们的解集在数轴上表示出来.
(1)3[x-2(x-2)]>x-3(x-2);
(2)
解:
(1)x<6,数轴上表示为
0
6
(2)y<2,数轴上表示为
0
2
解一元一次不等式
考点2
例2
【归纳拓展】解不等式一定要把握好基础知识:
①不等式的性质;②去分母,去括号,合并同类项.
熟练掌握并利用这些基础知识解题,保证准确率.
【迁移应用2】
不等式4x-6 ≥7x-12的非负整数解为 .
0,1,2
小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
分析:从路程下手找不等关系:
即小亮40分钟行进路程≥小明从8时20分到11时行进路程.
解:设小亮的速度为x千米/时,40分= 小时,
列不等式,得 ,解得x≥16.
小亮的速度至少为16千米/时.
例3
一元一次不等式的应用
考点3
【迁移应用3】
当x ___ 时,代数式 的值不小于 的值,此时x的最小整数值是 .
【归纳拓展】不等式的应用情况很多,但解所有的题目关键在于找准表示不等关系的语句,并能够列出不等式,再利用不等式的性质解不等式,这样问题才能得以解决.
≥-0.75
0
已知不等式组 有解,则a的取值范围为
( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
解析:解不等式x-a≥0,得x≥a;解不等式-2x>-4,得x<2.因为不等式组有解,故2在a的右边,即a<2.
一元一次不等式组的定义与解集
考点4
例4
【归纳拓展】不等式组的解集确定方法除利用数轴直观确定外,还可以用口诀确定:同大取大,同小取小,大小小大中间找,大大小小没得找.
【迁移应用4】
下列说法中,正确的个数是( )
①x=7是不等式组 的解;②不等式组 的解集是
-2≤x<3; ③不等式组 的解集是x=6; ④关于x的不等式组
无解.
x>1
x>-1
x>3
x≥-2
x≥6
x≤6
x>4
x<2
A.1个 B.2个 C.3个 D.4个
C
解不等式组:
①
②
解:①不等式组的解集是 ;
②不等式组的解集是x≥9.
例5
解一元一次不等式组
考点5
【归纳拓展】解不等式组的基础是解不等式,把每个不等式的解集解出来后,按求不等式组解集的口诀或利用画数轴的方法找到解集.
【迁移应用5】
不等式组 的所有整数解的和是 .
2x-1>1,
-4x≥-2x-8
提示:不等式组的解集是1
一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5
小朋友有6人,玩具有22件;或小朋友有7人,玩具有25件;或小朋友有8人,玩具有28件.
用一元一次不等式组解决实际问题
考点6
例6
【归纳拓展】当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属于通过列不等式(组)来解决的问题,而不属于通过列方程(组)来解决的问题.
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
课后训练
1.已知点M(3a-9,1-a)在第三象限,且它的横、纵坐标都
是整数,则a的值是( )
A. 1 B. 2 C. 3 D. 0
2.关于x的不等式x-2a≤1的解集如图所示,则a的值是 .
-1
0
1
B
-1
4.解不等式组: ,并把解集在数轴上表
示出来.
3.解不等式
解:x ≤8
解:1
