人教版数学七年级下册第九章9.3一元一次不等式组巩固与提高课件 (24张PPT)
文档属性
| 名称 | 人教版数学七年级下册第九章9.3一元一次不等式组巩固与提高课件 (24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 235.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 09:03:08 | ||
图片预览








文档简介
七年级下册第九章不等式与不等式组
9.3一元一次不等式组巩固与提高
知识改变命运
目标要求
1.认识一元一次不等式组,掌握一元一次不等式组的解法.
2.理解不等式组解集的概念,会解与不等式组解集有关的问题.
重难点
重点:一元一次不等式组的解法.
难点:确定一元一次不等式组的解集.
概 念
1、一元一次不等式组
把含有相同未知数的几个一元一次不等式联立起来,就组成了一元一次不等式组。
2、不等式组的解集
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
3、解不等式组
求不等式组解集的过程,叫做解不等式组。
4、一元一次不等式组的解法
①求出每个一元一次不等式的解集;②求出这些解集的公共部分,便得到一元一次不等式组的解集.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一元一次不等式组
解集
图示
语言表达
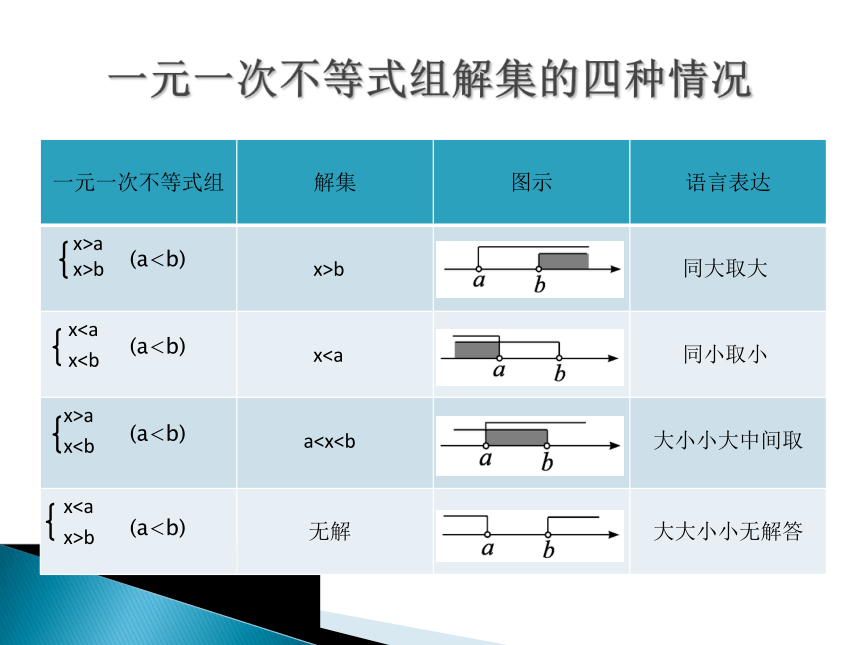
x>a
x>b
x>b
同大取大
x x x 同小取小
x>a
x a 大小小大中间取
x x>b
无解
大大小小无解答
一元一次不等式组解集的四种情况
(a(a(a(a 例1:解下列不等式组.
2x+1>-3 2x+3<9-x
8-2x≤x-1 2x-5>3x
解不等式组时,要先分别求出不等式组中每个不等式的解集,然后画数轴,找它们解集的公共部分,这个公共部分就是不等式的解集.
(1)解不等式①,得x>-2,
解不等式②,得x≥3.
所以,原不等式组的解集为x≥3,
解集表示在数轴上为图1。
(2)解不等式①,得x<2,
解不等式②,得x<-5,
所以,原不等式组的解集为x<-5.
其解集在数轴上表示如图2.
(3) (4)
3x+117x-15>13x-7
(3)解不等式①,得x<-2,
解不等式②,得x≥-5,
不等式组的解集为-5≤x<-2.
其解集在数轴上表示如图(3).
(4)解不等式①,得x>2,
解不等式②,得x<-1.
不等式的解集无公共部分,故这个不等式组无解.
把①、②的解集在数轴上表示如图(4).
例2:若关于x的不等式组 的整数解只有3个,则a的取值范围是( )
一元一次不等式组的整数解
5≤a<6
求每一个不等式的解集,得出不等式组的解集,再结合不等式组整数解的个数可确定a的范围。
解:解不等式x-a≤a,得:x≤a,
解不等式5-2x<1,得:x>2,
则不等式组的解集为2<x≤a,
因为不等式组的整数解只有3个,
所以5≤a<6,
数轴法
练一练1:
关于x的不等式组 恰好只有4个整数解,
则a的取值范围为( )
一元一次不等式组的整数解
-2≤a<-1
解:不等式组整理得
解得:
解集中恰好只有4个整数解,得到整数解为0,1,2,3
∴-1≤a+1<0,
解得:-2≤a<-1
例3:已知关于x,y的方程组 的解满
足不等式组 ,求满足条件的m的整数值
一元一次不等式组的整数解
关键是用含m的式子表示x、y
解:①+②得:3x+y=3m+4,
②-①得:x+5y=m+4,
因为不等式组
所以
解得不等式组
m =-3 -2
练一练3—1
若方程组 ,解集满足x>-1且y<-1,
求k的整数解.
解:
①+②得:2x=k+1
①-② 2y=3k-1
方程组,解集满足x>-1且y<-1
解得:-3<k<-1/3
k的整数解是-2,-1
②
①
例4:阳光学校计划购买篮球和足球共50个,购买资金不超过3200元,且购买篮球的数量不少于足球数量的一半,若每个篮球80元,每个足球50元.求共有几种购买方案?设购买篮球x个,可列不等式组( )
一元一次不等式组的应用
根据购买篮球的数量不少于足球数量的一半
总价=单价×购买数量结合购买资金不超过3200元
找数量关系
解:设购买篮球x个,则购买足球(50-x)个
例5:八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设同学人数为x人,下列各项能准确的求出同学人数与种植的树木的数量的是( )
一元一次不等式组的应用
理解“有1位同学植树的棵数不到8棵”
找数量关系
例6:根据“x的2倍大于4,且x的三分之一与1的
和不大于2”列出的不等式组是 ( )
一元一次不等式组的应用
把文字语言的不等关系转化为用数学符号表示的不等式
解:根据题意可列不等式组为
1、a与5的和是正数且a的一半不大于3”用不等式组表示 ( )
2、x的5倍与4的和大于3,且x的2倍是非负数,列不等组为( )
巩固练习
3、我市某学校有住宿生若干名,分住若干间宿舍,若每间住4人,则还有19人无宿舍住;若每间住7人,则有一间宿舍不空但所住的人数不足5人.若设宿舍间数为x,根据题意x应满足的不等式(组)为( )
例7:按如图的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否>487?”为一次操作.如果操作进行四次才停止,那么x的取值范围
( )
解:前四次操作的结果分别为
3x-2;
3(3x-2)-2=9x-8;
3(9x-8)-2=27x-26;
3(27x-26)-2=81x-80;
列不等式组
解得: 7<x≤19
7<x≤19
练一练:如图,这是李强同学设计的一个计算机程序,规定从“输入一个值x”到判断“结果是否≥15”为一次运行过程.如果程序运行两次就停止,那么x的取值范围是( )
解:依题意,得
解得:3≤x<7
3≤x<7
例8:科学商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )
解:设该店购进甲种商品x件,则购进乙种商品(50-x)件,
解得:20≤x<25
∵ x为整数,
∴ x=20、21、22、23、24,
∴ 该店进货方案有5种,
5
例9:第二届“一带一路”国际合作高峰论坛将于2019年4月在北京举行.为了让恩施特产走出大山,走向世界,恩施一民营企业计划生产甲、乙两种商品共10万件,销住“一带一路”沿线国家和地区.已知3件甲种商品与2件乙种商品的销售收入相同,1件甲种商品比2件乙种商品的销售收入少600元.甲、乙两种商品的销售利润分别为120元和200元
(1)甲、乙两种商品的销售单价各多少元?
(2)市场调研表明:所有商品能全部售出,企业要求生产乙种商品的数量不超过甲种商品数量的2/3,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
解:
(1)设甲种商品的销售单价x元,乙种商品的销售单价y元.
解得
答:甲种商品的销售单价是300元,乙种商品的单价为450元
(2)设生产甲种商品a万件,则生产乙种商品(10-a)万件
解得6≤a≤8,
∵乙种商品的销售利润比甲种商品的销售利润高,
∴乙种商品销售越多,销售总利润就越大,
∴当生产甲种商品6万件,则生产乙种商品4万件时销售总利润最大.
销售总利润为:60000×120+40000×200=15200000(元).
答:该企业生产甲种商品6万件,则生产乙种商品4万件时销售总利润最大,最大利润为15200000元.
本节课我们学习了一元一次不等式组的有关概念和解法,在确定解集时常用“数轴法”或“口诀法”.
本节小结
家庭作业
请完成课后相关练习。
9.3一元一次不等式组巩固与提高
知识改变命运
目标要求
1.认识一元一次不等式组,掌握一元一次不等式组的解法.
2.理解不等式组解集的概念,会解与不等式组解集有关的问题.
重难点
重点:一元一次不等式组的解法.
难点:确定一元一次不等式组的解集.
概 念
1、一元一次不等式组
把含有相同未知数的几个一元一次不等式联立起来,就组成了一元一次不等式组。
2、不等式组的解集
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
3、解不等式组
求不等式组解集的过程,叫做解不等式组。
4、一元一次不等式组的解法
①求出每个一元一次不等式的解集;②求出这些解集的公共部分,便得到一元一次不等式组的解集.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一元一次不等式组
解集
图示
语言表达
x>a
x>b
x>b
同大取大
x x x 同小取小
x>a
x a
x x>b
无解
大大小小无解答
一元一次不等式组解集的四种情况
(a
2x+1>-3 2x+3<9-x
8-2x≤x-1 2x-5>3x
解不等式组时,要先分别求出不等式组中每个不等式的解集,然后画数轴,找它们解集的公共部分,这个公共部分就是不等式的解集.
(1)解不等式①,得x>-2,
解不等式②,得x≥3.
所以,原不等式组的解集为x≥3,
解集表示在数轴上为图1。
(2)解不等式①,得x<2,
解不等式②,得x<-5,
所以,原不等式组的解集为x<-5.
其解集在数轴上表示如图2.
(3) (4)
3x+1
(3)解不等式①,得x<-2,
解不等式②,得x≥-5,
不等式组的解集为-5≤x<-2.
其解集在数轴上表示如图(3).
(4)解不等式①,得x>2,
解不等式②,得x<-1.
不等式的解集无公共部分,故这个不等式组无解.
把①、②的解集在数轴上表示如图(4).
例2:若关于x的不等式组 的整数解只有3个,则a的取值范围是( )
一元一次不等式组的整数解
5≤a<6
求每一个不等式的解集,得出不等式组的解集,再结合不等式组整数解的个数可确定a的范围。
解:解不等式x-a≤a,得:x≤a,
解不等式5-2x<1,得:x>2,
则不等式组的解集为2<x≤a,
因为不等式组的整数解只有3个,
所以5≤a<6,
数轴法
练一练1:
关于x的不等式组 恰好只有4个整数解,
则a的取值范围为( )
一元一次不等式组的整数解
-2≤a<-1
解:不等式组整理得
解得:
解集中恰好只有4个整数解,得到整数解为0,1,2,3
∴-1≤a+1<0,
解得:-2≤a<-1
例3:已知关于x,y的方程组 的解满
足不等式组 ,求满足条件的m的整数值
一元一次不等式组的整数解
关键是用含m的式子表示x、y
解:①+②得:3x+y=3m+4,
②-①得:x+5y=m+4,
因为不等式组
所以
解得不等式组
m =-3 -2
练一练3—1
若方程组 ,解集满足x>-1且y<-1,
求k的整数解.
解:
①+②得:2x=k+1
①-② 2y=3k-1
方程组,解集满足x>-1且y<-1
解得:-3<k<-1/3
k的整数解是-2,-1
②
①
例4:阳光学校计划购买篮球和足球共50个,购买资金不超过3200元,且购买篮球的数量不少于足球数量的一半,若每个篮球80元,每个足球50元.求共有几种购买方案?设购买篮球x个,可列不等式组( )
一元一次不等式组的应用
根据购买篮球的数量不少于足球数量的一半
总价=单价×购买数量结合购买资金不超过3200元
找数量关系
解:设购买篮球x个,则购买足球(50-x)个
例5:八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设同学人数为x人,下列各项能准确的求出同学人数与种植的树木的数量的是( )
一元一次不等式组的应用
理解“有1位同学植树的棵数不到8棵”
找数量关系
例6:根据“x的2倍大于4,且x的三分之一与1的
和不大于2”列出的不等式组是 ( )
一元一次不等式组的应用
把文字语言的不等关系转化为用数学符号表示的不等式
解:根据题意可列不等式组为
1、a与5的和是正数且a的一半不大于3”用不等式组表示 ( )
2、x的5倍与4的和大于3,且x的2倍是非负数,列不等组为( )
巩固练习
3、我市某学校有住宿生若干名,分住若干间宿舍,若每间住4人,则还有19人无宿舍住;若每间住7人,则有一间宿舍不空但所住的人数不足5人.若设宿舍间数为x,根据题意x应满足的不等式(组)为( )
例7:按如图的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否>487?”为一次操作.如果操作进行四次才停止,那么x的取值范围
( )
解:前四次操作的结果分别为
3x-2;
3(3x-2)-2=9x-8;
3(9x-8)-2=27x-26;
3(27x-26)-2=81x-80;
列不等式组
解得: 7<x≤19
7<x≤19
练一练:如图,这是李强同学设计的一个计算机程序,规定从“输入一个值x”到判断“结果是否≥15”为一次运行过程.如果程序运行两次就停止,那么x的取值范围是( )
解:依题意,得
解得:3≤x<7
3≤x<7
例8:科学商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )
解:设该店购进甲种商品x件,则购进乙种商品(50-x)件,
解得:20≤x<25
∵ x为整数,
∴ x=20、21、22、23、24,
∴ 该店进货方案有5种,
5
例9:第二届“一带一路”国际合作高峰论坛将于2019年4月在北京举行.为了让恩施特产走出大山,走向世界,恩施一民营企业计划生产甲、乙两种商品共10万件,销住“一带一路”沿线国家和地区.已知3件甲种商品与2件乙种商品的销售收入相同,1件甲种商品比2件乙种商品的销售收入少600元.甲、乙两种商品的销售利润分别为120元和200元
(1)甲、乙两种商品的销售单价各多少元?
(2)市场调研表明:所有商品能全部售出,企业要求生产乙种商品的数量不超过甲种商品数量的2/3,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
解:
(1)设甲种商品的销售单价x元,乙种商品的销售单价y元.
解得
答:甲种商品的销售单价是300元,乙种商品的单价为450元
(2)设生产甲种商品a万件,则生产乙种商品(10-a)万件
解得6≤a≤8,
∵乙种商品的销售利润比甲种商品的销售利润高,
∴乙种商品销售越多,销售总利润就越大,
∴当生产甲种商品6万件,则生产乙种商品4万件时销售总利润最大.
销售总利润为:60000×120+40000×200=15200000(元).
答:该企业生产甲种商品6万件,则生产乙种商品4万件时销售总利润最大,最大利润为15200000元.
本节课我们学习了一元一次不等式组的有关概念和解法,在确定解集时常用“数轴法”或“口诀法”.
本节小结
家庭作业
请完成课后相关练习。
