人教版七年级数学下册:5.1.1相交线 课件 (共19张PPT)
文档属性
| 名称 | 人教版七年级数学下册:5.1.1相交线 课件 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 903.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览



文档简介
相交线与对顶角
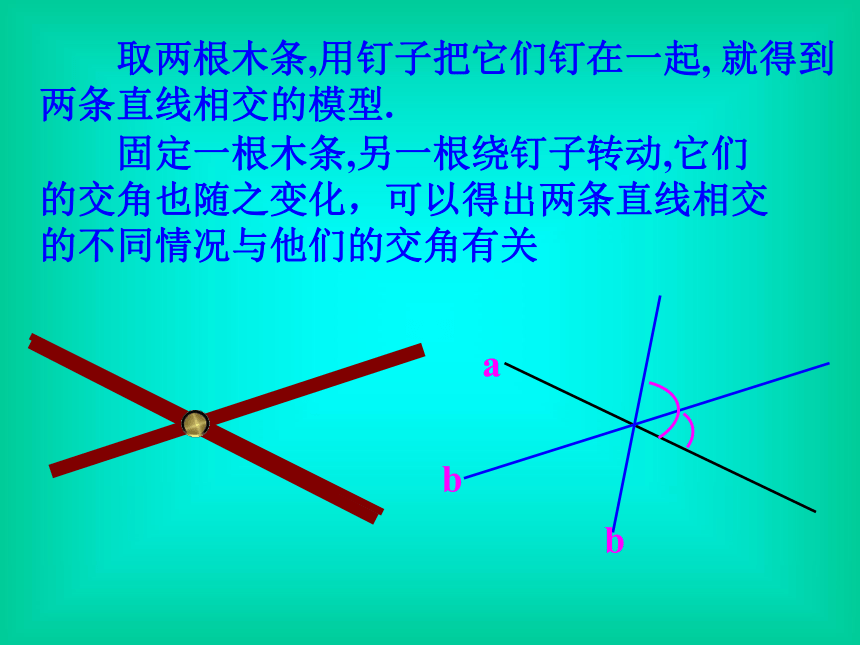
取两根木条,用钉子把它们钉在一起, 就得到两条直线相交的模型.
a
b
固定一根木条,另一根绕钉子转动,它们的交角也随之变化,可以得出两条直线相交的不同情况与他们的交角有关
b
1、对顶角的概念
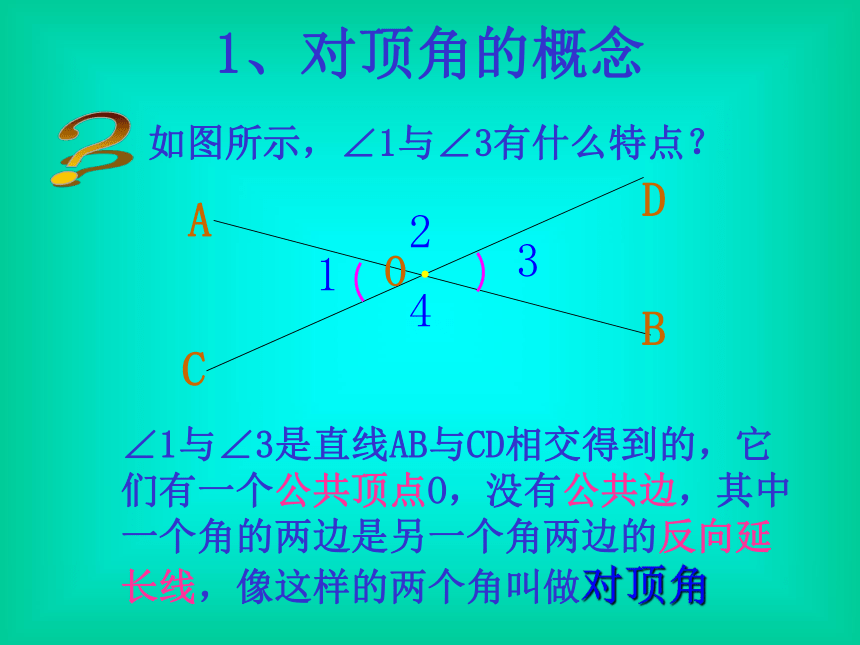
如图所示,∠1与∠3有什么特点?
∠1与∠3是直线AB与CD相交得到的,它们有一个公共顶点O,没有公共边,其中一个角的两边是另一个角两边的反向延长线,像这样的两个角叫做对顶角
2
3
1
4
A
B
C
D
O
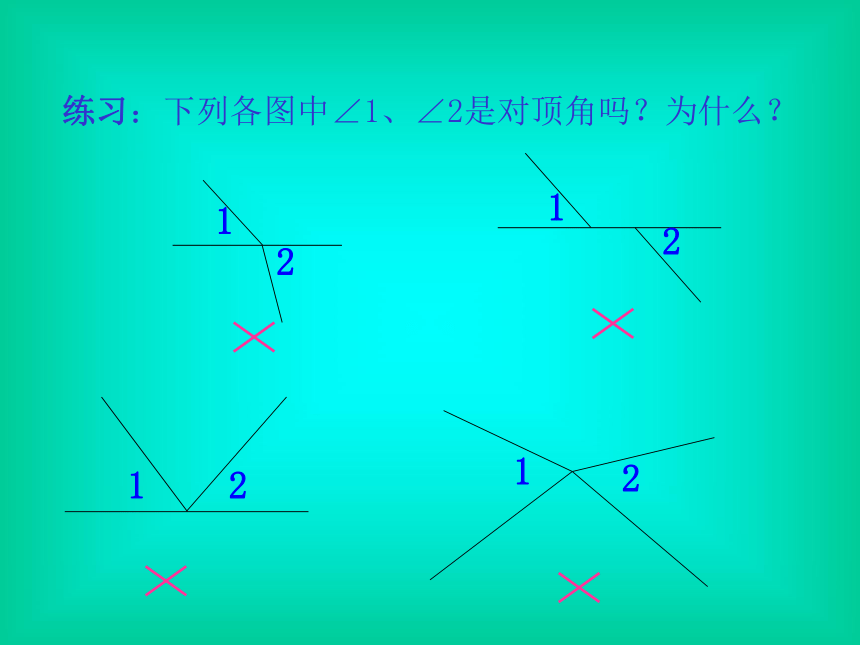
练习:下列各图中∠1、∠2是对顶角吗?为什么?
1
2
1
2
2
1
1
2
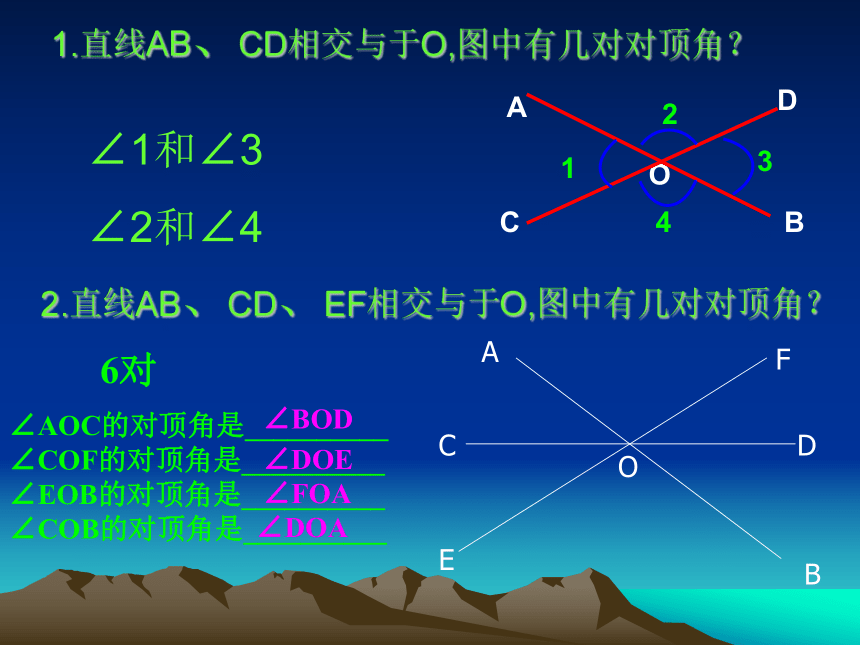
1.直线AB、CD相交与于O,图中有几对对顶角?
O
A
B
C
D
1
2
3
4
∠1和∠3
∠2和∠4
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
A
B
C
D
E
F
O
∠AOC的对顶角是__________
∠COF的对顶角是__________
∠EOB的对顶角是__________
∠COB的对顶角是__________
6对
∠BOD
∠DOE
∠FOA
∠DOA
2、邻补角的概念
∠1和∠2与对顶角相比,有什么相同点和不同点?
∠1和∠2也是直线AB、CD相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,且另一边在同一直线上.像这样的两个角叫做邻补角。
2
3
1
4
A
B
C
D
O
显然:两个邻补角的和为180度
练习:下列各图中∠1、∠2是邻补角吗?为什么?
1
2
1
2
1
2
邻补角的基本图形
1
2
观察、讨论
1、如图直线AB、CD相交于点O,说出图中有几个角?几对邻补角?
O
A
B
C
D
1
2
3
4
∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1
2.直线AB、CD、EF相交与于O,图中有几对邻补角?
A
B
C
D
E
F
O
∠AOC的邻补角是_________
∠COF的邻补角是_________
∠EOB的邻补角是_________
∠COB 、∠AOD
∠FOD 、∠COE
∠AOE 、∠BOF
3、对顶角的性质
4
2
3
1
A
B
C
D
O
对顶角的性质:对顶角相等。
∵
∠1+ ∠2=
∠2+ ∠3=
∴
∠1= ∠3
180°
180°
这个推理过程还可以写成:
∵ ∠1与∠2互补, ∠3与∠2互补(邻补角定义)
∴ ∠ 1= ∠3(同角的补角相等)
例题1
已知:直线a,b相交,∠1=400
求∠2、∠3、∠4的度数?
a
b
1
2
3
4
解:∠3=∠1=400 (对顶角相等)
∠2=1800-∠1=1800-400=1400
(邻补角的定义)
∠4=∠2=1400(对顶角相等)
变式练习
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
a
b
1
2
3
4
练习
2、如图所示,三条直线AB、CD、EF相交于O点,∠1=400, ∠2=750,则∠3等于多少度?
1、两条直线相交得4个角,其中一个角是900,其余各角是多少度?
A
B
C
1
2
3
O
D
E
F
练习
1、下列说法正确的有( )
A、相等的角是对顶角
B、不是对顶角的角不相等
C、对顶角必相等
D、有公共顶点的角是对顶角
E 、邻补角的和一定是180度
F、互补的两个角一定是邻补角
G、两条直线相交,只要其中一个角的大小确定了,
那么另外三个角的大小就确定了
C、E、G
归纳小结
①两条直线相交形成的角
②有一个公共顶点;
③没有公共边
①两条直线相交而成;
②有一个公共点;
③有一条公共边
对顶
角相
等
角的名称 特 征 性 质 相 同 点 不 同 点
对顶角
邻补角
邻补
角互
补
①都是两条直线相交而成的 角;
②都有一个公共顶点;
③都是成对出现的
①有无公共边
②两直线相交时,
对顶角只有一对
邻补角有两个
举出生活中相交线的例子
这节课的主要收获
如何判断两个角是对顶角?邻补角?
对顶角的判断 邻补角的判断
对顶角、邻补角的性质
对顶角的性质:对顶角相等
邻补角的性质:邻补角互补
(位置关系)
(数量关系)
取两根木条,用钉子把它们钉在一起, 就得到两条直线相交的模型.
a
b
固定一根木条,另一根绕钉子转动,它们的交角也随之变化,可以得出两条直线相交的不同情况与他们的交角有关
b
1、对顶角的概念
如图所示,∠1与∠3有什么特点?
∠1与∠3是直线AB与CD相交得到的,它们有一个公共顶点O,没有公共边,其中一个角的两边是另一个角两边的反向延长线,像这样的两个角叫做对顶角
2
3
1
4
A
B
C
D
O
练习:下列各图中∠1、∠2是对顶角吗?为什么?
1
2
1
2
2
1
1
2
1.直线AB、CD相交与于O,图中有几对对顶角?
O
A
B
C
D
1
2
3
4
∠1和∠3
∠2和∠4
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
A
B
C
D
E
F
O
∠AOC的对顶角是__________
∠COF的对顶角是__________
∠EOB的对顶角是__________
∠COB的对顶角是__________
6对
∠BOD
∠DOE
∠FOA
∠DOA
2、邻补角的概念
∠1和∠2与对顶角相比,有什么相同点和不同点?
∠1和∠2也是直线AB、CD相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,且另一边在同一直线上.像这样的两个角叫做邻补角。
2
3
1
4
A
B
C
D
O
显然:两个邻补角的和为180度
练习:下列各图中∠1、∠2是邻补角吗?为什么?
1
2
1
2
1
2
邻补角的基本图形
1
2
观察、讨论
1、如图直线AB、CD相交于点O,说出图中有几个角?几对邻补角?
O
A
B
C
D
1
2
3
4
∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1
2.直线AB、CD、EF相交与于O,图中有几对邻补角?
A
B
C
D
E
F
O
∠AOC的邻补角是_________
∠COF的邻补角是_________
∠EOB的邻补角是_________
∠COB 、∠AOD
∠FOD 、∠COE
∠AOE 、∠BOF
3、对顶角的性质
4
2
3
1
A
B
C
D
O
对顶角的性质:对顶角相等。
∵
∠1+ ∠2=
∠2+ ∠3=
∴
∠1= ∠3
180°
180°
这个推理过程还可以写成:
∵ ∠1与∠2互补, ∠3与∠2互补(邻补角定义)
∴ ∠ 1= ∠3(同角的补角相等)
例题1
已知:直线a,b相交,∠1=400
求∠2、∠3、∠4的度数?
a
b
1
2
3
4
解:∠3=∠1=400 (对顶角相等)
∠2=1800-∠1=1800-400=1400
(邻补角的定义)
∠4=∠2=1400(对顶角相等)
变式练习
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
a
b
1
2
3
4
练习
2、如图所示,三条直线AB、CD、EF相交于O点,∠1=400, ∠2=750,则∠3等于多少度?
1、两条直线相交得4个角,其中一个角是900,其余各角是多少度?
A
B
C
1
2
3
O
D
E
F
练习
1、下列说法正确的有( )
A、相等的角是对顶角
B、不是对顶角的角不相等
C、对顶角必相等
D、有公共顶点的角是对顶角
E 、邻补角的和一定是180度
F、互补的两个角一定是邻补角
G、两条直线相交,只要其中一个角的大小确定了,
那么另外三个角的大小就确定了
C、E、G
归纳小结
①两条直线相交形成的角
②有一个公共顶点;
③没有公共边
①两条直线相交而成;
②有一个公共点;
③有一条公共边
对顶
角相
等
角的名称 特 征 性 质 相 同 点 不 同 点
对顶角
邻补角
邻补
角互
补
①都是两条直线相交而成的 角;
②都有一个公共顶点;
③都是成对出现的
①有无公共边
②两直线相交时,
对顶角只有一对
邻补角有两个
举出生活中相交线的例子
这节课的主要收获
如何判断两个角是对顶角?邻补角?
对顶角的判断 邻补角的判断
对顶角、邻补角的性质
对顶角的性质:对顶角相等
邻补角的性质:邻补角互补
(位置关系)
(数量关系)
