鲁教版(五四制)八年级上册第五章平行四边形单元测试卷(Word版 含答案)
文档属性
| 名称 | 鲁教版(五四制)八年级上册第五章平行四边形单元测试卷(Word版 含答案) | 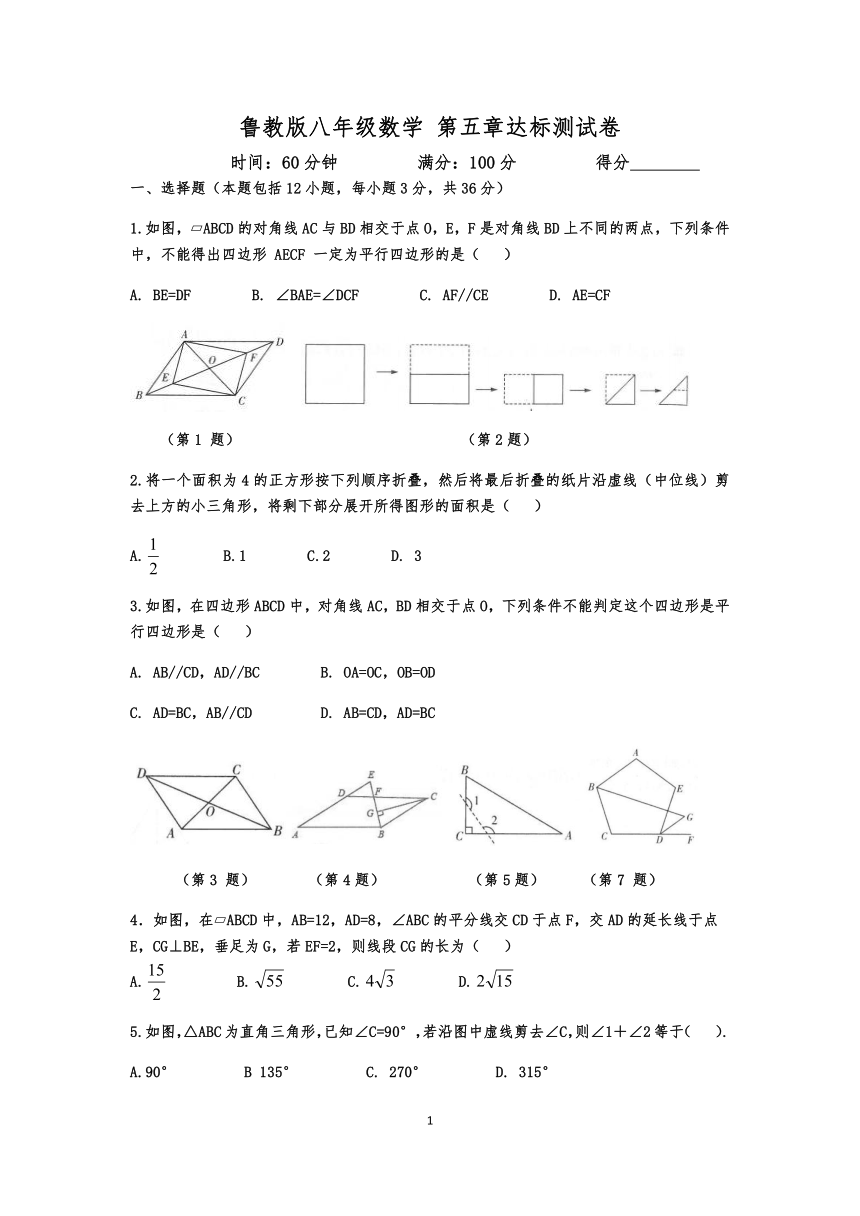 | |
| 格式 | zip | ||
| 文件大小 | 482.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 07:56:14 | ||
图片预览




文档简介
鲁教版八年级数学
第五章达标测试卷
时间:60分钟
满分:100分
得分
一、选择题(本题包括12小题,每小题3分,共36分)
1.如图,?ABCD的对角线AC与BD相交于点O,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形
AECF
一定为平行四边形的是(
)
A.
BE=DF
B.
∠BAE=∠DCF
C.
AF//CE
D.
AE=CF
(第1
题)
(第2题)
2.将一个面积为4的正方形按下列顺序折叠,然后将最后折叠的纸片沿虚线(中位线)剪去上方的小三角形,将剩下部分展开所得图形的面积是(
)
A.
B.1
C.2
D.
3
3.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形是(
)
A.
AB//CD,AD//BC
B.
OA=OC,OB=OD
C.
AD=BC,AB//CD
D.
AB=CD,AD=BC
(第3
题)
(第4题)
(第5题)
(第7
题)
4.如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点
E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为(
)
A.
B.
C.
D.
5.如图,△ABC为直角三角形,已知∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于(
).
A.90°
B
135°
C.
270°
D.
315°
6.从一个十边形的某个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成(
)个三角形。
A.10
B.
9
C.8
D.
7
7.
如图,在正五边形
ABCDE中,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G的度数为(
)
A.36°
B.54°
C.60°
D.72°
8.如图,甲、∠两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
(甲)连接BD,CE,两线段相交于点
P,则
P
即为所求;
(∠)先取CD的中点M,再以A为圆心,AB长为半径画弧,交AM于P点,则P即为所求.
对于甲、∠两人的作法,下列判断正确的是(
)
A.两人皆正确
B.两人皆错误
C.甲正确,∠错误
D.甲错误,∠正确
(第8
题)
(第9
题)
(第
10
题)
9.如图,在△ABC中,D,E,F分别为
BC,AC,AB边的中点,AH⊥BC于点H,FD=16,则HE等于(
)
A.
32
B.
16
C.
8
D.
10
10.如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:
BE=1:3;③BE:BG=4:3,其中正确的是(
)
A.
①②③
B.
①②
C.
②③
D.
①③
11.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF
的周长为(
)
A.8
B.
10
C.12
D.16
(第11
题)
(第12
题)
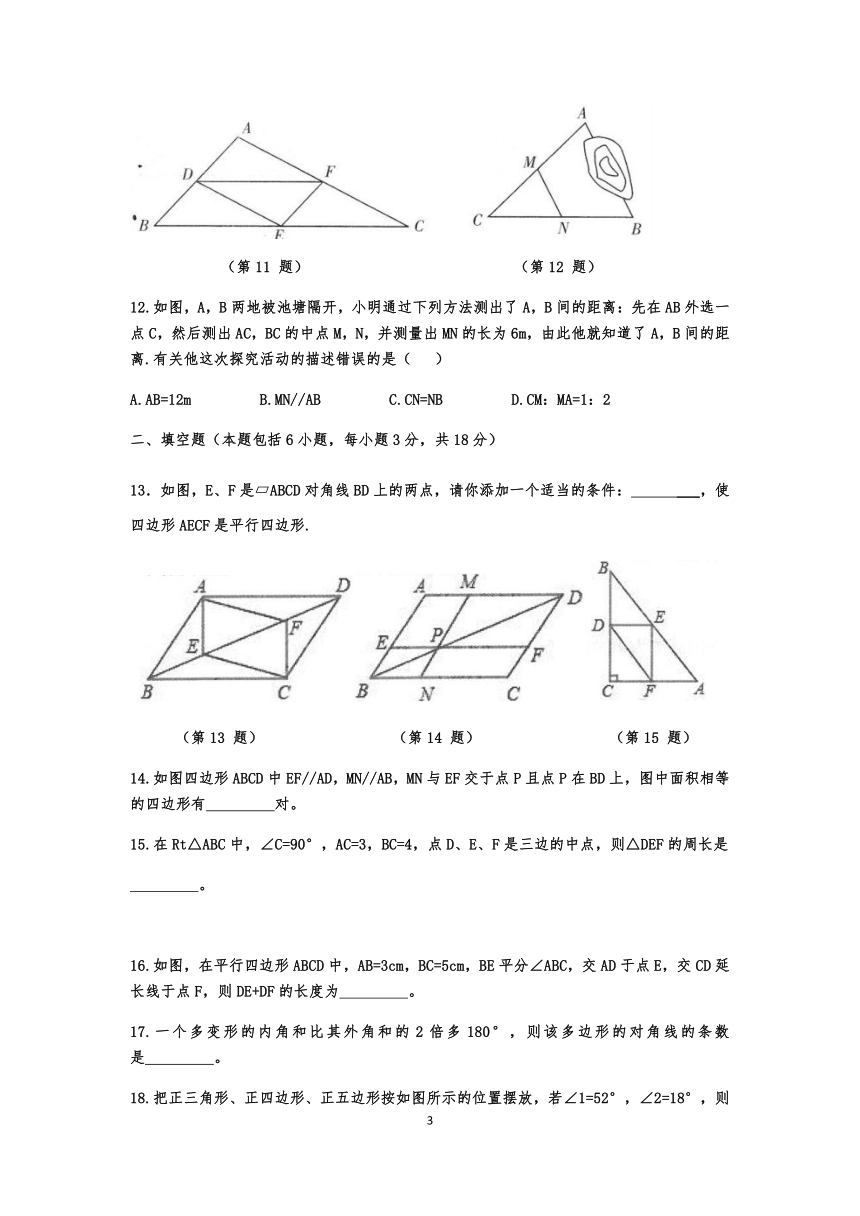
12.如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是(
)
A.AB=12m
B.MN//AB
C.CN=NB
D.CM:MA=1:2
二、填空题(本题包括6小题,每小题3分,共18分)
13.如图,E、F是?ABCD对角线BD上的两点,请你添加一个适当的条件:
___,使四边形AECF是平行四边形.
(第13
题)
(第14
题)
(第15
题)
14.如图四边形ABCD中EF//AD,MN//AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有
对。
15.在Rt△ABC中,∠C=90°,AC=3,BC=4,点D、E、F是三边的中点,则△DEF的周长是
。
16.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为
。
17.一个多变形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是
。
18.把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=
。
(第16
题)
(第18
题)
三、解答题(本题包括5小题,共46分)
19.(6分)如图,已知E,F是?ABCD对角线AC上的两点,并且AE=CF.请说明四边形BFDE是平行四边形.
20.(9分)如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.(1)求证:CD=BE;
(2)若点F为DC的中点,DG⊥AE
于点G,且DG=1,AB=4,求AE的长.
21.(9分)如图,在?ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.求证:
(1)△AEM≌△CFN;
(2)四边形BMDN是平行四边形.
22.(10分)如图,在△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD
点F,E是AB的中点.
(1)求证:EF//BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
23.(12分)在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图(1),BE的延长线与AC边相交于点D,求证:;
(2)如图(2),在△ABC中,AB=9,AC=5,求线段EF的长.
第五章达标测试卷
参考答案
一、选择题(本题包括12小题,每小题3分,共36分)
序号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
C
D
C
C
B
C
B
D
D
D
二、填空题(本题包括6小题,每小题3分,共18分)
13.BE=DF或∠ABE=∠CDF
14.5
15.6
16.4cm
17.7
18.32°
三、解答题(本题包括5小题,共46分)
19.解答过程
∵四边形ABCD是平行四边形
∴AD=BC,AD//BC
∴∠DAE=∠BCF
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS)
∴DE=BF,∠DEA=∠BFC
∴∠DEF=∠BFE
∴DE//BF
∴四边形BFDE是平行四边形
20.解答过程
(1)证明:
∵AE为∠ADB的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD//BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)四边形ABCD是平行四边形,
∴CD//AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
F为DC的中点,AB=4,
∴DF=CF=DA=2.
∴DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=.
在△ADF和△ECF中∠DAF=∠E,∠ADF=∠ECF,
DP=CF
△ADF≌△ECF(AAS).
∴AF=EF,
AE=2AF=.
21.解答过程
证明:(1)
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
∵AD//BC,
∴∠E=∠F.
在△AEM与△CFN中,
∠EAM=∠FCN,AE=CF,∠E=∠F
∴△AEM≌△CFN(ASA)
(2)∵四边形ABCD是平行四边形,∴AB=CD,AB//CD
又由(1)得AM=CN,∴BM=DN,BM//DN,∴四边形BMDN是平行四边形.
22.解答过程
(1)∵CA=CD,CF平分∠ACB
∴CF是AD边的中线,
∵E是AB的中点,
∴EF是△ABD的中位线,
∴EF//BD
(2)过点F作FM垂直于DC交DC于点M
∵CA=CD,CF平分∠ACB
∴CF⊥AD,
∵∠ACB=90°
∴∠FCD=30°
∵AC=DC=8,
∴FD=4,FC=,BD=BC-DC=4
∴FM=
∵EF是△ABD的中位线,
∴EF=BD=2
∴S四边形BDFE=(EF+BD)FM=×(2+4)×=
23.解答过程
(1)在△AEB和△AED中,
∴△AEB≌△AED(ASA)
∴BE=ED,AD=AB,
∵BE=ED,BF=FC,
∴EF=CD=(AC-AD)=(AC-AB)
;
(2)分别延长BE、AC交于点H,
在△AEB和△AEH中,
∴△AEB≌△AEH(ASA)
∴BE=EH,AH=AB=9,
∴BE=EH,BF=FC,
EF=CH=(AH-AC)=2.
第五章达标测试卷
时间:60分钟
满分:100分
得分
一、选择题(本题包括12小题,每小题3分,共36分)
1.如图,?ABCD的对角线AC与BD相交于点O,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形
AECF
一定为平行四边形的是(
)
A.
BE=DF
B.
∠BAE=∠DCF
C.
AF//CE
D.
AE=CF
(第1
题)
(第2题)
2.将一个面积为4的正方形按下列顺序折叠,然后将最后折叠的纸片沿虚线(中位线)剪去上方的小三角形,将剩下部分展开所得图形的面积是(
)
A.
B.1
C.2
D.
3
3.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形是(
)
A.
AB//CD,AD//BC
B.
OA=OC,OB=OD
C.
AD=BC,AB//CD
D.
AB=CD,AD=BC
(第3
题)
(第4题)
(第5题)
(第7
题)
4.如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点
E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为(
)
A.
B.
C.
D.
5.如图,△ABC为直角三角形,已知∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于(
).
A.90°
B
135°
C.
270°
D.
315°
6.从一个十边形的某个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成(
)个三角形。
A.10
B.
9
C.8
D.
7
7.
如图,在正五边形
ABCDE中,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G的度数为(
)
A.36°
B.54°
C.60°
D.72°
8.如图,甲、∠两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
(甲)连接BD,CE,两线段相交于点
P,则
P
即为所求;
(∠)先取CD的中点M,再以A为圆心,AB长为半径画弧,交AM于P点,则P即为所求.
对于甲、∠两人的作法,下列判断正确的是(
)
A.两人皆正确
B.两人皆错误
C.甲正确,∠错误
D.甲错误,∠正确
(第8
题)
(第9
题)
(第
10
题)
9.如图,在△ABC中,D,E,F分别为
BC,AC,AB边的中点,AH⊥BC于点H,FD=16,则HE等于(
)
A.
32
B.
16
C.
8
D.
10
10.如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:
BE=1:3;③BE:BG=4:3,其中正确的是(
)
A.
①②③
B.
①②
C.
②③
D.
①③
11.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF
的周长为(
)
A.8
B.
10
C.12
D.16
(第11
题)
(第12
题)
12.如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是(
)
A.AB=12m
B.MN//AB
C.CN=NB
D.CM:MA=1:2
二、填空题(本题包括6小题,每小题3分,共18分)
13.如图,E、F是?ABCD对角线BD上的两点,请你添加一个适当的条件:
___,使四边形AECF是平行四边形.
(第13
题)
(第14
题)
(第15
题)
14.如图四边形ABCD中EF//AD,MN//AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有
对。
15.在Rt△ABC中,∠C=90°,AC=3,BC=4,点D、E、F是三边的中点,则△DEF的周长是
。
16.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为
。
17.一个多变形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是
。
18.把正三角形、正四边形、正五边形按如图所示的位置摆放,若∠1=52°,∠2=18°,则∠3=
。
(第16
题)
(第18
题)
三、解答题(本题包括5小题,共46分)
19.(6分)如图,已知E,F是?ABCD对角线AC上的两点,并且AE=CF.请说明四边形BFDE是平行四边形.
20.(9分)如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.(1)求证:CD=BE;
(2)若点F为DC的中点,DG⊥AE
于点G,且DG=1,AB=4,求AE的长.
21.(9分)如图,在?ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.求证:
(1)△AEM≌△CFN;
(2)四边形BMDN是平行四边形.
22.(10分)如图,在△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD
点F,E是AB的中点.
(1)求证:EF//BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
23.(12分)在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图(1),BE的延长线与AC边相交于点D,求证:;
(2)如图(2),在△ABC中,AB=9,AC=5,求线段EF的长.
第五章达标测试卷
参考答案
一、选择题(本题包括12小题,每小题3分,共36分)
序号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
C
D
C
C
B
C
B
D
D
D
二、填空题(本题包括6小题,每小题3分,共18分)
13.BE=DF或∠ABE=∠CDF
14.5
15.6
16.4cm
17.7
18.32°
三、解答题(本题包括5小题,共46分)
19.解答过程
∵四边形ABCD是平行四边形
∴AD=BC,AD//BC
∴∠DAE=∠BCF
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS)
∴DE=BF,∠DEA=∠BFC
∴∠DEF=∠BFE
∴DE//BF
∴四边形BFDE是平行四边形
20.解答过程
(1)证明:
∵AE为∠ADB的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD//BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)四边形ABCD是平行四边形,
∴CD//AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
F为DC的中点,AB=4,
∴DF=CF=DA=2.
∴DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=.
在△ADF和△ECF中∠DAF=∠E,∠ADF=∠ECF,
DP=CF
△ADF≌△ECF(AAS).
∴AF=EF,
AE=2AF=.
21.解答过程
证明:(1)
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
∵AD//BC,
∴∠E=∠F.
在△AEM与△CFN中,
∠EAM=∠FCN,AE=CF,∠E=∠F
∴△AEM≌△CFN(ASA)
(2)∵四边形ABCD是平行四边形,∴AB=CD,AB//CD
又由(1)得AM=CN,∴BM=DN,BM//DN,∴四边形BMDN是平行四边形.
22.解答过程
(1)∵CA=CD,CF平分∠ACB
∴CF是AD边的中线,
∵E是AB的中点,
∴EF是△ABD的中位线,
∴EF//BD
(2)过点F作FM垂直于DC交DC于点M
∵CA=CD,CF平分∠ACB
∴CF⊥AD,
∵∠ACB=90°
∴∠FCD=30°
∵AC=DC=8,
∴FD=4,FC=,BD=BC-DC=4
∴FM=
∵EF是△ABD的中位线,
∴EF=BD=2
∴S四边形BDFE=(EF+BD)FM=×(2+4)×=
23.解答过程
(1)在△AEB和△AED中,
∴△AEB≌△AED(ASA)
∴BE=ED,AD=AB,
∵BE=ED,BF=FC,
∴EF=CD=(AC-AD)=(AC-AB)
;
(2)分别延长BE、AC交于点H,
在△AEB和△AEH中,
∴△AEB≌△AEH(ASA)
∴BE=EH,AH=AB=9,
∴BE=EH,BF=FC,
EF=CH=(AH-AC)=2.
