苏科版九年级下册数学 7.5解直角三角形 同步练习(word解析版)
文档属性
| 名称 | 苏科版九年级下册数学 7.5解直角三角形 同步练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 228.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 22:15:25 | ||
图片预览




文档简介
7.5解直角三角形
同步练习
一.选择题
1.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A.
B.
C.
D.
2.如图,A、B、C分别是小正方形的三个顶点,且每个小正方形的边长均为1,则sin∠BAC的值为( )
A.
B.
C.1
D.
3.如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是BC上一点,若tan∠DAB=,则AD的长为( )
A.2
B.
C.2
D.8
4.如图,延长Rt△ABC的斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA的值是( )
A.1
B.
C.9
D.
5.如图,在△ABC中,∠ACB=90°,sinA=,CD平分∠ACB,则∠BDC的度数是( )
A.45°
B.60°
C.70°
D.75°
6.如图,在平面直角坐标系中,直线OA过点(4,2),则tanα的值是( )
A.
B.
C.
D.2
7.如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=3,tan∠BCE=,那么CE等于( )
A.2
B.3﹣2
C.5
D.4
8.将一副三角板如图摆放在一起,组成四边形ABCD,连接AC,则tan∠ACD的值等于( )
A.2
B.2+
C.1+
D.2
9.如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )
A.m=n
B.x=m+n
C.x>m+n
D.x2=m2+n2
10.如图,△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,则cos∠BPC=( )
A.
B.
C.
D.
二.填空题
11.在△ABC中,AB=AC,若cosA=,则=
.
12.在Rt△ABC中,∠B=90°,AC=5,BC=3,P为线段AB上一点,且CP=,则sin∠PCA的值为
.
13.如图,在△ABC中,AB=AC,sinB=,延长BC至点D,使CD:AC=1:3,则tan∠CAD=
.
14.已知在△ABC中,tanB=,BC=6,过点A作BC边上的高,垂足为D,且=2,则△ABC的面积为
.
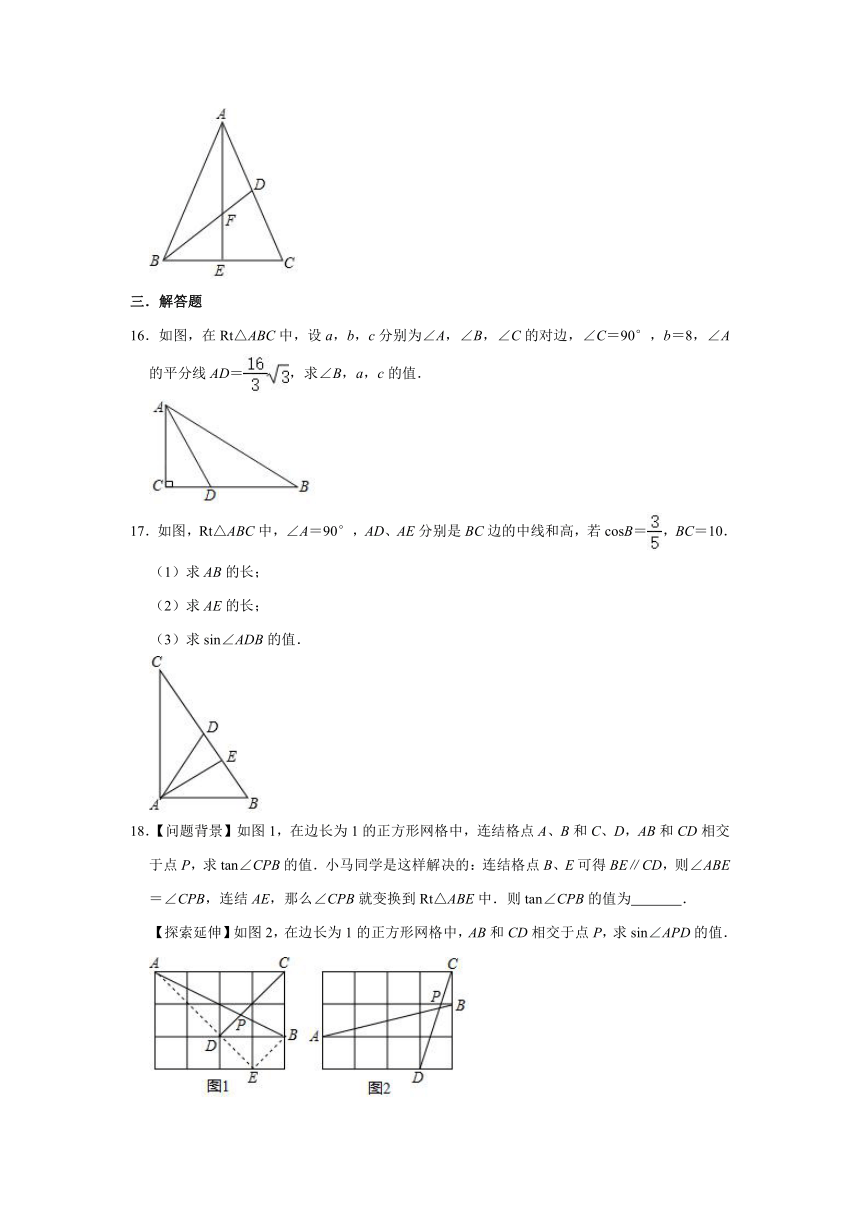
15.如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=,AB=13.则tan∠DBC的值为
.
三.解答题
16.如图,在Rt△ABC中,设a,b,c分别为∠A,∠B,∠C的对边,∠C=90°,b=8,∠A的平分线AD=,求∠B,a,c的值.
17.如图,Rt△ABC中,∠A=90°,AD、AE分别是BC边的中线和高,若cosB=,BC=10.
(1)求AB的长;
(2)求AE的长;
(3)求sin∠ADB的值.
18.【问题背景】如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为
.
【探索延伸】如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
参考答案
一.选择题
1.解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA?cosC=1,
∴AD==;
在Rt△ABD中,BD=CB﹣CD=3,AD=,
∴AB==2,
∴sinB==.
故选:D.
2.解:连接BC,
∵每个小正方形的边长均为1,
∴AB=,BC=,AC=,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
∴sin∠BAC===,
故选:B.
3.解:如图,过点D作DE⊥AB于点E,
∵等腰直角三角形ABC中,∠C=90°,AC=6,
∴AB=6,∠B=45°,且DE⊥AB
∴∠EDB=∠B=45°,
∴DE=BE,
∵tan∠DAB==,
∴AE=5DE,
∵AB=AE+BE=5DE+DE=6DE=6
∴DE=,AE=5
∴AD==2
故选:C.
4.解:如图,过B作BE∥AC交CD于E.
∵AC⊥BC,
∴BE⊥BC,∠CBE=90°,
∴BE∥AC.
∵AB=BD,
∴AC=2BE.
又∵tan∠BCD=,设BE=x,则BC=3x,AC=2x,
∴tanA===.
故选:D.
5.解:∵在△ABC中,∠ACB=90°,sinA=,CD平分∠ACB,
∴∠A=30°,∠ACD=45°,
∵∠BDC=∠A+∠ACD,
∴∠BDC=75°,
故选:D.
6.解:过点(4,2)作直线CD⊥x轴交OA于点C,交x轴于点D,
∵在平面直角坐标系中,直线OA过点(4,2),
∴OD=4,CD=2,
∴tanα=,
故选:A.
7.解:∵tan∠BCE=,
∴∠BCE=30°,
∴∠B=60°,
又∵在Rt△ABD中,AD=3,
∴BD=3,AB=6,
∵BE=2AE,
∴BE=4,AE=2,
在Rt△BEC中,BE=4,∠BCE=30°
∴CE=4,
故选:D.
8.解:如图作AH⊥CB交CB的延长线于H.
∵∠ABD=90°,∠DBC=45°,
∴∠ABH=45°,
∵∠AHB=90°,
∴△ABH是等腰直角三角形,
∴AH=BH,
设AH=BH=a,则AB=a,BD=a,BC=CD=a,CH=a+a,
∵∠AHB=∠DCB=90°,
∴AH∥DC,
∴∠ACD=∠CAH,
∴tan∠ACD=tan∠CAH==+1,
故选:C.
9.解:∵tanB=tanC=tan∠MAN=1,
∴∠B=∠C=∠MAN=45°,
∵∠CAB=90°,
∴AC=AB,
将△BAM绕点A顺时针旋转90°至△ACN′,点B与点C重合,点M落在N′处,连接NN′,
则有AN′=AM,CN′=BM,∠1=∠3,
∵∠MCN=45°,
∴∠1+∠2=45°,
∴∠2+∠3=45°,
∴∠NAN′=∠MAN.
在△MAN与△NAN′中,
,
∴△MAN≌△NCN′(SAS),
∴MN=NN′.
由旋转性质可知,∠ACN′=∠B=45°,
∴∠NCN′=∠ACN′+∠ACB=90°,
∴NN'2=NC2+N'C2,
即x2=n2+m2,
故选:D.
10.解:过点A作AE⊥BC于点E,如图所示:
∵AB=AC=5,
∴BE=BC=×8=4,∠BAE=∠BAC,
∵∠BPC=∠BAC,
∴∠BPC=∠BAE.
在Rt△BAE中,由勾股定理得
AE===3,
∴cos∠BPC=cos∠BAE==.
故选:C.
二.填空题
11.解:过B点作BD⊥AC于点D,
∵cosA=,
∴,
设AD=4x,则AB=5x,
∴,
∵AB=AC,
∴AC=5x,
∴CD=5x﹣4x=x,
∴BC=,
∴,
故答案为:.
12.解:如图,作PD⊥AC于点D,
在Rt△ABC中,∠B=90°,AC=5,BC=3,
∴AB==4,
在Rt△CBP中,CP=,BC=3,
∴BP==,
∴AP=AB﹣BP=,
∵sin∠A==,
即=,
∴PD=,
∴sin∠PCA==×=.
故答案为:.
13.解:过点D作DE⊥AC,与AC的延长线交于点E,
∵AB=AC,
∴∠B=∠ACB,
∵∠DCE=∠ACB,
∴∠DCE=∠B,
∵sinB=,
∴,
不妨设DE=4x,则CD=5x,
∴,
∵CD:AC=1:3,
∴AC=3CD=15x,
∴AE=AC+CE=18x,
∴tan∠CAD=,
故答案为
14.解:当△ABC是锐角三角形时,如图1,
∵BC=6,=2,
∴BD=4,
∵tanB=,
∴=,
∴AD=,
∴S△ABC===8;
当△ABC是钝角三角形时,如图2,
∵BC=6,=2,
∴BD=12,
∵tanB=,
∴=,
∴AD=8,
∴S△ABC===24,
综上,△ABC的面积为8或24,
故答案为8或24.
15.解:过点D作DG⊥BC于点G,
∵AB=AC=13,cos∠ABC=,
∴BE=5,
由勾股定理可知:AE=12,
∵AE⊥BC,
∴BE=EC=5,
∵D是AC的中点,DG∥AE,
∴DG是△AEC的中位线,
∴DG=AE=6,EG=CE=,
∴BG=,
在Rt△BDG中,
tan∠DBC===,
故答案为:
三.解答题
16.解:∵∠C=90°,b=8,∠A的平分线AD=,
∴cos∠CAD==,
∴∠CAD=30°,
∴∠CAB=60°,
∴∠B=30°,
∴c=2b=16,a===8,
即∠B=30°,a=8,c=16.
17.解:(1)在Rt△ABC中,∠A=90°,cosB=,BC=10,
∴AB=BC?cosB=10×=6.
(2)在Rt△ABC中,∠A=90°,BC=10,AB=6,
∴AC===8.
∵AE是BC边的高,
∴AC?AB=BC?AE,即×8×6=×10AE,
∴AE=.
(3)Rt△ABC中,AD是BC边的中线,BC=10,
∴AD=BC=5.
在Rt△AED中,∠AED=90°,AD=5,AE=,
∴sin∠ADB===.
18.解:(1)如图1,
∵BE∥CD,
∴∠ABE=∠CPB,
∴tan∠ABE=tan∠CPB,
∵∠AEB=90°,
∴tan∠CPB=tan∠ABE===3,
故答案为3.
(2)如图2,连接CE,DE,作DM⊥CE于M.
∵BC∥AE,BC=AE,
∴四边形ABCE是平行四边形,
∴CE∥AB,
∴∠APD=∠ECD.
∵△ECD的面积=3×4﹣×1×4﹣×2×3﹣×1×3=,
∴CE?DM=,
∵CE=,
∴DM=,
∴sin∠APD=sin∠ECD==÷=.
同步练习
一.选择题
1.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A.
B.
C.
D.
2.如图,A、B、C分别是小正方形的三个顶点,且每个小正方形的边长均为1,则sin∠BAC的值为( )
A.
B.
C.1
D.
3.如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是BC上一点,若tan∠DAB=,则AD的长为( )
A.2
B.
C.2
D.8
4.如图,延长Rt△ABC的斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA的值是( )
A.1
B.
C.9
D.
5.如图,在△ABC中,∠ACB=90°,sinA=,CD平分∠ACB,则∠BDC的度数是( )
A.45°
B.60°
C.70°
D.75°
6.如图,在平面直角坐标系中,直线OA过点(4,2),则tanα的值是( )
A.
B.
C.
D.2
7.如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=3,tan∠BCE=,那么CE等于( )
A.2
B.3﹣2
C.5
D.4
8.将一副三角板如图摆放在一起,组成四边形ABCD,连接AC,则tan∠ACD的值等于( )
A.2
B.2+
C.1+
D.2
9.如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )
A.m=n
B.x=m+n
C.x>m+n
D.x2=m2+n2
10.如图,△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,则cos∠BPC=( )
A.
B.
C.
D.
二.填空题
11.在△ABC中,AB=AC,若cosA=,则=
.
12.在Rt△ABC中,∠B=90°,AC=5,BC=3,P为线段AB上一点,且CP=,则sin∠PCA的值为
.
13.如图,在△ABC中,AB=AC,sinB=,延长BC至点D,使CD:AC=1:3,则tan∠CAD=
.
14.已知在△ABC中,tanB=,BC=6,过点A作BC边上的高,垂足为D,且=2,则△ABC的面积为
.
15.如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=,AB=13.则tan∠DBC的值为
.
三.解答题
16.如图,在Rt△ABC中,设a,b,c分别为∠A,∠B,∠C的对边,∠C=90°,b=8,∠A的平分线AD=,求∠B,a,c的值.
17.如图,Rt△ABC中,∠A=90°,AD、AE分别是BC边的中线和高,若cosB=,BC=10.
(1)求AB的长;
(2)求AE的长;
(3)求sin∠ADB的值.
18.【问题背景】如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为
.
【探索延伸】如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
参考答案
一.选择题
1.解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA?cosC=1,
∴AD==;
在Rt△ABD中,BD=CB﹣CD=3,AD=,
∴AB==2,
∴sinB==.
故选:D.
2.解:连接BC,
∵每个小正方形的边长均为1,
∴AB=,BC=,AC=,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
∴sin∠BAC===,
故选:B.
3.解:如图,过点D作DE⊥AB于点E,
∵等腰直角三角形ABC中,∠C=90°,AC=6,
∴AB=6,∠B=45°,且DE⊥AB
∴∠EDB=∠B=45°,
∴DE=BE,
∵tan∠DAB==,
∴AE=5DE,
∵AB=AE+BE=5DE+DE=6DE=6
∴DE=,AE=5
∴AD==2
故选:C.
4.解:如图,过B作BE∥AC交CD于E.
∵AC⊥BC,
∴BE⊥BC,∠CBE=90°,
∴BE∥AC.
∵AB=BD,
∴AC=2BE.
又∵tan∠BCD=,设BE=x,则BC=3x,AC=2x,
∴tanA===.
故选:D.
5.解:∵在△ABC中,∠ACB=90°,sinA=,CD平分∠ACB,
∴∠A=30°,∠ACD=45°,
∵∠BDC=∠A+∠ACD,
∴∠BDC=75°,
故选:D.
6.解:过点(4,2)作直线CD⊥x轴交OA于点C,交x轴于点D,
∵在平面直角坐标系中,直线OA过点(4,2),
∴OD=4,CD=2,
∴tanα=,
故选:A.
7.解:∵tan∠BCE=,
∴∠BCE=30°,
∴∠B=60°,
又∵在Rt△ABD中,AD=3,
∴BD=3,AB=6,
∵BE=2AE,
∴BE=4,AE=2,
在Rt△BEC中,BE=4,∠BCE=30°
∴CE=4,
故选:D.
8.解:如图作AH⊥CB交CB的延长线于H.
∵∠ABD=90°,∠DBC=45°,
∴∠ABH=45°,
∵∠AHB=90°,
∴△ABH是等腰直角三角形,
∴AH=BH,
设AH=BH=a,则AB=a,BD=a,BC=CD=a,CH=a+a,
∵∠AHB=∠DCB=90°,
∴AH∥DC,
∴∠ACD=∠CAH,
∴tan∠ACD=tan∠CAH==+1,
故选:C.
9.解:∵tanB=tanC=tan∠MAN=1,
∴∠B=∠C=∠MAN=45°,
∵∠CAB=90°,
∴AC=AB,
将△BAM绕点A顺时针旋转90°至△ACN′,点B与点C重合,点M落在N′处,连接NN′,
则有AN′=AM,CN′=BM,∠1=∠3,
∵∠MCN=45°,
∴∠1+∠2=45°,
∴∠2+∠3=45°,
∴∠NAN′=∠MAN.
在△MAN与△NAN′中,
,
∴△MAN≌△NCN′(SAS),
∴MN=NN′.
由旋转性质可知,∠ACN′=∠B=45°,
∴∠NCN′=∠ACN′+∠ACB=90°,
∴NN'2=NC2+N'C2,
即x2=n2+m2,
故选:D.
10.解:过点A作AE⊥BC于点E,如图所示:
∵AB=AC=5,
∴BE=BC=×8=4,∠BAE=∠BAC,
∵∠BPC=∠BAC,
∴∠BPC=∠BAE.
在Rt△BAE中,由勾股定理得
AE===3,
∴cos∠BPC=cos∠BAE==.
故选:C.
二.填空题
11.解:过B点作BD⊥AC于点D,
∵cosA=,
∴,
设AD=4x,则AB=5x,
∴,
∵AB=AC,
∴AC=5x,
∴CD=5x﹣4x=x,
∴BC=,
∴,
故答案为:.
12.解:如图,作PD⊥AC于点D,
在Rt△ABC中,∠B=90°,AC=5,BC=3,
∴AB==4,
在Rt△CBP中,CP=,BC=3,
∴BP==,
∴AP=AB﹣BP=,
∵sin∠A==,
即=,
∴PD=,
∴sin∠PCA==×=.
故答案为:.
13.解:过点D作DE⊥AC,与AC的延长线交于点E,
∵AB=AC,
∴∠B=∠ACB,
∵∠DCE=∠ACB,
∴∠DCE=∠B,
∵sinB=,
∴,
不妨设DE=4x,则CD=5x,
∴,
∵CD:AC=1:3,
∴AC=3CD=15x,
∴AE=AC+CE=18x,
∴tan∠CAD=,
故答案为
14.解:当△ABC是锐角三角形时,如图1,
∵BC=6,=2,
∴BD=4,
∵tanB=,
∴=,
∴AD=,
∴S△ABC===8;
当△ABC是钝角三角形时,如图2,
∵BC=6,=2,
∴BD=12,
∵tanB=,
∴=,
∴AD=8,
∴S△ABC===24,
综上,△ABC的面积为8或24,
故答案为8或24.
15.解:过点D作DG⊥BC于点G,
∵AB=AC=13,cos∠ABC=,
∴BE=5,
由勾股定理可知:AE=12,
∵AE⊥BC,
∴BE=EC=5,
∵D是AC的中点,DG∥AE,
∴DG是△AEC的中位线,
∴DG=AE=6,EG=CE=,
∴BG=,
在Rt△BDG中,
tan∠DBC===,
故答案为:
三.解答题
16.解:∵∠C=90°,b=8,∠A的平分线AD=,
∴cos∠CAD==,
∴∠CAD=30°,
∴∠CAB=60°,
∴∠B=30°,
∴c=2b=16,a===8,
即∠B=30°,a=8,c=16.
17.解:(1)在Rt△ABC中,∠A=90°,cosB=,BC=10,
∴AB=BC?cosB=10×=6.
(2)在Rt△ABC中,∠A=90°,BC=10,AB=6,
∴AC===8.
∵AE是BC边的高,
∴AC?AB=BC?AE,即×8×6=×10AE,
∴AE=.
(3)Rt△ABC中,AD是BC边的中线,BC=10,
∴AD=BC=5.
在Rt△AED中,∠AED=90°,AD=5,AE=,
∴sin∠ADB===.
18.解:(1)如图1,
∵BE∥CD,
∴∠ABE=∠CPB,
∴tan∠ABE=tan∠CPB,
∵∠AEB=90°,
∴tan∠CPB=tan∠ABE===3,
故答案为3.
(2)如图2,连接CE,DE,作DM⊥CE于M.
∵BC∥AE,BC=AE,
∴四边形ABCE是平行四边形,
∴CE∥AB,
∴∠APD=∠ECD.
∵△ECD的面积=3×4﹣×1×4﹣×2×3﹣×1×3=,
∴CE?DM=,
∵CE=,
∴DM=,
∴sin∠APD=sin∠ECD==÷=.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
