苏科版九年级下册数学学案:5.2二次函数y=a(x-h)2+k 的图象(二)(表格式 无答案)
文档属性
| 名称 | 苏科版九年级下册数学学案:5.2二次函数y=a(x-h)2+k 的图象(二)(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 126.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览

文档简介
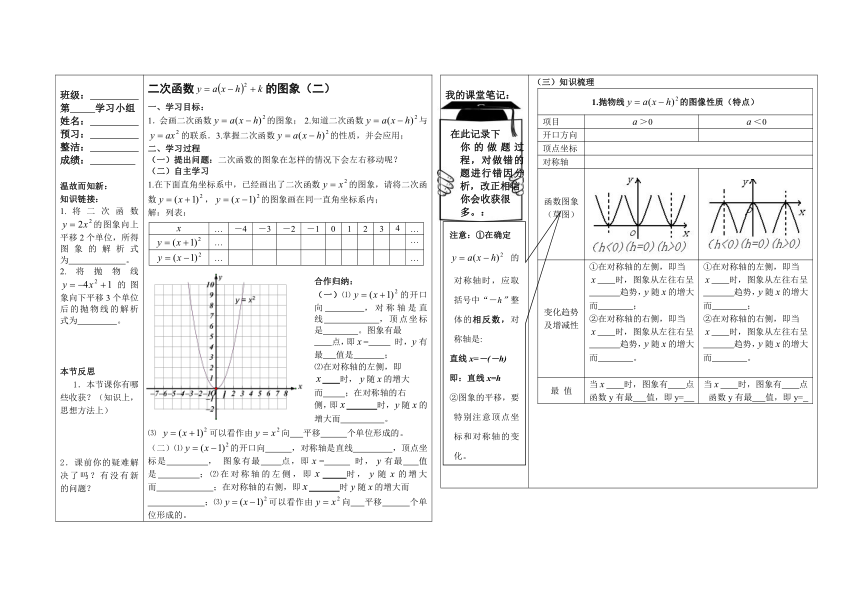
班级:
第
学习小组
姓名:
预习:
整洁:
成绩:
温故而知新:
知识链接:
1.将二次函数的图象向上平移2个单位,所得图象的解析式为
。
2.将抛物线的图象向下平移3个单位后的抛物线的解析式为
。
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
我的课堂笔记:
在此记录下
你的做题过程,对做错的题进行错因分析,改正相信
你会收获很
多。:
二次函数的图象(二)
一、学习目标:
1.会画二次函数的图象;
2.知道二次函数与的联系.3.掌握二次函数的性质,并会应用;
二、学习过程
(一)提出问题:二次函数的图象在怎样的情况下会左右移动呢?
(二)自主学习
1.在下面直角坐标系中,已经画出了二次函数的图象,请将二次函数,的图象画在同一直角坐标系内;
解:列表:
…-4-3-2-101234……………
合作归纳:
(一)⑴的开口向
,对称轴是直线
,顶点坐标是
。图象有最
点,即=
时,有最
值是
;
⑵在对称轴的左侧,即
时,随的增大
而
;在对称轴的右
侧,即
时,随的增大而
。
⑶
可以看作由向
平移
个单位形成的。
⑴的开口向
,对称轴是直线
,顶点坐标是
,
图象有最
点,即=
时,有最
值是
;⑵在对称轴的左侧,即
时,随的增大而
;在对称轴的右侧,即
时随的增大而
;⑶可以看作由向
平移
个单位形成的。
(三)知识梳理
1.抛物线的图像性质(特点)项目>0<0开口方向顶点坐标对称轴
函数图象
(草图)
变化趋势及增减性①在对称轴的左侧,即当
时,图象从左往右呈
趋势,随的增大而
;
②在对称轴的右侧,即当
时,图象从左往右呈
趋势,随的增大而
。
①在对称轴的左侧,即当
时,图象从左往右呈
趋势,随的增大而
;
②在对称轴的右侧,即当
时,图象从左往右呈
趋势,随的增大而
。
最
值当
时,图象有
点函数y有最
值,即y=
当
时,图象有
点函数y有最
值,即y=
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
2.抛物线与形状
,位置
,
是由
平移得到的。(填上下或左右)
二次函数图象的左右平移规律:由h的符号确定:
左
右。
“―h”整体的符号“左
+
右
―”
3.
的正负决定开口的
;决定开口的
,即不变,则抛物线的形状
。因为平移没有改变抛物线的开口方向和形状,所以平移前后的两条抛物线值
。
(四)课堂训练
1.抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当
时,随的增大而减小;当
时,随的增大而增大。
2.
抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当
时,随的增大而减小;当
时,随的增大而增大。
3.
抛物线的开口_____;顶点坐标为_______;对称轴是_____;
4.抛物线向右平移4个单位后,得到的抛物线的表达式为______________.
(五)课后巩固
1.
抛物线向左平移3个单位后,得到的抛物线的表达式为______________.
2.将抛物线向右平移1个单位后,得到的抛物线解析式为__________.
3.抛物线与y轴的交点坐标是_______,与x轴的交点坐标为________.
4.
写出一个顶点是(5,0),形状、开口方向与抛物线都相同的二次函数解析式?
5.写出抛物线的特点?
第
学习小组
姓名:
预习:
整洁:
成绩:
温故而知新:
知识链接:
1.将二次函数的图象向上平移2个单位,所得图象的解析式为
。
2.将抛物线的图象向下平移3个单位后的抛物线的解析式为
。
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
我的课堂笔记:
在此记录下
你的做题过程,对做错的题进行错因分析,改正相信
你会收获很
多。:
二次函数的图象(二)
一、学习目标:
1.会画二次函数的图象;
2.知道二次函数与的联系.3.掌握二次函数的性质,并会应用;
二、学习过程
(一)提出问题:二次函数的图象在怎样的情况下会左右移动呢?
(二)自主学习
1.在下面直角坐标系中,已经画出了二次函数的图象,请将二次函数,的图象画在同一直角坐标系内;
解:列表:
…-4-3-2-101234……………
合作归纳:
(一)⑴的开口向
,对称轴是直线
,顶点坐标是
。图象有最
点,即=
时,有最
值是
;
⑵在对称轴的左侧,即
时,随的增大
而
;在对称轴的右
侧,即
时,随的增大而
。
⑶
可以看作由向
平移
个单位形成的。
⑴的开口向
,对称轴是直线
,顶点坐标是
,
图象有最
点,即=
时,有最
值是
;⑵在对称轴的左侧,即
时,随的增大而
;在对称轴的右侧,即
时随的增大而
;⑶可以看作由向
平移
个单位形成的。
(三)知识梳理
1.抛物线的图像性质(特点)项目>0<0开口方向顶点坐标对称轴
函数图象
(草图)
变化趋势及增减性①在对称轴的左侧,即当
时,图象从左往右呈
趋势,随的增大而
;
②在对称轴的右侧,即当
时,图象从左往右呈
趋势,随的增大而
。
①在对称轴的左侧,即当
时,图象从左往右呈
趋势,随的增大而
;
②在对称轴的右侧,即当
时,图象从左往右呈
趋势,随的增大而
。
最
值当
时,图象有
点函数y有最
值,即y=
当
时,图象有
点函数y有最
值,即y=
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
2.抛物线与形状
,位置
,
是由
平移得到的。(填上下或左右)
二次函数图象的左右平移规律:由h的符号确定:
左
右。
“―h”整体的符号“左
+
右
―”
3.
的正负决定开口的
;决定开口的
,即不变,则抛物线的形状
。因为平移没有改变抛物线的开口方向和形状,所以平移前后的两条抛物线值
。
(四)课堂训练
1.抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当
时,随的增大而减小;当
时,随的增大而增大。
2.
抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当
时,随的增大而减小;当
时,随的增大而增大。
3.
抛物线的开口_____;顶点坐标为_______;对称轴是_____;
4.抛物线向右平移4个单位后,得到的抛物线的表达式为______________.
(五)课后巩固
1.
抛物线向左平移3个单位后,得到的抛物线的表达式为______________.
2.将抛物线向右平移1个单位后,得到的抛物线解析式为__________.
3.抛物线与y轴的交点坐标是_______,与x轴的交点坐标为________.
4.
写出一个顶点是(5,0),形状、开口方向与抛物线都相同的二次函数解析式?
5.写出抛物线的特点?
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
