华东师大版九年级数学下册 27.2 与圆有关的位置关系 同步测试题(Word版 有答案)
文档属性
| 名称 | 华东师大版九年级数学下册 27.2 与圆有关的位置关系 同步测试题(Word版 有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 270.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览



文档简介
106172001074420012319000027.2 与圆有关的位置关系 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
?1. 已知点A在半径为3的圆上,则点A与圆心O的距离等于(? ? ? ? )
A.2 B.3 C.4 D.5
?
2. 已知∠AOB=60?,半径为23的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
A.2 B.2或6 C.4或6 D.1或5
?
3. 圆外切等腰梯形的一腰长是8,则这个等腰梯形的上底与下底长的和为( )
A.4 B.8 C.12 D.16
?
4. 两圆外离,作它们的两条内公切线,四个切点构成的四边形是( )
A.矩形 B.等腰梯形
C.矩形或等腰梯形 D.菱形
?5. 下列直线中,可以判定为圆的切线的是( )
A.与圆仅有一个公共点的直线 B.垂直于圆的半径的直线
C.与圆心的距离等于直径的直线 D.过圆的半径外端的直线
?6. 下列关于三角形的内心和外心的说法中,正确的说法为( )
①三角形的内心是三角形内切圆的圆心;②三角形的内心是三个角平分线的交点;
③三角形的外心到三边的距离相等;④三角形的外心是三边中垂线的交点.
A.①②③④ B.①②③ C.①②④ D.②③④
?
7. 如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是AB上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
?
8. 已知⊙O的半径为5,直线l和点O的距离为d?cm,若直线l与⊙O有公共点,则( )
A.d>5 B.d=5 C.d<5 D.0≤d≤5
?
9. 已知,Rt△ABC中,∠C=90?,AC=3cm,BC=4cm,则△ABC的外接圆半径和△ABC的外心与内心之间的距离分别为( )
A.5和5 B.52和52 C.52和5 D.52和12
?
10. AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC C.CD=DB D.AC?//?OD
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 ) ?
11. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是________.
?
12. ⊙O是Rt△ABC的内切圆,切点为D、E、F,若AF、BE的长分别是3和10,则内切圆的半径是________.
?
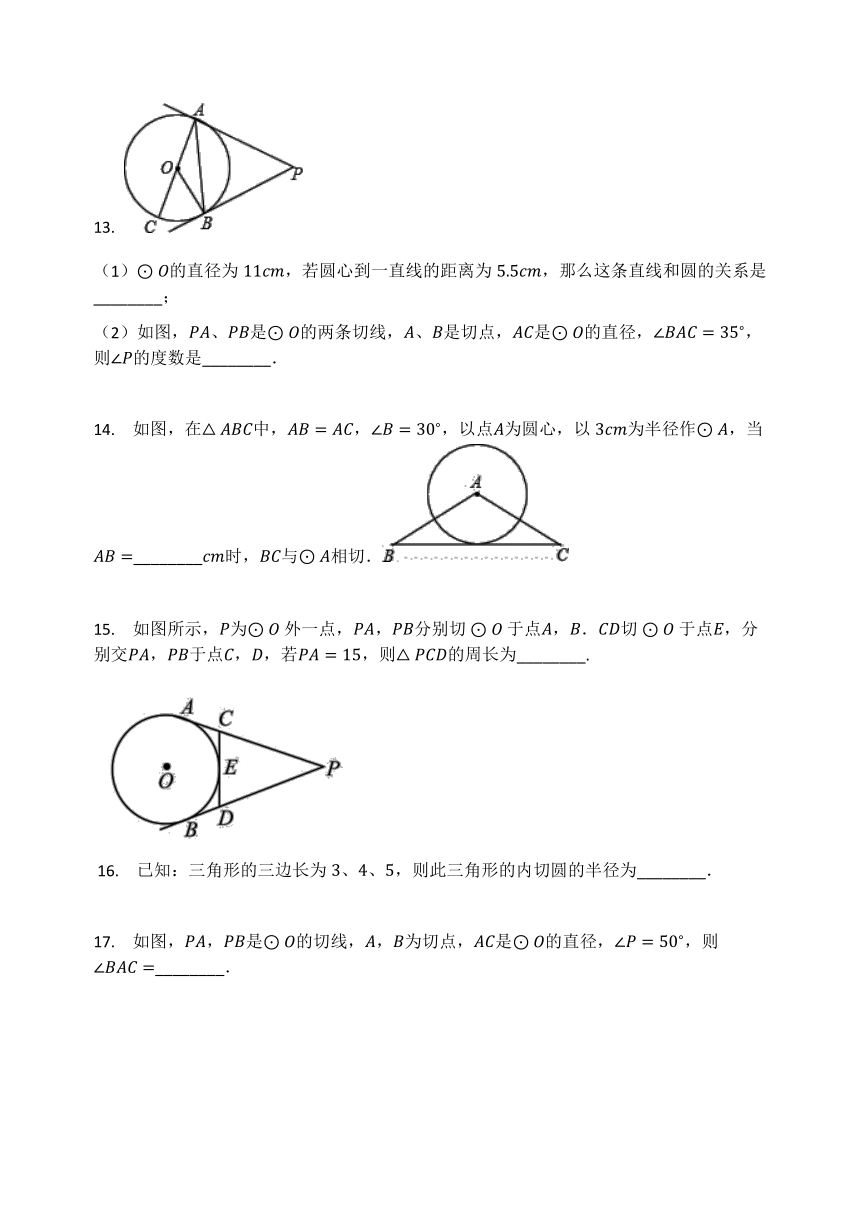
13.
(1)⊙O的直径为11cm,若圆心到一直线的距离为5.5cm,那么这条直线和圆的关系是________;
(2)如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35?,则∠P的度数是________.
?
14. 如图,在△ABC中,AB=AC,∠B=30?,以点A为圆心,以3cm为半径作⊙A,当AB=________cm时,BC与⊙A相切.
?
15. 如图所示,P为⊙O?外一点,PA,PB分别切?⊙O?于点A,B.CD切?⊙O?于点E,分别交PA,PB于点C,D,若PA=15,则△PCD的周长为________.
?16. 已知:三角形的三边长为3、4、5,则此三角形的内切圆的半径为________.
?
17. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=50?,则∠BAC=________.
?
18. 如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为________cm.
三、 解答题 (本题共计 6 小题 ,共计60分 ) ?
19. 已知⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A、B、C三点,AD=6,BD=8,CD=53,问:A、B、C三点与⊙O的位置关系.
?
20. 如图,△ABC内接于圆O,若圆的半径是2,AB=3,求sinC.
?
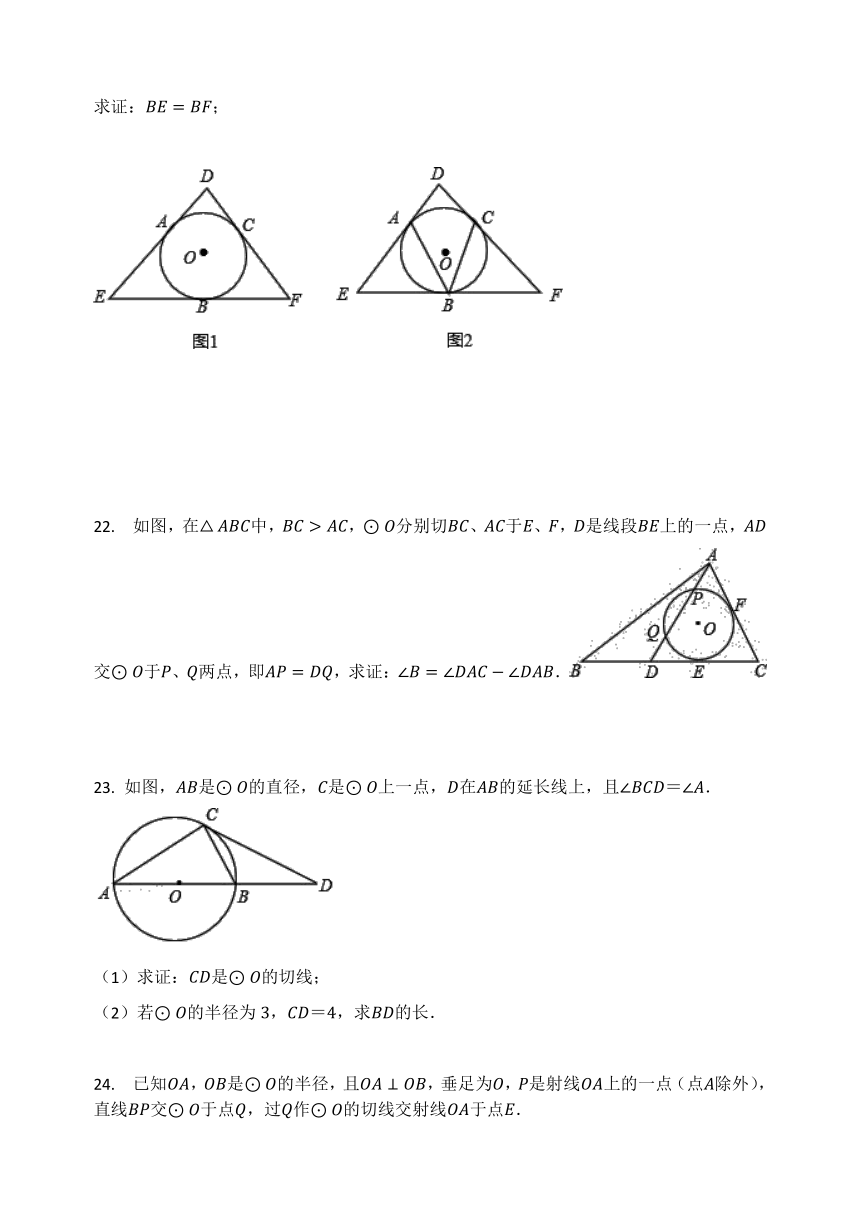
21. 已知⊙O为△DEF的内切圆,切点分别为A、B、C,AB=BC
求证:BE=BF;
?
22. 如图,在△ABC中,BC>AC,⊙O分别切BC、AC于E、F,D是线段BE上的一点,AD交⊙O于P、Q两点,即AP=DQ,求证:∠B=∠DAC-∠DAB.
?
23. 如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
?
24. 已知OA,OB是⊙O的半径,且OA⊥OB,垂足为O,P是射线OA上的一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交射线OA于点E.
(I)如图①,点P在线段OA上,若∠OBQ=15?,求∠AQE的大小;
(Ⅱ)如图②,点P在OA的延长线上,若∠OBQ=65?,求∠AQE的大小.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ 点A在半径为3的圆上,
∴ 点A与圆心的距离d=3.
故选B.
2.
【答案】
B
【解答】
当将⊙M水平向左平移,当点M运动到M'位置时,如图
作MC⊥OA于C点,M'H⊥OA于H,M'Q⊥MC于Q,连结M'E,
∵ ⊙M与边OB、OA相切,
∴ MM'?//?OB,MC=23,
∵ M'H⊥OA,
∴ EH=FH=12EF=12×6=3,
在Rt△EHM'中,EM'=23,
∴ HM'=EM?'2-EH2=3,
∵ M'Q⊥MC,
∴ 四边形M'QCH为矩形,
∴ CQ=M'H=3,
∴ MQ=23-3=3,
∵ ∠QMM'=∠AOB=60?,
∴ ∠QM'M=30?,
∴ M'Q=MQ3=1,
∴ MM'=2;
当将⊙M水平向左平移,当点M运动到M″位置时,如图2,
作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,
易得MC=23,M'H=3,
∵ ∠MDC=∠M″DH=∠AOB=60?,
∴ ∠HM″D=30?,∠CMD=30?,
在Rt△HM″D中,M″D=3,则DH=M″D3=1,
∴ M″D=2DH=2,
在Rt△CDM中,CM=23,则DC=MC3=2,
∴ DM=2DC=4,
∴ MM″=2+4=6,
综上所述,当⊙M平移的距离为2或6.
3.
【答案】
D
【解答】
解:∵ 圆外切等腰梯形的一腰长是8,
∴ 梯形对边和为:8+8=16,
则这个等腰梯形的上底与下底长的和为16.
故选:D.
4.
【答案】
C
【解答】
解:∵ TA,TC是圆O的切线.
∴ TA=TC,
∴ ∠TAC=∠TCA,
同理,∠TDB=∠TBD,
又∵ ∠ATC=∠BTD,
∴ ∠TAC=∠TBD,
∴ AC?//?BD,
当TA=TB时,TA=TC=TB=TD,则四边形ACBD是矩形.
当TA≠TB时,AB=CD,则四边形ACBD是等腰梯形,
故选C.
5.
【答案】
A
【解答】
解:A、根据圆的切线的定义,可知与圆仅有一个公共点的直线是切线,故选项正确;
B、垂直于圆的半径的直线,可能与圆相交或相离,故选项错误;
C、与圆心的距离等于直径的直线与圆相离,故选项错误;
D、过圆的半径外端的直线与圆相交或相切,故选项错误.
故选A.
6.
【答案】
C
【解答】
解:①三角形的内心是三角形内切圆的圆心;是三角形的内心的定义,故正确;
②∵ 三角形内切圆与各边都相切,
∴ 由切线长定理可得:三角形的内心是三个角平分线的交点;故正确;
③∵ 三角形的外心是三角形外接圆的圆心,
∴ 三角形的外心到三个顶点的距离相等;故错误;
④三角形的外心是三边中垂线的交点,正确.
∴ 正确的说法为:①②④.
故选C.
7.
【答案】
B
【解答】
解:∵ PA,PB分别和⊙O切于A,B两点,
∴ PA=PB,
∵ DE是⊙O的切线,
∴ DA=DC,EB=EC,
∵ △PDE的周长为12,
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,
∴ PA=6.
故选B.
8.
【答案】
D
【解答】
解:∵ ⊙O与直线有公共点,
∴ 直线L与圆相切或相交,
∴ 点O到直线L的距离小于或等于圆的半径,
即d≤5,
∵ d≥0,
∴ 0≤d≤5.
故选D.
9.
【答案】
B
【解答】
(2)连接ID,IE,IF,
∵ ⊙I是△ABC的内切圆,
∴ ID⊥BC,IE⊥AC,IF⊥AB,
∴ ∠CDI=∠CEI=∠C=90?,
又∵ DI=EI,
∴ 四边形CDIE是正方形.
∴ CD=CE=DI=IE(1)∵ AC=3cm,BC=4cm,由(1)知AB=5cm,
∴ △ABC的内切圆半径长r=a+b-c2,
=3+4-52
=1cm.
即DI=EI=FI=1cm(2)∴ CD=1cm.
∵ BC=4cm,
∴ BD=3cm.
∵ ⊙I是△ABC的内切圆,
∴ BD=BF=3cm.
∵ BO=52cm,
∴ OF=12cm.
在Rt△IFO中,IO=52cm(勾股定理).
∴ △ABC的外心与内心之间的距离为52cm.
故选:B.
10.
【答案】
A
【解答】
当AB=AC时,如图:连接AD,
∵ AB是⊙O的直径,
∴ AD⊥BC,
∴ CD=BD,
∵ AO=BO,
∴ OD是△ABC的中位线,
∴ OD?//?AC,
∵ DE⊥AC,
∴ DE⊥OD,
∴ DE是⊙O的切线.
所以B正确.
当CD=BD时,AO=BO,∴ OD是△ABC的中位线,
∴ OD?//?AC
∵ DE⊥AC
∴ DE⊥OD
∴ DE是⊙O的切线.
所以C正确.
当AC?//?OD时,∵ DE⊥AC,∴ DE⊥OD.
∴ DE是⊙O的切线.
所以D正确.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
相交
【解答】
解:∵ 矩形ABCD中,BC=2.8,
∴ 圆心到CD的距离为2.8.
∵ AB为直径,AB=6,
∴ 半径是3.
∵ 2.8<3,
∴ 直线DC与⊙O相交.
故答案为:相交.
12.
【答案】
2
【解答】
解:连接OE、OD,设⊙O的半径为R,
∵ ⊙O是直角三角形ABC的内切圆,
∴ BE=BF=10,AF=AD=3,∠OEC=∠C=∠ODC=90?,OE=OD,
∴ 四边形ECDO是正方形,
∴ OE=CE=CD=OD=R,
由勾股定理得:(R+10)2+(R+3)2=(10+3)2,
解得:R=2,
故答案为:2.
13.
【答案】
相切,70?.
【解答】
解:(1)∵ ⊙O的直径为11cm,圆心O到一条直线的距离为5.5cm,
∴ 直线与圆相切;
(2)根据切线的性质定理得∠PAC=90?,
∴ ∠PAB=90?-∠BAC=90?-35?=55?.
根据切线长定理得PA=PB,
所以∠PBA=∠PAB=55?,
所以∠P=70?.
14.
【答案】
6
【解答】
解:如图,过点A作AD⊥BC于点D.
∵ AB=AC,∠B=30?,
∴ AD=12AB,即AB=2AD.
又∵ BC与⊙A相切,
∴ AD就是圆A的半径,
∴ AD=3cm,
则AB=2AD=6cm.
故答案是:6.
15.
【答案】
30
【解答】
解:∵ PA,PB分别切⊙O?于A,B,
∴ PA=PB=15.
同理可知:EC=CA,DE=DB,
∴ △PDC的周长=PC+CE+DE+DP
=PC+AC+PD+DB
=PA+PB
=2PA
=30.
故答案为:30.
16.
【答案】
1
【解答】
解:如图所示:△ABC中,AC=3,BC=4,AB=5,
∵ 32+42=52,即AC2+BC2=AB2,
∴ △ABC是直角三角形,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵ CD=CE,BE=BF,AF=AD,
∵ OD⊥AC,OE⊥BC,
∴ 四边形ODCE是正方形,即CD=CE=R,
∴ AC-CD=AB-BF,即3-R=5-BF①
BC-CE=AB-AF,即4-R=BF②,
①②联立得,R=1.
故答案为:1.
17.
【答案】
25?
【解答】
解:连接OB,
∵ PA,PB是⊙O的切线,A,B为切点,
∴ ∠PAO=∠PBO=90?,
∴ ∠AOB=360?-∠P-∠PAO-∠PBO=130?,
∵ OA=OB,
∴ ∠BAC=25?.
故答案为:25?.
18.
【答案】
20
【解答】
解:∵ PA,PB是圆的切线.
∴ PA=PB
同理,AE=EC,FC=FB.
三角形PEF的周长=PE+EF+PF=PE+PF+CF+EC=PE+AE+PF+FB=PA+PB=2PA=20cm.
故答案是20.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
19.
【答案】
解:OA=OD2+AD2=62,
BO=OD2+BD2=10,
CO=OD2+CD2=111,
∵ ⊙O的半径r=10,
∴ 点A在⊙O内,点B在⊙O上,点C在⊙O外.
【解答】
解:OA=OD2+AD2=62,
BO=OD2+BD2=10,
CO=OD2+CD2=111,
∵ ⊙O的半径r=10,
∴ 点A在⊙O内,点B在⊙O上,点C在⊙O外.
20.
【答案】
解:
作直径AD,连接BD,
∵ ∠ACB和∠ADB都对弧AB,
∴ ∠ACB=∠ADB,
∵ 圆的半径是2,
∴ AD=2+2=4,
∵ AD为直径,
∴ ∠ABD=90?,
∴ sinC=sinD=ABAD=34.
【解答】
解:
作直径AD,连接BD,
∵ ∠ACB和∠ADB都对弧AB,
∴ ∠ACB=∠ADB,
∵ 圆的半径是2,
∴ AD=2+2=4,
∵ AD为直径,
∴ ∠ABD=90?,
∴ sinC=sinD=ABAD=34.
21.
【答案】
解(1)如图2,连接AC,
∵ AB=BC,
∴ AB=BC,∠EAB=∠EBA=∠FCB=∠FBC,
∴ △AEB?△CFB,
∴ BE=BF;
(2)如图2,连接AC,作DG⊥AC于G,AH⊥DF于H,
∵ DE、DF是⊙O的切线,切点分别为A,C,
∴ ∠ABC=∠DAC=∠DCA,
∴ AD=DC,
∴ AG=CG=12AC,
∴ tan∠DAG=tan∠ABC=DGAG=43,
设DG=4k,则AG=3k,
∴ AC=2AG=6k,AD=CD=5k,12×AC×DG=12×CD×AH,
∴ AH=245k,
∴ sin∠EDF=AHAD=2425.
【解答】
解(1)如图2,连接AC,
∵ AB=BC,
∴ AB=BC,∠EAB=∠EBA=∠FCB=∠FBC,
∴ △AEB?△CFB,
∴ BE=BF;
(2)如图2,连接AC,作DG⊥AC于G,AH⊥DF于H,
∵ DE、DF是⊙O的切线,切点分别为A,C,
∴ ∠ABC=∠DAC=∠DCA,
∴ AD=DC,
∴ AG=CG=12AC,
∴ tan∠DAG=tan∠ABC=DGAG=43,
设DG=4k,则AG=3k,
∴ AC=2AG=6k,AD=CD=5k,12×AC×DG=12×CD×AH,
∴ AH=245k,
∴ sin∠EDF=AHAD=2425.
22.
【答案】
证明:过点O作OH⊥AD于点H,连接OA,OD,OE,OF,
∴ PH=QH,
∵ AP=DQ,
∴ AH=DH,
∴ OA=OD,
∵ ⊙O分别切BC、AC于E、F,
∴ CF=CE,OE⊥BC,OF⊥AC,
即∠AFO=∠DEO=90?,
在Rt△AOF和Rt△DOE中,
OA=ODOF=OE,
∴ Rt△AOF?Rt△DOE(HL),
∴ AF=DE,
∴ AC=DC,
∴ ∠ADC=∠DAC,
∴ ∠B=∠ADC-∠DAB=∠DAC-∠DAB.
【解答】
证明:过点O作OH⊥AD于点H,连接OA,OD,OE,OF,
∴ PH=QH,
∵ AP=DQ,
∴ AH=DH,
∴ OA=OD,
∵ ⊙O分别切BC、AC于E、F,
∴ CF=CE,OE⊥BC,OF⊥AC,
即∠AFO=∠DEO=90?,
在Rt△AOF和Rt△DOE中,
OA=ODOF=OE,
∴ Rt△AOF?Rt△DOE(HL),
∴ AF=DE,
∴ AC=DC,
∴ ∠ADC=∠DAC,
∴ ∠B=∠ADC-∠DAB=∠DAC-∠DAB.
23.
【答案】
证明:连接OC.
∵ AB是⊙O的直径,C是⊙O上一点,
∴ ∠ACB=90?,即∠ACO+∠OCB=90?.
∵ OA=OC,∠BCD=∠A,
∴ ∠ACO=∠A=∠BCD,
∴ ∠BCD+∠OCB=90?,即∠OCD=90?,
∴ CD是⊙O的切线.
在Rt△OCD中,∠OCD=90?,OC=3,CD=4,
∴ OD=OC2+CD2=5,
∴ BD=OD-OB=5-3=2.
【解答】
证明:连接OC.
∵ AB是⊙O的直径,C是⊙O上一点,
∴ ∠ACB=90?,即∠ACO+∠OCB=90?.
∵ OA=OC,∠BCD=∠A,
∴ ∠ACO=∠A=∠BCD,
∴ ∠BCD+∠OCB=90?,即∠OCD=90?,
∴ CD是⊙O的切线.
在Rt△OCD中,∠OCD=90?,OC=3,CD=4,
∴ OD=OC2+CD2=5,
∴ BD=OD-OB=5-3=2.
24.
【答案】
(I)如图①中,连接OQ.
∵ EQ是切线,
∴ OQ⊥EQ,
∴ ∠OQE=90?,
∵ OA⊥OB,
∴ ∠AOB=90?,
∴ ∠AQB=12∠AOB=45?,
∵ OB=OQ,
∴ ∠OBQ=∠OQB=15?,
∴ ∠AQE=90?-15?-45?=30?.
(Ⅱ)如图②中,连接OQ.
∵ OB=OQ,
∴ ∠B=∠OQB=65?,
∴ ∠BOQ=50?,
∵ ∠AOB=90?,
∴ ∠AOQ=40?,
∵ OQ=OA,
∴ ∠OQA=∠OAQ=70?,
∵ EQ是切线,
∴ ∠OQE=90?,
∴ ∠AQE=90?-70?=20?.
【解答】
(I)如图①中,连接OQ.
∵ EQ是切线,
∴ OQ⊥EQ,
∴ ∠OQE=90?,
∵ OA⊥OB,
∴ ∠AOB=90?,
∴ ∠AQB=12∠AOB=45?,
∵ OB=OQ,
∴ ∠OBQ=∠OQB=15?,
∴ ∠AQE=90?-15?-45?=30?.
(Ⅱ)如图②中,连接OQ.
∵ OB=OQ,
∴ ∠B=∠OQB=65?,
∴ ∠BOQ=50?,
∵ ∠AOB=90?,
∴ ∠AOQ=40?,
∵ OQ=OA,
∴ ∠OQA=∠OAQ=70?,
∵ EQ是切线,
∴ ∠OQE=90?,
∴ ∠AQE=90?-70?=20?.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
?1. 已知点A在半径为3的圆上,则点A与圆心O的距离等于(? ? ? ? )
A.2 B.3 C.4 D.5
?
2. 已知∠AOB=60?,半径为23的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
A.2 B.2或6 C.4或6 D.1或5
?
3. 圆外切等腰梯形的一腰长是8,则这个等腰梯形的上底与下底长的和为( )
A.4 B.8 C.12 D.16
?
4. 两圆外离,作它们的两条内公切线,四个切点构成的四边形是( )
A.矩形 B.等腰梯形
C.矩形或等腰梯形 D.菱形
?5. 下列直线中,可以判定为圆的切线的是( )
A.与圆仅有一个公共点的直线 B.垂直于圆的半径的直线
C.与圆心的距离等于直径的直线 D.过圆的半径外端的直线
?6. 下列关于三角形的内心和外心的说法中,正确的说法为( )
①三角形的内心是三角形内切圆的圆心;②三角形的内心是三个角平分线的交点;
③三角形的外心到三边的距离相等;④三角形的外心是三边中垂线的交点.
A.①②③④ B.①②③ C.①②④ D.②③④
?
7. 如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是AB上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
?
8. 已知⊙O的半径为5,直线l和点O的距离为d?cm,若直线l与⊙O有公共点,则( )
A.d>5 B.d=5 C.d<5 D.0≤d≤5
?
9. 已知,Rt△ABC中,∠C=90?,AC=3cm,BC=4cm,则△ABC的外接圆半径和△ABC的外心与内心之间的距离分别为( )
A.5和5 B.52和52 C.52和5 D.52和12
?
10. AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC C.CD=DB D.AC?//?OD
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 ) ?
11. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是________.
?
12. ⊙O是Rt△ABC的内切圆,切点为D、E、F,若AF、BE的长分别是3和10,则内切圆的半径是________.
?
13.
(1)⊙O的直径为11cm,若圆心到一直线的距离为5.5cm,那么这条直线和圆的关系是________;
(2)如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35?,则∠P的度数是________.
?
14. 如图,在△ABC中,AB=AC,∠B=30?,以点A为圆心,以3cm为半径作⊙A,当AB=________cm时,BC与⊙A相切.
?
15. 如图所示,P为⊙O?外一点,PA,PB分别切?⊙O?于点A,B.CD切?⊙O?于点E,分别交PA,PB于点C,D,若PA=15,则△PCD的周长为________.
?16. 已知:三角形的三边长为3、4、5,则此三角形的内切圆的半径为________.
?
17. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=50?,则∠BAC=________.
?
18. 如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为________cm.
三、 解答题 (本题共计 6 小题 ,共计60分 ) ?
19. 已知⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A、B、C三点,AD=6,BD=8,CD=53,问:A、B、C三点与⊙O的位置关系.
?
20. 如图,△ABC内接于圆O,若圆的半径是2,AB=3,求sinC.
?
21. 已知⊙O为△DEF的内切圆,切点分别为A、B、C,AB=BC
求证:BE=BF;
?
22. 如图,在△ABC中,BC>AC,⊙O分别切BC、AC于E、F,D是线段BE上的一点,AD交⊙O于P、Q两点,即AP=DQ,求证:∠B=∠DAC-∠DAB.
?
23. 如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
?
24. 已知OA,OB是⊙O的半径,且OA⊥OB,垂足为O,P是射线OA上的一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交射线OA于点E.
(I)如图①,点P在线段OA上,若∠OBQ=15?,求∠AQE的大小;
(Ⅱ)如图②,点P在OA的延长线上,若∠OBQ=65?,求∠AQE的大小.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ 点A在半径为3的圆上,
∴ 点A与圆心的距离d=3.
故选B.
2.
【答案】
B
【解答】
当将⊙M水平向左平移,当点M运动到M'位置时,如图
作MC⊥OA于C点,M'H⊥OA于H,M'Q⊥MC于Q,连结M'E,
∵ ⊙M与边OB、OA相切,
∴ MM'?//?OB,MC=23,
∵ M'H⊥OA,
∴ EH=FH=12EF=12×6=3,
在Rt△EHM'中,EM'=23,
∴ HM'=EM?'2-EH2=3,
∵ M'Q⊥MC,
∴ 四边形M'QCH为矩形,
∴ CQ=M'H=3,
∴ MQ=23-3=3,
∵ ∠QMM'=∠AOB=60?,
∴ ∠QM'M=30?,
∴ M'Q=MQ3=1,
∴ MM'=2;
当将⊙M水平向左平移,当点M运动到M″位置时,如图2,
作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,
易得MC=23,M'H=3,
∵ ∠MDC=∠M″DH=∠AOB=60?,
∴ ∠HM″D=30?,∠CMD=30?,
在Rt△HM″D中,M″D=3,则DH=M″D3=1,
∴ M″D=2DH=2,
在Rt△CDM中,CM=23,则DC=MC3=2,
∴ DM=2DC=4,
∴ MM″=2+4=6,
综上所述,当⊙M平移的距离为2或6.
3.
【答案】
D
【解答】
解:∵ 圆外切等腰梯形的一腰长是8,
∴ 梯形对边和为:8+8=16,
则这个等腰梯形的上底与下底长的和为16.
故选:D.
4.
【答案】
C
【解答】
解:∵ TA,TC是圆O的切线.
∴ TA=TC,
∴ ∠TAC=∠TCA,
同理,∠TDB=∠TBD,
又∵ ∠ATC=∠BTD,
∴ ∠TAC=∠TBD,
∴ AC?//?BD,
当TA=TB时,TA=TC=TB=TD,则四边形ACBD是矩形.
当TA≠TB时,AB=CD,则四边形ACBD是等腰梯形,
故选C.
5.
【答案】
A
【解答】
解:A、根据圆的切线的定义,可知与圆仅有一个公共点的直线是切线,故选项正确;
B、垂直于圆的半径的直线,可能与圆相交或相离,故选项错误;
C、与圆心的距离等于直径的直线与圆相离,故选项错误;
D、过圆的半径外端的直线与圆相交或相切,故选项错误.
故选A.
6.
【答案】
C
【解答】
解:①三角形的内心是三角形内切圆的圆心;是三角形的内心的定义,故正确;
②∵ 三角形内切圆与各边都相切,
∴ 由切线长定理可得:三角形的内心是三个角平分线的交点;故正确;
③∵ 三角形的外心是三角形外接圆的圆心,
∴ 三角形的外心到三个顶点的距离相等;故错误;
④三角形的外心是三边中垂线的交点,正确.
∴ 正确的说法为:①②④.
故选C.
7.
【答案】
B
【解答】
解:∵ PA,PB分别和⊙O切于A,B两点,
∴ PA=PB,
∵ DE是⊙O的切线,
∴ DA=DC,EB=EC,
∵ △PDE的周长为12,
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,
∴ PA=6.
故选B.
8.
【答案】
D
【解答】
解:∵ ⊙O与直线有公共点,
∴ 直线L与圆相切或相交,
∴ 点O到直线L的距离小于或等于圆的半径,
即d≤5,
∵ d≥0,
∴ 0≤d≤5.
故选D.
9.
【答案】
B
【解答】
(2)连接ID,IE,IF,
∵ ⊙I是△ABC的内切圆,
∴ ID⊥BC,IE⊥AC,IF⊥AB,
∴ ∠CDI=∠CEI=∠C=90?,
又∵ DI=EI,
∴ 四边形CDIE是正方形.
∴ CD=CE=DI=IE(1)∵ AC=3cm,BC=4cm,由(1)知AB=5cm,
∴ △ABC的内切圆半径长r=a+b-c2,
=3+4-52
=1cm.
即DI=EI=FI=1cm(2)∴ CD=1cm.
∵ BC=4cm,
∴ BD=3cm.
∵ ⊙I是△ABC的内切圆,
∴ BD=BF=3cm.
∵ BO=52cm,
∴ OF=12cm.
在Rt△IFO中,IO=52cm(勾股定理).
∴ △ABC的外心与内心之间的距离为52cm.
故选:B.
10.
【答案】
A
【解答】
当AB=AC时,如图:连接AD,
∵ AB是⊙O的直径,
∴ AD⊥BC,
∴ CD=BD,
∵ AO=BO,
∴ OD是△ABC的中位线,
∴ OD?//?AC,
∵ DE⊥AC,
∴ DE⊥OD,
∴ DE是⊙O的切线.
所以B正确.
当CD=BD时,AO=BO,∴ OD是△ABC的中位线,
∴ OD?//?AC
∵ DE⊥AC
∴ DE⊥OD
∴ DE是⊙O的切线.
所以C正确.
当AC?//?OD时,∵ DE⊥AC,∴ DE⊥OD.
∴ DE是⊙O的切线.
所以D正确.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
相交
【解答】
解:∵ 矩形ABCD中,BC=2.8,
∴ 圆心到CD的距离为2.8.
∵ AB为直径,AB=6,
∴ 半径是3.
∵ 2.8<3,
∴ 直线DC与⊙O相交.
故答案为:相交.
12.
【答案】
2
【解答】
解:连接OE、OD,设⊙O的半径为R,
∵ ⊙O是直角三角形ABC的内切圆,
∴ BE=BF=10,AF=AD=3,∠OEC=∠C=∠ODC=90?,OE=OD,
∴ 四边形ECDO是正方形,
∴ OE=CE=CD=OD=R,
由勾股定理得:(R+10)2+(R+3)2=(10+3)2,
解得:R=2,
故答案为:2.
13.
【答案】
相切,70?.
【解答】
解:(1)∵ ⊙O的直径为11cm,圆心O到一条直线的距离为5.5cm,
∴ 直线与圆相切;
(2)根据切线的性质定理得∠PAC=90?,
∴ ∠PAB=90?-∠BAC=90?-35?=55?.
根据切线长定理得PA=PB,
所以∠PBA=∠PAB=55?,
所以∠P=70?.
14.
【答案】
6
【解答】
解:如图,过点A作AD⊥BC于点D.
∵ AB=AC,∠B=30?,
∴ AD=12AB,即AB=2AD.
又∵ BC与⊙A相切,
∴ AD就是圆A的半径,
∴ AD=3cm,
则AB=2AD=6cm.
故答案是:6.
15.
【答案】
30
【解答】
解:∵ PA,PB分别切⊙O?于A,B,
∴ PA=PB=15.
同理可知:EC=CA,DE=DB,
∴ △PDC的周长=PC+CE+DE+DP
=PC+AC+PD+DB
=PA+PB
=2PA
=30.
故答案为:30.
16.
【答案】
1
【解答】
解:如图所示:△ABC中,AC=3,BC=4,AB=5,
∵ 32+42=52,即AC2+BC2=AB2,
∴ △ABC是直角三角形,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵ CD=CE,BE=BF,AF=AD,
∵ OD⊥AC,OE⊥BC,
∴ 四边形ODCE是正方形,即CD=CE=R,
∴ AC-CD=AB-BF,即3-R=5-BF①
BC-CE=AB-AF,即4-R=BF②,
①②联立得,R=1.
故答案为:1.
17.
【答案】
25?
【解答】
解:连接OB,
∵ PA,PB是⊙O的切线,A,B为切点,
∴ ∠PAO=∠PBO=90?,
∴ ∠AOB=360?-∠P-∠PAO-∠PBO=130?,
∵ OA=OB,
∴ ∠BAC=25?.
故答案为:25?.
18.
【答案】
20
【解答】
解:∵ PA,PB是圆的切线.
∴ PA=PB
同理,AE=EC,FC=FB.
三角形PEF的周长=PE+EF+PF=PE+PF+CF+EC=PE+AE+PF+FB=PA+PB=2PA=20cm.
故答案是20.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
19.
【答案】
解:OA=OD2+AD2=62,
BO=OD2+BD2=10,
CO=OD2+CD2=111,
∵ ⊙O的半径r=10,
∴ 点A在⊙O内,点B在⊙O上,点C在⊙O外.
【解答】
解:OA=OD2+AD2=62,
BO=OD2+BD2=10,
CO=OD2+CD2=111,
∵ ⊙O的半径r=10,
∴ 点A在⊙O内,点B在⊙O上,点C在⊙O外.
20.
【答案】
解:
作直径AD,连接BD,
∵ ∠ACB和∠ADB都对弧AB,
∴ ∠ACB=∠ADB,
∵ 圆的半径是2,
∴ AD=2+2=4,
∵ AD为直径,
∴ ∠ABD=90?,
∴ sinC=sinD=ABAD=34.
【解答】
解:
作直径AD,连接BD,
∵ ∠ACB和∠ADB都对弧AB,
∴ ∠ACB=∠ADB,
∵ 圆的半径是2,
∴ AD=2+2=4,
∵ AD为直径,
∴ ∠ABD=90?,
∴ sinC=sinD=ABAD=34.
21.
【答案】
解(1)如图2,连接AC,
∵ AB=BC,
∴ AB=BC,∠EAB=∠EBA=∠FCB=∠FBC,
∴ △AEB?△CFB,
∴ BE=BF;
(2)如图2,连接AC,作DG⊥AC于G,AH⊥DF于H,
∵ DE、DF是⊙O的切线,切点分别为A,C,
∴ ∠ABC=∠DAC=∠DCA,
∴ AD=DC,
∴ AG=CG=12AC,
∴ tan∠DAG=tan∠ABC=DGAG=43,
设DG=4k,则AG=3k,
∴ AC=2AG=6k,AD=CD=5k,12×AC×DG=12×CD×AH,
∴ AH=245k,
∴ sin∠EDF=AHAD=2425.
【解答】
解(1)如图2,连接AC,
∵ AB=BC,
∴ AB=BC,∠EAB=∠EBA=∠FCB=∠FBC,
∴ △AEB?△CFB,
∴ BE=BF;
(2)如图2,连接AC,作DG⊥AC于G,AH⊥DF于H,
∵ DE、DF是⊙O的切线,切点分别为A,C,
∴ ∠ABC=∠DAC=∠DCA,
∴ AD=DC,
∴ AG=CG=12AC,
∴ tan∠DAG=tan∠ABC=DGAG=43,
设DG=4k,则AG=3k,
∴ AC=2AG=6k,AD=CD=5k,12×AC×DG=12×CD×AH,
∴ AH=245k,
∴ sin∠EDF=AHAD=2425.
22.
【答案】
证明:过点O作OH⊥AD于点H,连接OA,OD,OE,OF,
∴ PH=QH,
∵ AP=DQ,
∴ AH=DH,
∴ OA=OD,
∵ ⊙O分别切BC、AC于E、F,
∴ CF=CE,OE⊥BC,OF⊥AC,
即∠AFO=∠DEO=90?,
在Rt△AOF和Rt△DOE中,
OA=ODOF=OE,
∴ Rt△AOF?Rt△DOE(HL),
∴ AF=DE,
∴ AC=DC,
∴ ∠ADC=∠DAC,
∴ ∠B=∠ADC-∠DAB=∠DAC-∠DAB.
【解答】
证明:过点O作OH⊥AD于点H,连接OA,OD,OE,OF,
∴ PH=QH,
∵ AP=DQ,
∴ AH=DH,
∴ OA=OD,
∵ ⊙O分别切BC、AC于E、F,
∴ CF=CE,OE⊥BC,OF⊥AC,
即∠AFO=∠DEO=90?,
在Rt△AOF和Rt△DOE中,
OA=ODOF=OE,
∴ Rt△AOF?Rt△DOE(HL),
∴ AF=DE,
∴ AC=DC,
∴ ∠ADC=∠DAC,
∴ ∠B=∠ADC-∠DAB=∠DAC-∠DAB.
23.
【答案】
证明:连接OC.
∵ AB是⊙O的直径,C是⊙O上一点,
∴ ∠ACB=90?,即∠ACO+∠OCB=90?.
∵ OA=OC,∠BCD=∠A,
∴ ∠ACO=∠A=∠BCD,
∴ ∠BCD+∠OCB=90?,即∠OCD=90?,
∴ CD是⊙O的切线.
在Rt△OCD中,∠OCD=90?,OC=3,CD=4,
∴ OD=OC2+CD2=5,
∴ BD=OD-OB=5-3=2.
【解答】
证明:连接OC.
∵ AB是⊙O的直径,C是⊙O上一点,
∴ ∠ACB=90?,即∠ACO+∠OCB=90?.
∵ OA=OC,∠BCD=∠A,
∴ ∠ACO=∠A=∠BCD,
∴ ∠BCD+∠OCB=90?,即∠OCD=90?,
∴ CD是⊙O的切线.
在Rt△OCD中,∠OCD=90?,OC=3,CD=4,
∴ OD=OC2+CD2=5,
∴ BD=OD-OB=5-3=2.
24.
【答案】
(I)如图①中,连接OQ.
∵ EQ是切线,
∴ OQ⊥EQ,
∴ ∠OQE=90?,
∵ OA⊥OB,
∴ ∠AOB=90?,
∴ ∠AQB=12∠AOB=45?,
∵ OB=OQ,
∴ ∠OBQ=∠OQB=15?,
∴ ∠AQE=90?-15?-45?=30?.
(Ⅱ)如图②中,连接OQ.
∵ OB=OQ,
∴ ∠B=∠OQB=65?,
∴ ∠BOQ=50?,
∵ ∠AOB=90?,
∴ ∠AOQ=40?,
∵ OQ=OA,
∴ ∠OQA=∠OAQ=70?,
∵ EQ是切线,
∴ ∠OQE=90?,
∴ ∠AQE=90?-70?=20?.
【解答】
(I)如图①中,连接OQ.
∵ EQ是切线,
∴ OQ⊥EQ,
∴ ∠OQE=90?,
∵ OA⊥OB,
∴ ∠AOB=90?,
∴ ∠AQB=12∠AOB=45?,
∵ OB=OQ,
∴ ∠OBQ=∠OQB=15?,
∴ ∠AQE=90?-15?-45?=30?.
(Ⅱ)如图②中,连接OQ.
∵ OB=OQ,
∴ ∠B=∠OQB=65?,
∴ ∠BOQ=50?,
∵ ∠AOB=90?,
∴ ∠AOQ=40?,
∵ OQ=OA,
∴ ∠OQA=∠OAQ=70?,
∵ EQ是切线,
∴ ∠OQE=90?,
∴ ∠AQE=90?-70?=20?.
