2020-2021学年江苏省南通市如皋市高二上学期期中数学试卷 (Word版含解析)
文档属性
| 名称 | 2020-2021学年江苏省南通市如皋市高二上学期期中数学试卷 (Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 14:02:53 | ||
图片预览




文档简介
2020-2021学年江苏省南通市如皋市高二(上)期中数学试卷
一、选择题(共8小题).
1.(5分)在△ABC中,设角A,B,C所对的边长分别为a,b,c,b=4,c=2,△ABC的面积,则a等于( )
A. B. C.或 D.
2.(5分),x≤sinx的否定是( )
A.,x≤sinx B.,x>sinx
C.,x>sinx D.,x≤sinx
3.(5分)已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户.若政府计划援助这三个社区中90户低收入家庭,现采用分层随机抽样的方法决定各社区户数,则甲社区中接受援助的低收入家庭的户数为( )
A.20 B.30 C.36 D.40
4.(5分)古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于正四面体、正方体也可利用公式V=kD3求体积(在正四面体中,D表示正四面体的棱长;在正方体中,D表示棱长)假设运用此体积公式求得球(直径为a)、正四面体(正四面体棱长为a)、正方体(棱长为a)的“玉积率”分别为k1,k2,k3,那么k1:k2:k3的值为( )
A. B. C. D.
5.(5分)已知抛物线C:x2=2py(p>0)的焦点为F,抛物线C上一点P(m,1)到焦点F的距离为.则实数p值为( )
A.2 B.1 C. D.
6.(5分)设A为平面α上一点,过点A的直线AO在α平面上的射影为AB,AC为α平面内的一条直线,令∠OAC=θ,∠OAB=θ1,∠BAC=θ2,则这三个角存在一个余弦关系:cosθ=cosθ1cosθ2(其中θ1和θ2只能是锐角),称为最小张角定理.直线l与平面α所成的角是,若直线l在α内的射影与α内的直线m所成角为,则直线l与直线m所成的角是( )
A. B. C. D.
7.(5分)在三棱锥P﹣ABC中,PB=PC=AB=AC=BC=4,PA=,则异面直线PC与AB所成角的余弦值是( )
A. B. C. D.
8.(5分)已知双曲线的右焦点为F,关于原点对称的两点A、B分别在双曲线的左、右两支上,,且点C在双曲线上,则双曲线的离心率为( )
A. B. C. D.2
二、多项选择题(共4小题).
9.(5分)双曲线的右焦点为F,右准线为l,点P是双曲线C上一点,记点P到直线l的距离为d,双曲线C的离心率为e,则下列条件中是2d>PF的充分不必要条件有( )
A. B. C.e∈(1,2) D.e∈(1,3)
10.(5分)在直角梯形ABCD中,,AB=BC=1,DC=2,E为DC中点,现将△ADE沿AE折起,得到一个四棱锥D﹣ABCE,则下列命题正确的有( )
A.在△ADE沿AE折起的过程中,四棱锥D﹣ABCE体积的最大值为
B.在△ADE沿AE折起的过程中,异面直线AD与BC所成的角恒为
C.在△ADE沿AE折起的过程中,二面角A﹣EC﹣D的在大小为45°
D.在四棱锥D﹣ABCE中,当D在EC上的射影恰好为EC的中点F时,DB与平面ABCE所成的角的正切为
11.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,下列命题正确的有( )
A.若A=45°,b=4,a=4,则△ABC有两解
B.若tanA+tanB+tanC>0,则△ABC一定是锐角三角形
C.a>b是sinA>sinB是充要条件
D.若acosA=bcosB,则△ABC形状是等腰或直角三角形
12.(5分)已知正方体ABCD﹣A1B1C1D1的棱长为2,M为DD1的中点,N为正方形ABCD所在平面内一动点,则下列命题正确的有( )
A.若MN=2,则MN的中点的轨迹所围成图形的面积为π
B.若N到直线BB1与直线DC的距离相等,则N的轨迹为抛物线
C.若D1N与AB所成的角为,则N的轨迹为双曲线
D.若MN与平面ABCD所成的角为,则N的轨迹为椭圆
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)若,m≥sinx+cosx恒成立,则m的取值范围为 .
14.(5分)已知F(2,0)为椭圆的右焦点.直线与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率k=1,则椭圆C的方程为 .
15.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,若4sin2C=3sin2B+sinAsinB,,则cosC的最小值为 ,当cosC最小时,△ABC的面积为 .
16.(5分)已知菱形ABCD的边长为2,对角线BD=2,现将△ABD沿BD折起,使得二面角A﹣BD﹣C为120°,则折得几何体ABCD的外接球的表面积为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知m>2,p:方程表示焦点在y轴上的椭圆;q:方程表示双曲线.若p是q的充分不必要条件,求实数t的取值范围.
18.(12分)在①csinA=a,②sinC=2sinA,③这三个条件中有且只有一个符合题意,请选择符合题意的条件,补充在下面的问题中,并求解.
在锐角△ABC中,设角A,B,C所对的边长分别为a,b,c,_____,b=4,a=3.
(1)求C;
(2)若M为边AB上一点,且∠ACM=∠MCB,求CM的长.
19.(12分)如图在直棱柱ABC﹣A1B1C1中,AB=BC,AA1、AC、A1C1的中点分别为D、E、F.
(1)求证:AC⊥平面BEF;
(2)若异面直线AA1与BF所成的角为45°,且BC与平面BEF所成角的正弦值为,求二面角B﹣CD﹣B1的余弦值.
20.(12分)如图,四边形ABCD的四个顶点共圆,,AB=14,AD=15.
(1)求BD和sinA的值;
(2)求四边形ABCD的周长的最大值.
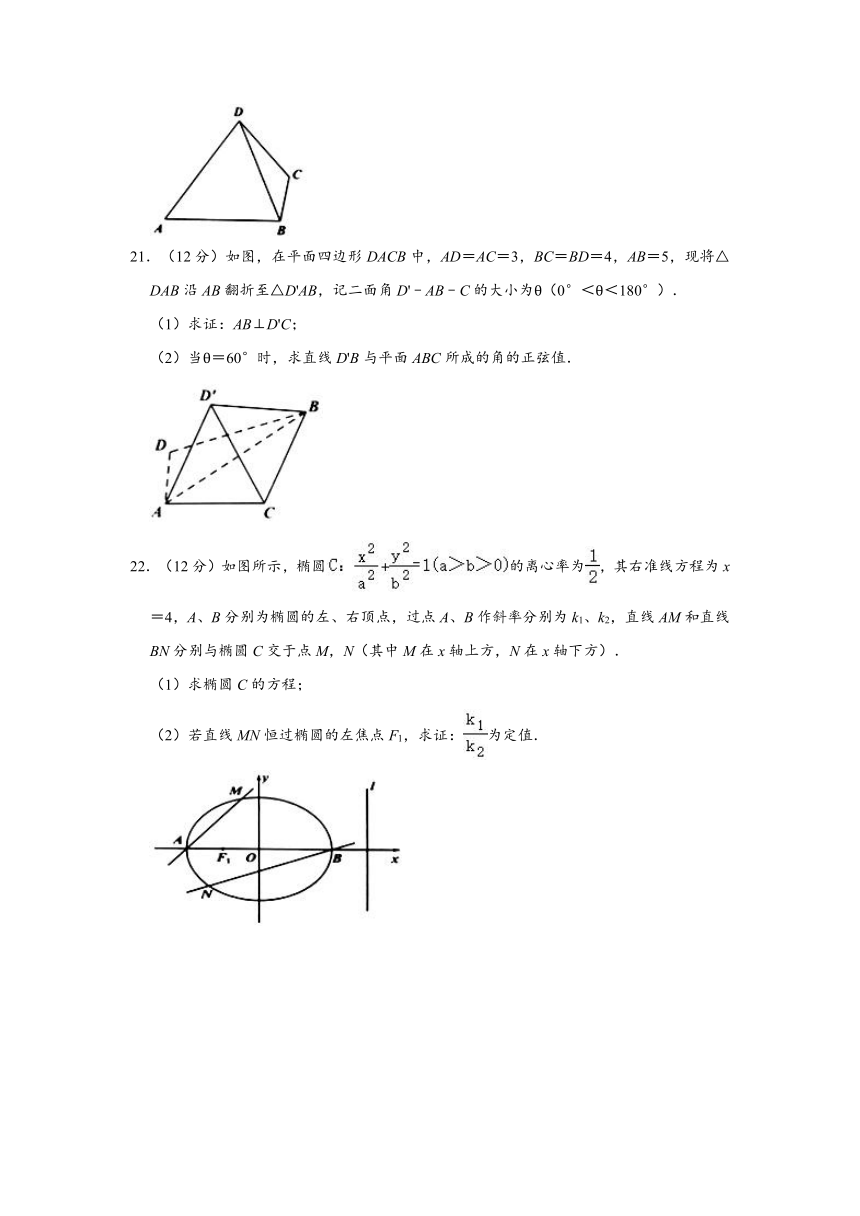
21.(12分)如图,在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,现将△DAB沿AB翻折至△D'AB,记二面角D'﹣AB﹣C的大小为θ(0°<θ<180°).
(1)求证:AB⊥D'C;
(2)当θ=60°时,求直线D'B与平面ABC所成的角的正弦值.
22.(12分)如图所示,椭圆的离心率为,其右准线方程为x=4,A、B分别为椭圆的左、右顶点,过点A、B作斜率分别为k1、k2,直线AM和直线BN分别与椭圆C交于点M,N(其中M在x轴上方,N在x轴下方).
(1)求椭圆C的方程;
(2)若直线MN恒过椭圆的左焦点F1,求证:为定值.
参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)在△ABC中,设角A,B,C所对的边长分别为a,b,c,b=4,c=2,△ABC的面积,则a等于( )
A. B. C.或 D.
解:因为b=4,c=2,△ABC的面积=bcsinA=sinA,
解得sinA=,
因为A∈(0,π),
所以A=,或,
当A=时,由余弦定理可得a===2,
当A=时,由余弦定理可得a===2,
则a的值为:2,2.
故选:C.
2.(5分),x≤sinx的否定是( )
A.,x≤sinx B.,x>sinx
C.,x>sinx D.,x≤sinx
解:命题为全称命题,则命题的否定,x>sinx,
故选:B.
3.(5分)已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户.若政府计划援助这三个社区中90户低收入家庭,现采用分层随机抽样的方法决定各社区户数,则甲社区中接受援助的低收入家庭的户数为( )
A.20 B.30 C.36 D.40
解:每个个体被抽到的概率等于=,
甲社区有360户低收入家庭,故应从甲社区中抽取低收入家庭的户数为 360×=40,
故选:D.
4.(5分)古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于正四面体、正方体也可利用公式V=kD3求体积(在正四面体中,D表示正四面体的棱长;在正方体中,D表示棱长)假设运用此体积公式求得球(直径为a)、正四面体(正四面体棱长为a)、正方体(棱长为a)的“玉积率”分别为k1,k2,k3,那么k1:k2:k3的值为( )
A. B. C. D.
解:直径为a的球的体积V1=,则k1=;
如图,
正四面体的棱长为a,则底面外接圆的半径为BF=,
正四面体的高h=,
则其体积=,得k2=;
正方体的体积,则k3=1.
∴k1:k2:k3的值为.
故选:B.
5.(5分)已知抛物线C:x2=2py(p>0)的焦点为F,抛物线C上一点P(m,1)到焦点F的距离为.则实数p值为( )
A.2 B.1 C. D.
解:抛物线C:x2=2py(p>0)的焦点为F,抛物线C上一点P(m,1)到焦点F的距离为.
可得+1=,解得p=.
故选:C.
6.(5分)设A为平面α上一点,过点A的直线AO在α平面上的射影为AB,AC为α平面内的一条直线,令∠OAC=θ,∠OAB=θ1,∠BAC=θ2,则这三个角存在一个余弦关系:cosθ=cosθ1cosθ2(其中θ1和θ2只能是锐角),称为最小张角定理.直线l与平面α所成的角是,若直线l在α内的射影与α内的直线m所成角为,则直线l与直线m所成的角是( )
A. B. C. D.
解:由题意,θ1=,θ2=,
则直线l与直线m所成的角θ满足cosθ=cosθ1cosθ2=?cos=,
又θ∈[0,],∴θ=.
故选:C.
7.(5分)在三棱锥P﹣ABC中,PB=PC=AB=AC=BC=4,PA=,则异面直线PC与AB所成角的余弦值是( )
A. B. C. D.
解:作AC的中点,作DE∥PC,DF∥AB,连接AF,EF,PF,
异面直线PC与AB所成角即DF和DE所成的角,
如图示:
,
显然DF=DE=AB=PC=2,
在等边△ABC中,AF==2,
在等边△PBC中,PF==2
而PA=,故△PAF是等边三角形,故EF==3,
在△DEF中,DF=2,DE=2,EF=3,
故cos∠EDF==﹣,
由异面直线的夹角的范围是(0°,90°],
故DF和DE所成的角是∠EDF的补角,
故DF和DE所成的角的余弦值是,
即异面直线PC与AB所成角的余弦值是,
故选:A.
8.(5分)已知双曲线的右焦点为F,关于原点对称的两点A、B分别在双曲线的左、右两支上,,且点C在双曲线上,则双曲线的离心率为( )
A. B. C. D.2
解:设双曲线的左焦点为F',连接AF',BF',CF',
由可得AF⊥BF,四边形AFBF'为矩形,
可设|BF|=t,则|FC|=3t,|BF'|=2a+t,|CF'|=3t+2a,
在直角三角形CBF'中,可得|BC|2+|BF'|2=|CF'|2,
即为(4t)2+(2a+t)2=(3t+2a)2,
解得t=a,
又在直角三角形BFF'中,|BF|2+|BF'|2=|FF'|2,
即为t2+(2a+t)2=4c2,
即为a2+9a2=10a2=4c2,
即有e==,
故选:B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.(5分)双曲线的右焦点为F,右准线为l,点P是双曲线C上一点,记点P到直线l的距离为d,双曲线C的离心率为e,则下列条件中是2d>PF的充分不必要条件有( )
A. B. C.e∈(1,2) D.e∈(1,3)
解:由双曲线的定义可得e=,即|PF|=ed,
2d>|PF|,即有2d>ed,可得1<e<2,
由充分不必要条件的定义可得A,B正确;C,D不正确.
故选:AB.
10.(5分)在直角梯形ABCD中,,AB=BC=1,DC=2,E为DC中点,现将△ADE沿AE折起,得到一个四棱锥D﹣ABCE,则下列命题正确的有( )
A.在△ADE沿AE折起的过程中,四棱锥D﹣ABCE体积的最大值为
B.在△ADE沿AE折起的过程中,异面直线AD与BC所成的角恒为
C.在△ADE沿AE折起的过程中,二面角A﹣EC﹣D的在大小为45°
D.在四棱锥D﹣ABCE中,当D在EC上的射影恰好为EC的中点F时,DB与平面ABCE所成的角的正切为
解:对于A,△ADE沿AE折起得到,四棱锥D﹣ABCE,由四棱锥底面积是固定值,要使得体积最大,
需要四棱锥的高最大,即平面DAE⊥平面ABCD,此时DE⊥CE,由已知得DE=1,
则VD﹣ABCE=S△ABCE?DE=×1×1×1=,故A正确;
对于B,在△ADE沿AE折起的过程中,AE∥BC,所以异面直线AB与AE所成的角即为AD与BC所成的角,
又AB=BC=1,DC=2,E为DC的中点,可知∠DAE=,即异面直线AD与BC所成的角恒为,故B正确;
对于C,由翻折前知,AE⊥EC,AE⊥ED,且EC∩ED=E,则AE⊥平面DEC,又AE?平面ABCE,
所以平面DEC⊥平面ABCE,即二面角二面角A﹣EC﹣D的在大小为,故C错误;
对于D,如图连接DF,BF,由选项C可知,AE⊥平面DEC,又DF?平面DEC,则AE⊥DF,
又由已知得EC⊥DF,且EC∩AE=E,则DF⊥平面ABCD,所以∠DBF为直线与平面ABCE所成的角,
在直角三角形DFB中,tan∠DBF=====,
所以DB与平面ABCE所成的角的正切为,故D正确.
故选:ABD.
11.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,下列命题正确的有( )
A.若A=45°,b=4,a=4,则△ABC有两解
B.若tanA+tanB+tanC>0,则△ABC一定是锐角三角形
C.a>b是sinA>sinB是充要条件
D.若acosA=bcosB,则△ABC形状是等腰或直角三角形
解:对于A,A=45°,b=4,a=4,所以A=B=45°,C=90°,∴c=4,△ABC只有一解,故A错;
对于B,假设△ABC为钝角△,不妨设A>,tanA<0,
∵A+B+C=π,∴tanA+tanB+tanC=tanA+tan(B+C)(1﹣tanBtanC)=tanA+(﹣tanA)(1﹣tanBtanC)=tanAtanBtanC<0,与题设tanAtanBtanC>0矛盾.
△ABC不是直角三角形,直角没有正切值,∴△ABC为锐角三角形,故选项B正确;
对于C,因为由正弦定理可得a>b?2RsinA>2RsinB?sinA>sinB,所以C正确;
对于D,由正弦定理=,化简已知等式得:sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴sin2A=sin2B,又A和B都为三角形的内角,
∴2A=2B或2A+2B=π,即A=B或A+B=,
则△ABC为等腰或直角三角形,故D正确.
故选:BCD.
12.(5分)已知正方体ABCD﹣A1B1C1D1的棱长为2,M为DD1的中点,N为正方形ABCD所在平面内一动点,则下列命题正确的有( )
A.若MN=2,则MN的中点的轨迹所围成图形的面积为π
B.若N到直线BB1与直线DC的距离相等,则N的轨迹为抛物线
C.若D1N与AB所成的角为,则N的轨迹为双曲线
D.若MN与平面ABCD所成的角为,则N的轨迹为椭圆
解:对于A,MN=2,MD=1,所以DN=,
则MN的中点到MD中点的距离为,
MN中点的轨迹为以MD中点为圆心,为半径且平行于平面ABCD的圆周,
其面积为π×=,故A错误;
对于B,BB1⊥平面ABCD,NB即为N到直线BB1的距离,
在平面ABCD内,点N到定点B的距离与到定直线DC的距离相等,
所以点N的轨迹就是以B为焦点,DC为准线的抛物线,故B正确;
对于C,如图,建立空间直角坐标系,设N(x,y,0),
=(x,y,﹣2),=(0,2,0),cos60°===,
化简得3y2﹣x2=4,即﹣=1,
所以N的轨迹为双曲线,故C正确;
对于D,MN与平面ABCD所成的角为∠MND,所以∠MND=,
则DN=,所以点N的轨迹为以D为圆心,为半径的的圆周,故D错误.
故选:BC.
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)若,m≥sinx+cosx恒成立,则m的取值范围为 [,+∞) .
解:由已知m≥sinx+cosx在(0,)上恒成立,
只需m≥(sinx+cosx)max,
又sinx+cosx=sin(x+),
当x∈(0,)时,x+∈(),
所以当x+=即x=时,(sinx+cosx)max=1=,
所以m,
故m的取值范围为:[,+∞).
14.(5分)已知F(2,0)为椭圆的右焦点.直线与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率k=1,则椭圆C的方程为 .
解:设A(x1,y1),B(x2,y2),P(x0,y0),
则,,
两式作差可得,,
即,
∵直线,直线OP的斜率k=1,
∴,即a2=3b2,①
又F(2,0),∴c=2,则a2=b2+4,②
联立①②解得a2=6,b2=2.
∴椭圆C的方程为.
故答案为:.
15.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,若4sin2C=3sin2B+sinAsinB,,则cosC的最小值为 ,当cosC最小时,△ABC的面积为 .
解:因为4sin2C=3sin2B+sinAsinB,
由正弦定理可得4c2=3b2+ab,可得c2=(3b2+ab),
由余弦定理可得cosC===+﹣≥2﹣=,当且仅当b=2a时等号成立,
所以cosC的最小值为.
当cosC最小时,cosC=,,b=2a,
由余弦定理可得14=a2+b2﹣2abcosC=a2+b2﹣ab,
所以解得a=,b=,
又sinC==,
则S△ABC=absinC=××=.
故答案为:,.
16.(5分)已知菱形ABCD的边长为2,对角线BD=2,现将△ABD沿BD折起,使得二面角A﹣BD﹣C为120°,则折得几何体ABCD的外接球的表面积为 π .
解:如图,设两三角形外心分别为O2,O3,球心为O,BD中点为O1,菱形ABCD的边长为2,对角线BD=2,
由题意知∠AO1C=120°,O1O3==,
∴OO1=,OO3=1,CO3==
∴球半径OC==,
∴四面体的外接球的表面积为S=4π×()2=π.
故答案为:π.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知m>2,p:方程表示焦点在y轴上的椭圆;q:方程表示双曲线.若p是q的充分不必要条件,求实数t的取值范围.
解:由m>2且p:方程表示焦点在y轴上的椭圆;
则2<m<4,
由m>2且q:方程表示双曲线,
则(m﹣t)(m﹣4t)<0,则t<m<4t,
若p是q的充分不必要条件,
则(2,4)?(t,4t),
则,解得:1≤t≤2,
故t的范围是[1,2].
18.(12分)在①csinA=a,②sinC=2sinA,③这三个条件中有且只有一个符合题意,请选择符合题意的条件,补充在下面的问题中,并求解.
在锐角△ABC中,设角A,B,C所对的边长分别为a,b,c,_____,b=4,a=3.
(1)求C;
(2)若M为边AB上一点,且∠ACM=∠MCB,求CM的长.
解:(1)若选①,csinA=a,
又由正弦定理,可得csinA=asinC,
所以sinC=1,
因为△ABC位锐角三角形,故C无解,不符合题意.
若选②,sinC=2sinA,由正弦定理可得c=2a,
因为b=4,a=3,可得c=6,
所以cosC===﹣<0,
因为△ABC位锐角三角形,故C无解,不符合题意.
若选③,,
可得2b2=2bccosA(1+tanA),整理可得b=ccosA+c?cosA?,
由正弦定理可得,sinB=sinCcosA+sinC?sinA,
又sinB=sin(A+C)=sinAcosC+cosAsinC,
所以可得sinAcosC=sinC?sinA,
因为sinA≠0,可得tanC=,
由C为锐角,可得C=,
(2)因为C=,b=4,a=3,
由余弦定理可得c===,
因为M为边AB上一点,且∠ACM=∠MCB=,且,AM+MB=,
解得AM=,
所以在△ACM中,由余弦定理AC2+CM2﹣2AC?CM?cos∠ACM=AM2,
可得16+CM2﹣2×=()2,
整理得CM2﹣4CM+=0,
解得CM=,或.
19.(12分)如图在直棱柱ABC﹣A1B1C1中,AB=BC,AA1、AC、A1C1的中点分别为D、E、F.
(1)求证:AC⊥平面BEF;
(2)若异面直线AA1与BF所成的角为45°,且BC与平面BEF所成角的正弦值为,求二面角B﹣CD﹣B1的余弦值.
【解答】(1)证明:∵直棱柱ABC﹣A1B1C1中,
∴BB1⊥平面ABC,
∵AC∥A1C1,AC=A1C1,
又E,F分别是AC,A1C1的中点,
∴AE=A1F,
∴四边形AEFA1是平行四边形,
∴EF∥AA1,∴EF⊥平面ABC,
又AC?平面ABC,
∴EF⊥AC,
∵AB=BC,E是AC的中点,
∴BE⊥AC,又BE∩EF=E,
∴AC⊥平面BEF.
(2)解:∵AA1∥EF,
∴∠BFE为异面直线AA1与BF所成的角,即∠BFE=45°,
∴EF=BE,
∵AC⊥平面BEF,∴∠CBE为直线BC与平面BEF所成的角,
∴sin∠CBE=,∴tan∠BCF=,∴BE=2CE,
以E为原点,以EB,EC,EF为坐标轴建立空间直角坐标系E﹣xyz,如图所示,
设CE=1,则B(2,0,0),C(0,1,0),D(0,﹣1,1),B1(2,0,2),
∴=(0,2,﹣1),=(﹣2,1,0),=(2,﹣1,2),
设平面BCD的法向量为=(x1,y1,z1),则,即,
令x1=1可得=(1,2,4),
设平面B1CD的法向量为=(x2,y2,z2),则,即,
令y2=1可得=(﹣,1,2),
∴cos<,>===,
∴二面角B﹣CD﹣B1的余弦值为.
20.(12分)如图,四边形ABCD的四个顶点共圆,,AB=14,AD=15.
(1)求BD和sinA的值;
(2)求四边形ABCD的周长的最大值.
解:(1)设BD=x,∵=,
整理得:13x2﹣140x﹣13×29=0,∴(x﹣13×(13x+29)=0,
解得:x=13,x=(舍去).
∴BD=13.
又∵在△ABD中,cosA=,
∴sinA=.
(2)∵四边形ABCD的四个顶点共圆,
∴∠BAD+∠BCD=π,∴cos∠BCD=cos(π﹣∠BAD)=﹣cosBAD=﹣,
∴在△BCD中,BD2=BC2+CD2﹣2×BC×CD,即1132=BC2+CD2﹣2×BC×CDcos∠BCD,
∴=(,
又∵BC×CD≤,当且仅当BC=CD时取等号,
∴,
∴,∴BC+CD≤,
∴AB+BC+CD+DA≤14+15+=29,
∴四边形ABCD的周长的最大值为:29.
21.(12分)如图,在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,现将△DAB沿AB翻折至△D'AB,记二面角D'﹣AB﹣C的大小为θ(0°<θ<180°).
(1)求证:AB⊥D'C;
(2)当θ=60°时,求直线D'B与平面ABC所成的角的正弦值.
【解答】(1)证明:过D′作D′O⊥AB,交AB于O,连接CO,
∵在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,
将△DAB沿AB翻折至△D'AB,
∴CO⊥AB,
∵CO∩D′O=O,∴AB⊥平面D′OC,
∵D′C?平面D′OC,∴AB⊥D'C.
(2)解:∵在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,
将△DAB沿AB翻折至△D'AB,二面角D'﹣AB﹣C的大小60°,
∴D′O=CO=D′C==,
过D′作D′E⊥平面ABC,交CO于点E,则D′E==,
连接BE,则∠D′BE是直线D'B与平面ABC所成的角,
sin∠D′BE===,
∴直线D'B与平面ABC所成的角的正弦值为.
22.(12分)如图所示,椭圆的离心率为,其右准线方程为x=4,A、B分别为椭圆的左、右顶点,过点A、B作斜率分别为k1、k2,直线AM和直线BN分别与椭圆C交于点M,N(其中M在x轴上方,N在x轴下方).
(1)求椭圆C的方程;
(2)若直线MN恒过椭圆的左焦点F1,求证:为定值.
解:(1)根据题意可得,
解得a2=4,b2=3,
所以椭圆的方程为+=1.
(2)设直线AM的方程为y=k1(x+2),M(x1,y1)
联立椭圆的方程得(3+4k12)x2+16k12x+16k12﹣12=0,
所以x1﹣2=,x1×(﹣2)=,
所以x1=,y1=k1(+2)=,
所以M(,),
设直线BN的方程为y=k2(x+2),M(x2,y2)
联立椭圆的方程得(3+4k22)x2+16k22x+16k22﹣12=0,
所以x2×2=,即x2=,
所以y2=k2(﹣2)=,
所以N(,),
又MN过点F1(﹣1,0),∥,=(,),=(,),
所以×﹣×=0,
即(k1﹣3k2)(4k1k2+3)=0,
又k1>0,k2>0,
所以4k1k2+3>0,
所以k1=3k2,即=3,
所以的定值为3.
一、选择题(共8小题).
1.(5分)在△ABC中,设角A,B,C所对的边长分别为a,b,c,b=4,c=2,△ABC的面积,则a等于( )
A. B. C.或 D.
2.(5分),x≤sinx的否定是( )
A.,x≤sinx B.,x>sinx
C.,x>sinx D.,x≤sinx
3.(5分)已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户.若政府计划援助这三个社区中90户低收入家庭,现采用分层随机抽样的方法决定各社区户数,则甲社区中接受援助的低收入家庭的户数为( )
A.20 B.30 C.36 D.40
4.(5分)古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于正四面体、正方体也可利用公式V=kD3求体积(在正四面体中,D表示正四面体的棱长;在正方体中,D表示棱长)假设运用此体积公式求得球(直径为a)、正四面体(正四面体棱长为a)、正方体(棱长为a)的“玉积率”分别为k1,k2,k3,那么k1:k2:k3的值为( )
A. B. C. D.
5.(5分)已知抛物线C:x2=2py(p>0)的焦点为F,抛物线C上一点P(m,1)到焦点F的距离为.则实数p值为( )
A.2 B.1 C. D.
6.(5分)设A为平面α上一点,过点A的直线AO在α平面上的射影为AB,AC为α平面内的一条直线,令∠OAC=θ,∠OAB=θ1,∠BAC=θ2,则这三个角存在一个余弦关系:cosθ=cosθ1cosθ2(其中θ1和θ2只能是锐角),称为最小张角定理.直线l与平面α所成的角是,若直线l在α内的射影与α内的直线m所成角为,则直线l与直线m所成的角是( )
A. B. C. D.
7.(5分)在三棱锥P﹣ABC中,PB=PC=AB=AC=BC=4,PA=,则异面直线PC与AB所成角的余弦值是( )
A. B. C. D.
8.(5分)已知双曲线的右焦点为F,关于原点对称的两点A、B分别在双曲线的左、右两支上,,且点C在双曲线上,则双曲线的离心率为( )
A. B. C. D.2
二、多项选择题(共4小题).
9.(5分)双曲线的右焦点为F,右准线为l,点P是双曲线C上一点,记点P到直线l的距离为d,双曲线C的离心率为e,则下列条件中是2d>PF的充分不必要条件有( )
A. B. C.e∈(1,2) D.e∈(1,3)
10.(5分)在直角梯形ABCD中,,AB=BC=1,DC=2,E为DC中点,现将△ADE沿AE折起,得到一个四棱锥D﹣ABCE,则下列命题正确的有( )
A.在△ADE沿AE折起的过程中,四棱锥D﹣ABCE体积的最大值为
B.在△ADE沿AE折起的过程中,异面直线AD与BC所成的角恒为
C.在△ADE沿AE折起的过程中,二面角A﹣EC﹣D的在大小为45°
D.在四棱锥D﹣ABCE中,当D在EC上的射影恰好为EC的中点F时,DB与平面ABCE所成的角的正切为
11.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,下列命题正确的有( )
A.若A=45°,b=4,a=4,则△ABC有两解
B.若tanA+tanB+tanC>0,则△ABC一定是锐角三角形
C.a>b是sinA>sinB是充要条件
D.若acosA=bcosB,则△ABC形状是等腰或直角三角形
12.(5分)已知正方体ABCD﹣A1B1C1D1的棱长为2,M为DD1的中点,N为正方形ABCD所在平面内一动点,则下列命题正确的有( )
A.若MN=2,则MN的中点的轨迹所围成图形的面积为π
B.若N到直线BB1与直线DC的距离相等,则N的轨迹为抛物线
C.若D1N与AB所成的角为,则N的轨迹为双曲线
D.若MN与平面ABCD所成的角为,则N的轨迹为椭圆
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)若,m≥sinx+cosx恒成立,则m的取值范围为 .
14.(5分)已知F(2,0)为椭圆的右焦点.直线与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率k=1,则椭圆C的方程为 .
15.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,若4sin2C=3sin2B+sinAsinB,,则cosC的最小值为 ,当cosC最小时,△ABC的面积为 .
16.(5分)已知菱形ABCD的边长为2,对角线BD=2,现将△ABD沿BD折起,使得二面角A﹣BD﹣C为120°,则折得几何体ABCD的外接球的表面积为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知m>2,p:方程表示焦点在y轴上的椭圆;q:方程表示双曲线.若p是q的充分不必要条件,求实数t的取值范围.
18.(12分)在①csinA=a,②sinC=2sinA,③这三个条件中有且只有一个符合题意,请选择符合题意的条件,补充在下面的问题中,并求解.
在锐角△ABC中,设角A,B,C所对的边长分别为a,b,c,_____,b=4,a=3.
(1)求C;
(2)若M为边AB上一点,且∠ACM=∠MCB,求CM的长.
19.(12分)如图在直棱柱ABC﹣A1B1C1中,AB=BC,AA1、AC、A1C1的中点分别为D、E、F.
(1)求证:AC⊥平面BEF;
(2)若异面直线AA1与BF所成的角为45°,且BC与平面BEF所成角的正弦值为,求二面角B﹣CD﹣B1的余弦值.
20.(12分)如图,四边形ABCD的四个顶点共圆,,AB=14,AD=15.
(1)求BD和sinA的值;
(2)求四边形ABCD的周长的最大值.
21.(12分)如图,在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,现将△DAB沿AB翻折至△D'AB,记二面角D'﹣AB﹣C的大小为θ(0°<θ<180°).
(1)求证:AB⊥D'C;
(2)当θ=60°时,求直线D'B与平面ABC所成的角的正弦值.
22.(12分)如图所示,椭圆的离心率为,其右准线方程为x=4,A、B分别为椭圆的左、右顶点,过点A、B作斜率分别为k1、k2,直线AM和直线BN分别与椭圆C交于点M,N(其中M在x轴上方,N在x轴下方).
(1)求椭圆C的方程;
(2)若直线MN恒过椭圆的左焦点F1,求证:为定值.
参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)在△ABC中,设角A,B,C所对的边长分别为a,b,c,b=4,c=2,△ABC的面积,则a等于( )
A. B. C.或 D.
解:因为b=4,c=2,△ABC的面积=bcsinA=sinA,
解得sinA=,
因为A∈(0,π),
所以A=,或,
当A=时,由余弦定理可得a===2,
当A=时,由余弦定理可得a===2,
则a的值为:2,2.
故选:C.
2.(5分),x≤sinx的否定是( )
A.,x≤sinx B.,x>sinx
C.,x>sinx D.,x≤sinx
解:命题为全称命题,则命题的否定,x>sinx,
故选:B.
3.(5分)已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户.若政府计划援助这三个社区中90户低收入家庭,现采用分层随机抽样的方法决定各社区户数,则甲社区中接受援助的低收入家庭的户数为( )
A.20 B.30 C.36 D.40
解:每个个体被抽到的概率等于=,
甲社区有360户低收入家庭,故应从甲社区中抽取低收入家庭的户数为 360×=40,
故选:D.
4.(5分)古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于正四面体、正方体也可利用公式V=kD3求体积(在正四面体中,D表示正四面体的棱长;在正方体中,D表示棱长)假设运用此体积公式求得球(直径为a)、正四面体(正四面体棱长为a)、正方体(棱长为a)的“玉积率”分别为k1,k2,k3,那么k1:k2:k3的值为( )
A. B. C. D.
解:直径为a的球的体积V1=,则k1=;
如图,
正四面体的棱长为a,则底面外接圆的半径为BF=,
正四面体的高h=,
则其体积=,得k2=;
正方体的体积,则k3=1.
∴k1:k2:k3的值为.
故选:B.
5.(5分)已知抛物线C:x2=2py(p>0)的焦点为F,抛物线C上一点P(m,1)到焦点F的距离为.则实数p值为( )
A.2 B.1 C. D.
解:抛物线C:x2=2py(p>0)的焦点为F,抛物线C上一点P(m,1)到焦点F的距离为.
可得+1=,解得p=.
故选:C.
6.(5分)设A为平面α上一点,过点A的直线AO在α平面上的射影为AB,AC为α平面内的一条直线,令∠OAC=θ,∠OAB=θ1,∠BAC=θ2,则这三个角存在一个余弦关系:cosθ=cosθ1cosθ2(其中θ1和θ2只能是锐角),称为最小张角定理.直线l与平面α所成的角是,若直线l在α内的射影与α内的直线m所成角为,则直线l与直线m所成的角是( )
A. B. C. D.
解:由题意,θ1=,θ2=,
则直线l与直线m所成的角θ满足cosθ=cosθ1cosθ2=?cos=,
又θ∈[0,],∴θ=.
故选:C.
7.(5分)在三棱锥P﹣ABC中,PB=PC=AB=AC=BC=4,PA=,则异面直线PC与AB所成角的余弦值是( )
A. B. C. D.
解:作AC的中点,作DE∥PC,DF∥AB,连接AF,EF,PF,
异面直线PC与AB所成角即DF和DE所成的角,
如图示:
,
显然DF=DE=AB=PC=2,
在等边△ABC中,AF==2,
在等边△PBC中,PF==2
而PA=,故△PAF是等边三角形,故EF==3,
在△DEF中,DF=2,DE=2,EF=3,
故cos∠EDF==﹣,
由异面直线的夹角的范围是(0°,90°],
故DF和DE所成的角是∠EDF的补角,
故DF和DE所成的角的余弦值是,
即异面直线PC与AB所成角的余弦值是,
故选:A.
8.(5分)已知双曲线的右焦点为F,关于原点对称的两点A、B分别在双曲线的左、右两支上,,且点C在双曲线上,则双曲线的离心率为( )
A. B. C. D.2
解:设双曲线的左焦点为F',连接AF',BF',CF',
由可得AF⊥BF,四边形AFBF'为矩形,
可设|BF|=t,则|FC|=3t,|BF'|=2a+t,|CF'|=3t+2a,
在直角三角形CBF'中,可得|BC|2+|BF'|2=|CF'|2,
即为(4t)2+(2a+t)2=(3t+2a)2,
解得t=a,
又在直角三角形BFF'中,|BF|2+|BF'|2=|FF'|2,
即为t2+(2a+t)2=4c2,
即为a2+9a2=10a2=4c2,
即有e==,
故选:B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.(5分)双曲线的右焦点为F,右准线为l,点P是双曲线C上一点,记点P到直线l的距离为d,双曲线C的离心率为e,则下列条件中是2d>PF的充分不必要条件有( )
A. B. C.e∈(1,2) D.e∈(1,3)
解:由双曲线的定义可得e=,即|PF|=ed,
2d>|PF|,即有2d>ed,可得1<e<2,
由充分不必要条件的定义可得A,B正确;C,D不正确.
故选:AB.
10.(5分)在直角梯形ABCD中,,AB=BC=1,DC=2,E为DC中点,现将△ADE沿AE折起,得到一个四棱锥D﹣ABCE,则下列命题正确的有( )
A.在△ADE沿AE折起的过程中,四棱锥D﹣ABCE体积的最大值为
B.在△ADE沿AE折起的过程中,异面直线AD与BC所成的角恒为
C.在△ADE沿AE折起的过程中,二面角A﹣EC﹣D的在大小为45°
D.在四棱锥D﹣ABCE中,当D在EC上的射影恰好为EC的中点F时,DB与平面ABCE所成的角的正切为
解:对于A,△ADE沿AE折起得到,四棱锥D﹣ABCE,由四棱锥底面积是固定值,要使得体积最大,
需要四棱锥的高最大,即平面DAE⊥平面ABCD,此时DE⊥CE,由已知得DE=1,
则VD﹣ABCE=S△ABCE?DE=×1×1×1=,故A正确;
对于B,在△ADE沿AE折起的过程中,AE∥BC,所以异面直线AB与AE所成的角即为AD与BC所成的角,
又AB=BC=1,DC=2,E为DC的中点,可知∠DAE=,即异面直线AD与BC所成的角恒为,故B正确;
对于C,由翻折前知,AE⊥EC,AE⊥ED,且EC∩ED=E,则AE⊥平面DEC,又AE?平面ABCE,
所以平面DEC⊥平面ABCE,即二面角二面角A﹣EC﹣D的在大小为,故C错误;
对于D,如图连接DF,BF,由选项C可知,AE⊥平面DEC,又DF?平面DEC,则AE⊥DF,
又由已知得EC⊥DF,且EC∩AE=E,则DF⊥平面ABCD,所以∠DBF为直线与平面ABCE所成的角,
在直角三角形DFB中,tan∠DBF=====,
所以DB与平面ABCE所成的角的正切为,故D正确.
故选:ABD.
11.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,下列命题正确的有( )
A.若A=45°,b=4,a=4,则△ABC有两解
B.若tanA+tanB+tanC>0,则△ABC一定是锐角三角形
C.a>b是sinA>sinB是充要条件
D.若acosA=bcosB,则△ABC形状是等腰或直角三角形
解:对于A,A=45°,b=4,a=4,所以A=B=45°,C=90°,∴c=4,△ABC只有一解,故A错;
对于B,假设△ABC为钝角△,不妨设A>,tanA<0,
∵A+B+C=π,∴tanA+tanB+tanC=tanA+tan(B+C)(1﹣tanBtanC)=tanA+(﹣tanA)(1﹣tanBtanC)=tanAtanBtanC<0,与题设tanAtanBtanC>0矛盾.
△ABC不是直角三角形,直角没有正切值,∴△ABC为锐角三角形,故选项B正确;
对于C,因为由正弦定理可得a>b?2RsinA>2RsinB?sinA>sinB,所以C正确;
对于D,由正弦定理=,化简已知等式得:sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴sin2A=sin2B,又A和B都为三角形的内角,
∴2A=2B或2A+2B=π,即A=B或A+B=,
则△ABC为等腰或直角三角形,故D正确.
故选:BCD.
12.(5分)已知正方体ABCD﹣A1B1C1D1的棱长为2,M为DD1的中点,N为正方形ABCD所在平面内一动点,则下列命题正确的有( )
A.若MN=2,则MN的中点的轨迹所围成图形的面积为π
B.若N到直线BB1与直线DC的距离相等,则N的轨迹为抛物线
C.若D1N与AB所成的角为,则N的轨迹为双曲线
D.若MN与平面ABCD所成的角为,则N的轨迹为椭圆
解:对于A,MN=2,MD=1,所以DN=,
则MN的中点到MD中点的距离为,
MN中点的轨迹为以MD中点为圆心,为半径且平行于平面ABCD的圆周,
其面积为π×=,故A错误;
对于B,BB1⊥平面ABCD,NB即为N到直线BB1的距离,
在平面ABCD内,点N到定点B的距离与到定直线DC的距离相等,
所以点N的轨迹就是以B为焦点,DC为准线的抛物线,故B正确;
对于C,如图,建立空间直角坐标系,设N(x,y,0),
=(x,y,﹣2),=(0,2,0),cos60°===,
化简得3y2﹣x2=4,即﹣=1,
所以N的轨迹为双曲线,故C正确;
对于D,MN与平面ABCD所成的角为∠MND,所以∠MND=,
则DN=,所以点N的轨迹为以D为圆心,为半径的的圆周,故D错误.
故选:BC.
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)若,m≥sinx+cosx恒成立,则m的取值范围为 [,+∞) .
解:由已知m≥sinx+cosx在(0,)上恒成立,
只需m≥(sinx+cosx)max,
又sinx+cosx=sin(x+),
当x∈(0,)时,x+∈(),
所以当x+=即x=时,(sinx+cosx)max=1=,
所以m,
故m的取值范围为:[,+∞).
14.(5分)已知F(2,0)为椭圆的右焦点.直线与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率k=1,则椭圆C的方程为 .
解:设A(x1,y1),B(x2,y2),P(x0,y0),
则,,
两式作差可得,,
即,
∵直线,直线OP的斜率k=1,
∴,即a2=3b2,①
又F(2,0),∴c=2,则a2=b2+4,②
联立①②解得a2=6,b2=2.
∴椭圆C的方程为.
故答案为:.
15.(5分)在△ABC中,角A,B,C所对的边长分别为a,b,c,若4sin2C=3sin2B+sinAsinB,,则cosC的最小值为 ,当cosC最小时,△ABC的面积为 .
解:因为4sin2C=3sin2B+sinAsinB,
由正弦定理可得4c2=3b2+ab,可得c2=(3b2+ab),
由余弦定理可得cosC===+﹣≥2﹣=,当且仅当b=2a时等号成立,
所以cosC的最小值为.
当cosC最小时,cosC=,,b=2a,
由余弦定理可得14=a2+b2﹣2abcosC=a2+b2﹣ab,
所以解得a=,b=,
又sinC==,
则S△ABC=absinC=××=.
故答案为:,.
16.(5分)已知菱形ABCD的边长为2,对角线BD=2,现将△ABD沿BD折起,使得二面角A﹣BD﹣C为120°,则折得几何体ABCD的外接球的表面积为 π .
解:如图,设两三角形外心分别为O2,O3,球心为O,BD中点为O1,菱形ABCD的边长为2,对角线BD=2,
由题意知∠AO1C=120°,O1O3==,
∴OO1=,OO3=1,CO3==
∴球半径OC==,
∴四面体的外接球的表面积为S=4π×()2=π.
故答案为:π.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知m>2,p:方程表示焦点在y轴上的椭圆;q:方程表示双曲线.若p是q的充分不必要条件,求实数t的取值范围.
解:由m>2且p:方程表示焦点在y轴上的椭圆;
则2<m<4,
由m>2且q:方程表示双曲线,
则(m﹣t)(m﹣4t)<0,则t<m<4t,
若p是q的充分不必要条件,
则(2,4)?(t,4t),
则,解得:1≤t≤2,
故t的范围是[1,2].
18.(12分)在①csinA=a,②sinC=2sinA,③这三个条件中有且只有一个符合题意,请选择符合题意的条件,补充在下面的问题中,并求解.
在锐角△ABC中,设角A,B,C所对的边长分别为a,b,c,_____,b=4,a=3.
(1)求C;
(2)若M为边AB上一点,且∠ACM=∠MCB,求CM的长.
解:(1)若选①,csinA=a,
又由正弦定理,可得csinA=asinC,
所以sinC=1,
因为△ABC位锐角三角形,故C无解,不符合题意.
若选②,sinC=2sinA,由正弦定理可得c=2a,
因为b=4,a=3,可得c=6,
所以cosC===﹣<0,
因为△ABC位锐角三角形,故C无解,不符合题意.
若选③,,
可得2b2=2bccosA(1+tanA),整理可得b=ccosA+c?cosA?,
由正弦定理可得,sinB=sinCcosA+sinC?sinA,
又sinB=sin(A+C)=sinAcosC+cosAsinC,
所以可得sinAcosC=sinC?sinA,
因为sinA≠0,可得tanC=,
由C为锐角,可得C=,
(2)因为C=,b=4,a=3,
由余弦定理可得c===,
因为M为边AB上一点,且∠ACM=∠MCB=,且,AM+MB=,
解得AM=,
所以在△ACM中,由余弦定理AC2+CM2﹣2AC?CM?cos∠ACM=AM2,
可得16+CM2﹣2×=()2,
整理得CM2﹣4CM+=0,
解得CM=,或.
19.(12分)如图在直棱柱ABC﹣A1B1C1中,AB=BC,AA1、AC、A1C1的中点分别为D、E、F.
(1)求证:AC⊥平面BEF;
(2)若异面直线AA1与BF所成的角为45°,且BC与平面BEF所成角的正弦值为,求二面角B﹣CD﹣B1的余弦值.
【解答】(1)证明:∵直棱柱ABC﹣A1B1C1中,
∴BB1⊥平面ABC,
∵AC∥A1C1,AC=A1C1,
又E,F分别是AC,A1C1的中点,
∴AE=A1F,
∴四边形AEFA1是平行四边形,
∴EF∥AA1,∴EF⊥平面ABC,
又AC?平面ABC,
∴EF⊥AC,
∵AB=BC,E是AC的中点,
∴BE⊥AC,又BE∩EF=E,
∴AC⊥平面BEF.
(2)解:∵AA1∥EF,
∴∠BFE为异面直线AA1与BF所成的角,即∠BFE=45°,
∴EF=BE,
∵AC⊥平面BEF,∴∠CBE为直线BC与平面BEF所成的角,
∴sin∠CBE=,∴tan∠BCF=,∴BE=2CE,
以E为原点,以EB,EC,EF为坐标轴建立空间直角坐标系E﹣xyz,如图所示,
设CE=1,则B(2,0,0),C(0,1,0),D(0,﹣1,1),B1(2,0,2),
∴=(0,2,﹣1),=(﹣2,1,0),=(2,﹣1,2),
设平面BCD的法向量为=(x1,y1,z1),则,即,
令x1=1可得=(1,2,4),
设平面B1CD的法向量为=(x2,y2,z2),则,即,
令y2=1可得=(﹣,1,2),
∴cos<,>===,
∴二面角B﹣CD﹣B1的余弦值为.
20.(12分)如图,四边形ABCD的四个顶点共圆,,AB=14,AD=15.
(1)求BD和sinA的值;
(2)求四边形ABCD的周长的最大值.
解:(1)设BD=x,∵=,
整理得:13x2﹣140x﹣13×29=0,∴(x﹣13×(13x+29)=0,
解得:x=13,x=(舍去).
∴BD=13.
又∵在△ABD中,cosA=,
∴sinA=.
(2)∵四边形ABCD的四个顶点共圆,
∴∠BAD+∠BCD=π,∴cos∠BCD=cos(π﹣∠BAD)=﹣cosBAD=﹣,
∴在△BCD中,BD2=BC2+CD2﹣2×BC×CD,即1132=BC2+CD2﹣2×BC×CDcos∠BCD,
∴=(,
又∵BC×CD≤,当且仅当BC=CD时取等号,
∴,
∴,∴BC+CD≤,
∴AB+BC+CD+DA≤14+15+=29,
∴四边形ABCD的周长的最大值为:29.
21.(12分)如图,在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,现将△DAB沿AB翻折至△D'AB,记二面角D'﹣AB﹣C的大小为θ(0°<θ<180°).
(1)求证:AB⊥D'C;
(2)当θ=60°时,求直线D'B与平面ABC所成的角的正弦值.
【解答】(1)证明:过D′作D′O⊥AB,交AB于O,连接CO,
∵在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,
将△DAB沿AB翻折至△D'AB,
∴CO⊥AB,
∵CO∩D′O=O,∴AB⊥平面D′OC,
∵D′C?平面D′OC,∴AB⊥D'C.
(2)解:∵在平面四边形DACB中,AD=AC=3,BC=BD=4,AB=5,
将△DAB沿AB翻折至△D'AB,二面角D'﹣AB﹣C的大小60°,
∴D′O=CO=D′C==,
过D′作D′E⊥平面ABC,交CO于点E,则D′E==,
连接BE,则∠D′BE是直线D'B与平面ABC所成的角,
sin∠D′BE===,
∴直线D'B与平面ABC所成的角的正弦值为.
22.(12分)如图所示,椭圆的离心率为,其右准线方程为x=4,A、B分别为椭圆的左、右顶点,过点A、B作斜率分别为k1、k2,直线AM和直线BN分别与椭圆C交于点M,N(其中M在x轴上方,N在x轴下方).
(1)求椭圆C的方程;
(2)若直线MN恒过椭圆的左焦点F1,求证:为定值.
解:(1)根据题意可得,
解得a2=4,b2=3,
所以椭圆的方程为+=1.
(2)设直线AM的方程为y=k1(x+2),M(x1,y1)
联立椭圆的方程得(3+4k12)x2+16k12x+16k12﹣12=0,
所以x1﹣2=,x1×(﹣2)=,
所以x1=,y1=k1(+2)=,
所以M(,),
设直线BN的方程为y=k2(x+2),M(x2,y2)
联立椭圆的方程得(3+4k22)x2+16k22x+16k22﹣12=0,
所以x2×2=,即x2=,
所以y2=k2(﹣2)=,
所以N(,),
又MN过点F1(﹣1,0),∥,=(,),=(,),
所以×﹣×=0,
即(k1﹣3k2)(4k1k2+3)=0,
又k1>0,k2>0,
所以4k1k2+3>0,
所以k1=3k2,即=3,
所以的定值为3.
同课章节目录
