新人教版八年级数学下册20.1.1平均数第1课时平均数和加权平均数教学课件
文档属性
| 名称 | 新人教版八年级数学下册20.1.1平均数第1课时平均数和加权平均数教学课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 912.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
20.1数据的集中趋势
20.1.1平均数
第1课时
平均数和加权平均数
第二十章
数据的分析
学习目标:
1.理解数据的权和加权平均数的概念,体会权的作用.
2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法.
重点:理解数据的权和加权平均数的概念.
难点:掌握加权平均数的计算方法.
农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种各用10块试验田进行试验,得到各试验田每公顷的产量如下表。根据这些数据,应为农科院选择甜玉米种子提出怎样的建议呢?
品种
各试验田每公顷产量(顿)
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
问题引领:
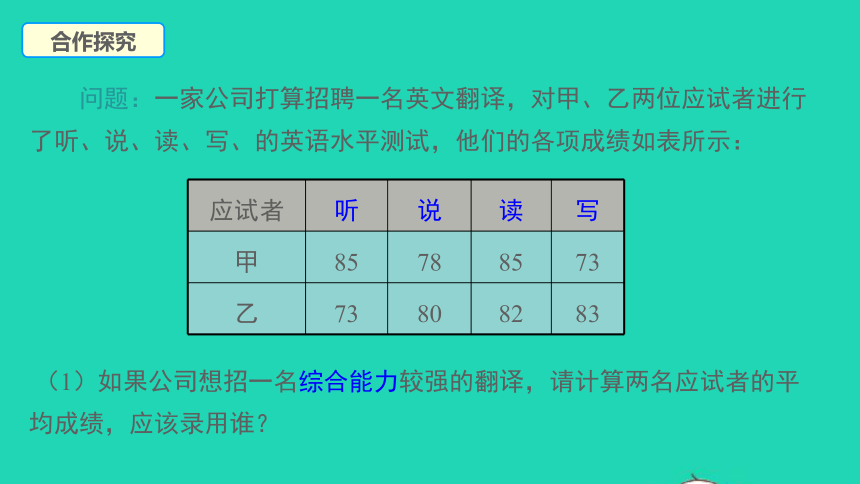
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
合作探究
乙的平均成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
我们常用平均数
表示一组数据的“平均水平”.
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:
甲的平均成绩为
,
算术平均数
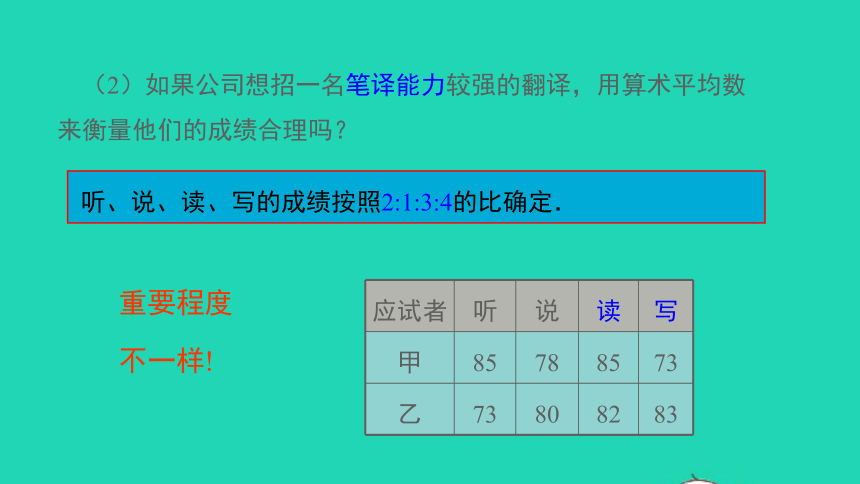
(2)如果公司想招一名笔译能力较强的翻译,用算术平均数来衡量他们的成绩合理吗?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
听、说、读、写的成绩按照2:1:3:4的比确定.
重要程度
不一样!
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
2
:
1
:
3
:
4
因为乙的成绩比甲高,所以应该录取乙.
解:
,
4
3
1
2
权
思考:能把这种加权平均数的计算方法推广到一般吗?
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫做这n个数的加权平均数.
归纳
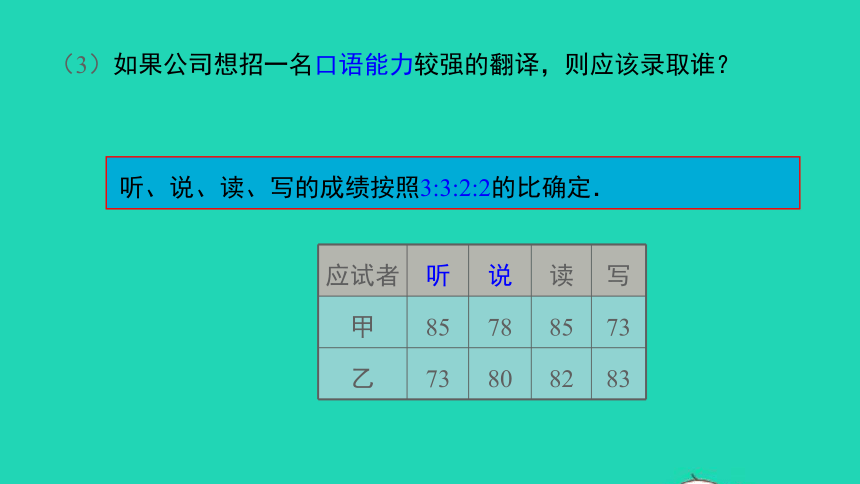
(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
听、说、读、写的成绩按照3:3:2:2的比确定.
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
(4)将问题(1)、(2)、(3)比较,你能体会到权的作用吗?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
“权”的英文是
Weight,有表示数据重要程度的意思.即数据的权能反映数据的相对“重要程度”.
例1
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
思考(1)你认为在计算选手的综合成绩时侧重于哪个方面的成绩?三项成绩的权分别是多少?
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考(2)利用加权平均数公式你能求出甲、乙的综合成绩,决出两人的名次吗?
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考两名选手的单项成绩都是两个95分与一个85分,为什么他们的最后得分不同?从中你能体会到权的作用吗?
选手A的95分是演讲能力,B的95分是演讲内容,而根据题意可知,演讲内容所占的权重比演讲能力所占的权重大,所以A的95分就不如B的95分在综合成绩中占的分值大.在此更能显示出“权”的重要性.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
练习
某公司欲招聘一名公关人员。对甲、乙两位应试者进行了面试和笔试(百分制)如下图所示,你觉得谁应该被录取?
考生
笔试
面试
甲
86
90
乙
92
83
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予他们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,------xk出现fk次(f1+f2+----+fk=n)则这几个数的算术平均数为:
例2
某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
=
≈______(岁).
答:这个跳水队运动员的平均年龄约为_____.
8
16
24
2
14
14岁
练习
下表是校女子排球队队员的年龄分布,
年龄∕岁
13
14
15
16
频数
1
4
5
2
求校女子排球队队员的平均年龄(结果取整数)
自我检测
1、在“人与自然知识竞赛”中八年级甲班5名同学的得分如下:9分、8分、9分、8分、9分。这五名同学的平均成绩:
=
。
x
2、如果数据1、4、x、5的平均数是3,那么x=
。
3、从每公斤10元的水果糖中取出5公斤,每公斤12元的软糖中取出3公斤,每公斤9元的酥糖中取出2公斤,这三种糖混在一起后,这种“杂拌糖”应定价为每公斤
元。
4、若m个数的平均数是a,n个数的平均数是b,则这m+n个数的平均数是
。
8.6
2
10.4
ma+nb
m+n
5.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元)如下表
部门
A
B
C
D
人数
1
3
7
4
利润/人
10
8
5
3
该公司每人所创年利润的平均数是_____万元.
5.4
这节课我们学习的主要内容,你都理解了吗?
加权平均数的意义
数据的权的意义
加权平均数公式
权的三种表现形式
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
加权平均数公式
ω
n
+
+
…
ω
3
ω
2
ω
1
+
+
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
…
+
ω
n
x
n
+
1.
权的三种表现形式
1、直接以数据形式给出;
2、比例形式给出;
3、百分数形式给出.
20.1数据的集中趋势
20.1.1平均数
第1课时
平均数和加权平均数
第二十章
数据的分析
学习目标:
1.理解数据的权和加权平均数的概念,体会权的作用.
2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法.
重点:理解数据的权和加权平均数的概念.
难点:掌握加权平均数的计算方法.
农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种各用10块试验田进行试验,得到各试验田每公顷的产量如下表。根据这些数据,应为农科院选择甜玉米种子提出怎样的建议呢?
品种
各试验田每公顷产量(顿)
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
问题引领:
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
合作探究
乙的平均成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
我们常用平均数
表示一组数据的“平均水平”.
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:
甲的平均成绩为
,
算术平均数
(2)如果公司想招一名笔译能力较强的翻译,用算术平均数来衡量他们的成绩合理吗?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
听、说、读、写的成绩按照2:1:3:4的比确定.
重要程度
不一样!
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
2
:
1
:
3
:
4
因为乙的成绩比甲高,所以应该录取乙.
解:
,
4
3
1
2
权
思考:能把这种加权平均数的计算方法推广到一般吗?
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫做这n个数的加权平均数.
归纳
(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
听、说、读、写的成绩按照3:3:2:2的比确定.
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
(4)将问题(1)、(2)、(3)比较,你能体会到权的作用吗?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
“权”的英文是
Weight,有表示数据重要程度的意思.即数据的权能反映数据的相对“重要程度”.
例1
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
思考(1)你认为在计算选手的综合成绩时侧重于哪个方面的成绩?三项成绩的权分别是多少?
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考(2)利用加权平均数公式你能求出甲、乙的综合成绩,决出两人的名次吗?
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考两名选手的单项成绩都是两个95分与一个85分,为什么他们的最后得分不同?从中你能体会到权的作用吗?
选手A的95分是演讲能力,B的95分是演讲内容,而根据题意可知,演讲内容所占的权重比演讲能力所占的权重大,所以A的95分就不如B的95分在综合成绩中占的分值大.在此更能显示出“权”的重要性.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
练习
某公司欲招聘一名公关人员。对甲、乙两位应试者进行了面试和笔试(百分制)如下图所示,你觉得谁应该被录取?
考生
笔试
面试
甲
86
90
乙
92
83
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予他们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,------xk出现fk次(f1+f2+----+fk=n)则这几个数的算术平均数为:
例2
某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
=
≈______(岁).
答:这个跳水队运动员的平均年龄约为_____.
8
16
24
2
14
14岁
练习
下表是校女子排球队队员的年龄分布,
年龄∕岁
13
14
15
16
频数
1
4
5
2
求校女子排球队队员的平均年龄(结果取整数)
自我检测
1、在“人与自然知识竞赛”中八年级甲班5名同学的得分如下:9分、8分、9分、8分、9分。这五名同学的平均成绩:
=
。
x
2、如果数据1、4、x、5的平均数是3,那么x=
。
3、从每公斤10元的水果糖中取出5公斤,每公斤12元的软糖中取出3公斤,每公斤9元的酥糖中取出2公斤,这三种糖混在一起后,这种“杂拌糖”应定价为每公斤
元。
4、若m个数的平均数是a,n个数的平均数是b,则这m+n个数的平均数是
。
8.6
2
10.4
ma+nb
m+n
5.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元)如下表
部门
A
B
C
D
人数
1
3
7
4
利润/人
10
8
5
3
该公司每人所创年利润的平均数是_____万元.
5.4
这节课我们学习的主要内容,你都理解了吗?
加权平均数的意义
数据的权的意义
加权平均数公式
权的三种表现形式
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
加权平均数公式
ω
n
+
+
…
ω
3
ω
2
ω
1
+
+
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
…
+
ω
n
x
n
+
1.
权的三种表现形式
1、直接以数据形式给出;
2、比例形式给出;
3、百分数形式给出.
