平方差公式
图片预览



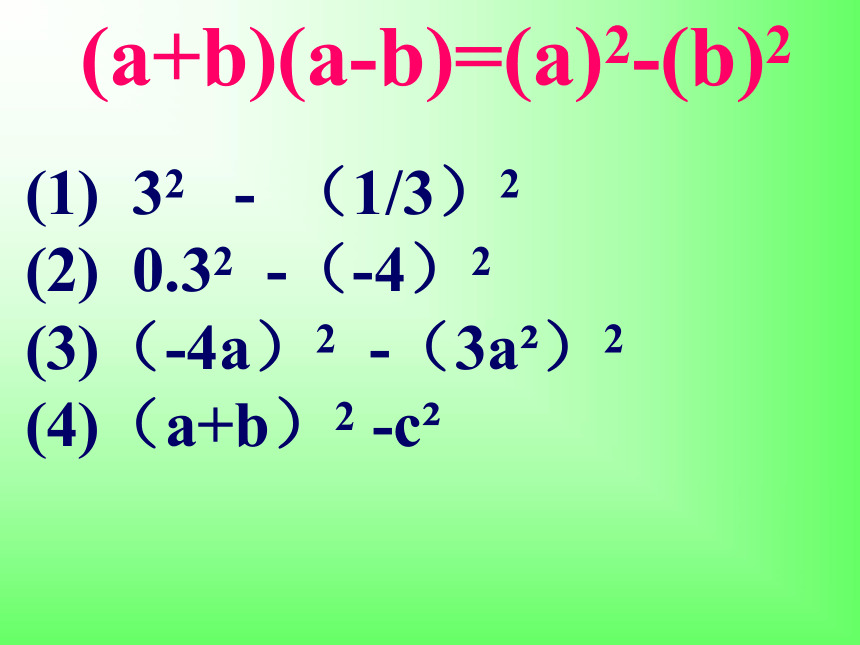

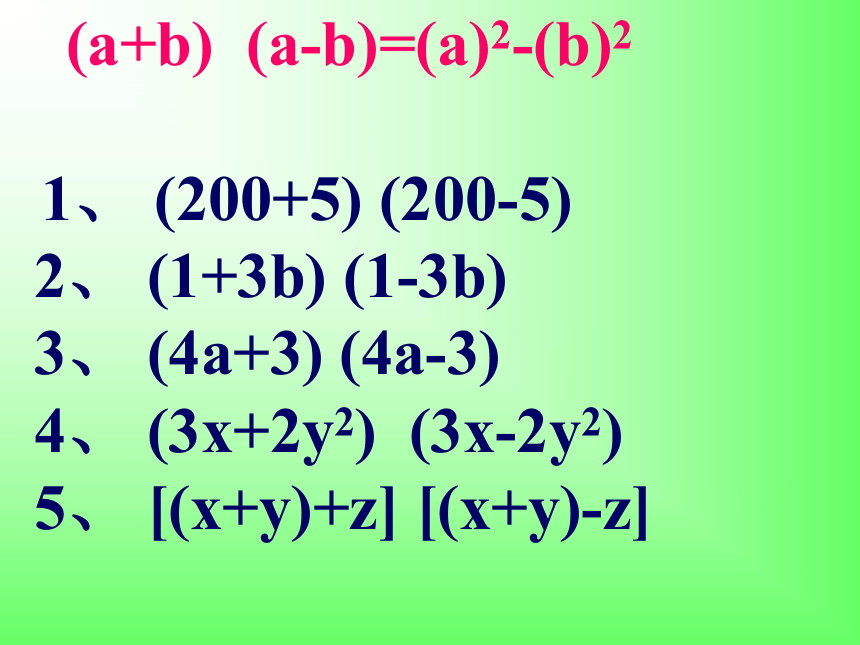
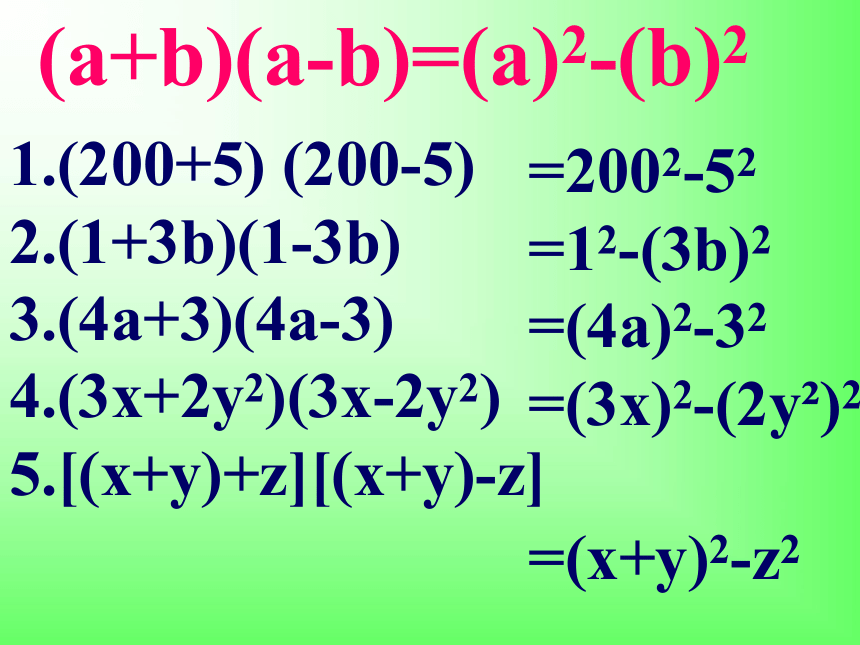


文档简介
(共27张PPT)
平 方 差 公 式
公式1 (x+a)(x+b)=x2+(a+b)x+ab
计算:(x+a)(x-a)=
x2+(a-a)x-a2=x2-a2
平方差公式 (a+b)(a-b)=a2-b2
特征
(1)两个数的和与这两个数的差之积,
等于这两个数的平方差。
(2)两个二项式相乘时,若有一
项相同,另一项符号相反,积
等于相同项平方减去相反项平方。
注:第(2)点是判断的依据和方法。
(a+b)(a-b)=a2-b2
a与b的和乘以 a 与 b 的 差 等 于 a、b的平方差
(1) 32 - (1/3)2
(2) 0.32 -(-4)2
(3)(-4a)2 -(3a )2
(4)(a+b)2 -c
(a+b)(a-b)=(a)2-(b)2
1、 a取200, b取5
2、a取1 , b膨胀为3b
3、a膨胀为4a, b取3
4、a膨胀为3x, b膨胀为2y
5、a膨胀为x+y,b缩小为z
(a+b)(a-b)=(a)2-(b)2
(a+b) (a-b)=(a)2-(b)2
1、 (200+5) (200-5)
2、 (1+3b) (1-3b)
3、 (4a+3) (4a-3)
4、 (3x+2y2) (3x-2y2)
5、 [(x+y)+z] [(x+y)-z]
=2002-52
=12-(3b)2
=(4a)2-32
=(3x)2-(2y )2
=(x+y)2-z2
1.(200+5) (200-5)
2.(1+3b)(1-3b)
3.(4a+3)(4a-3)
4.(3x+2y2)(3x-2y2)
5.[(x+y)+z][(x+y)-z]
(a+b)(a-b)=(a)2-(b)2
练习:
1、参照平方差公式“(a+b)(a-b)=a2-b2”填空。
(1)(t+s)(t-s)=____ (2)(3m+2n)(3m-2n)=_________
(3)(1+n)(1-n)=_____ (4)(10+5)(10-5)=______
t2-s2
(3m)2-(2n)2
12-n2
102-52
2、判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b) (2)(-2a+b)(-2a-b)
(3)(-a+b)(a-b) (4)(a+b)(a-c)
(是)
(否)
(否)
(是)
例题:
1、(5m+2n)(5m-2n)=
(5m)2-(2n)2
= 25m2-4n2
(a + b)( a - b )= a2 - b2
2. (1)(-4a-1)(-4a+1)
(2) [(x+y)+z][(x+y)-z]
(3)(-2a2+7)(-2a2-7)
例3 (1)(y+2)(y-2)-(3-y)(3+y)
(2)(3m-4n)(4n+3m)-(2m-3n)(2m+3n)
思考题
(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)(x16+y16)
(a+b)(a-b)=a2-b2 练习:
1、 (60-0.2)(60+0.2)
2、502*498
(a+b)(a-b)=a2-b2 3、(b+2a )(2a-b)
4、(-4a-1)(4a-1)
5、(3+2a)(-3+2a)
6、(-0.3x-1)(-0.3x+1)
7、[x+(y+1)] [x-(y+1)]
8、(a+b+c) (a+b-c)
9、(a+b+c) (a-b+c)
10、(x+3) (x-3) (x2+9) (x4+81)
(a+b)(a-b)=(a)2-(b)2
a2 - b2 =(a+b)(a-b) 逆向思维训练:
11、( )( )=n2-m2
12、 ( ) ( ) =4x2-9y2
13、(5+a)( ) =25-a
(a+b)(a-b)=(a)2-(b)2
相反为b
小结
相同为a
适当交换
合理加括
推广 !
一个长方形的长为 (√19 + √7)厘米,宽为(√19 - √7) 厘米,它的面积是多少?
(√19 + √7)(√19 -√7) =(√19)2- (√7)2
(a+b)(a-b)= (a)2-(b)2
2.(a+b+c)(a+b-c),是否可用平方差公式计
算?怎样应用公式计算?
解: (a+b+c) (a+b-c)
= [(a+b)+c] [(a+b)-c]
= (a+b)2 - c2
= (a+b) (a+b) – c2
= (a2+ab+ab+b2) – c2
= (a2+2ab+b2) – c2
= a2+2ab+b2 – c2
3.将下列各式变形为可利用平方差公式
计算的形式:
1) (a+2b+3)(a+2b-3)
2) (a+2b-3)(a-2b+3)
3) (a-2b+3)(a-2b-3)
4) (a-2b-3)(a+2b-3)
5) (3a-5b-2c)(-3a-5b+2c)
6) (x+y+m+n)(x+y-m-n)
[(a+2b)+3][(a+2b)-3]
[a+(2b-3)] [a-(2b-3)]
[(a-2b)+3] [(a-2b)-3]
[(a-3)-2b] [(a-3)+2b]
[(-5b)+(3a-2c)] [(-5b)-(3a-2c)]
[(x+y)+(m+n)][(x+y)-(m+n)]
4.下列各式哪些能用平方差公式计算?
怎样用?
1) (a-b+c)(a-b-c)
2) (a+2b-3)(a-2b+3)
3) (2x+y-z+5)(2x-y+z+5)
4) (a-b+c-d)(-a-b-c-d)
4.下列各式哪些能用平方差公式计算?
怎样用?
1) (a-b+c)(a-b-c)
解: 1) (a-b+c)(a-b-c)
= [ (a-b)+c] [ (a-b)-c ]
= (a-b)2 – c2
= (a2-2ab+b2) –c2
= a2-2ab+b2 –c2
4.下列各式哪些能用平方差公式计算?
怎样用?
2) (a+2b-3)(a-2b+3)
解:2) (a+2b-3)(a-2b+3)
= [ a+(2b-3) ] [ a-(2b-3)]
= a2- (2b-3)2
= a2- (2b-3) (2b-3)
= a2- (4b2-12b+9)
= a2- 4b2+12b-9
4.下列各式哪些能用平方差公式计算?
怎样用?
3) (2x+y-z+5)(2x-y+z+5)
4) (a-b+c-d)(-a-b-c-d)
解: 3) (2x+y-z+5)(2x-y+z+5)
= [ (2x+5)+(y-z) ] [(2x+5)-(y-z) ]
= (2x+5)2- (y-z)2 =……
解: 4) (a-b+c-d)(-a-b-c-d)
= [ (-b-d)+(a+c) ] [(-b-d)-(a+c) ]
= (-b-d)2- (a+c)2 =……
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:1) (y+2)(y-2) - (3-y)(3+y)
= (y2-4) –(9-y2)
= y2-4 –9+y2
= 2y2-13
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
= -16y2+1+12y2-12y-9
= -4y2-12y-8
解:3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
= -4(4y2- )+3(4y2+2y-6y-3)
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:4) (x+ )(x2+ )(x- )
= [(x+ )(x- )](x2+ )
= (x2- )(x2+ )
= x4-
平 方 差 公 式
公式1 (x+a)(x+b)=x2+(a+b)x+ab
计算:(x+a)(x-a)=
x2+(a-a)x-a2=x2-a2
平方差公式 (a+b)(a-b)=a2-b2
特征
(1)两个数的和与这两个数的差之积,
等于这两个数的平方差。
(2)两个二项式相乘时,若有一
项相同,另一项符号相反,积
等于相同项平方减去相反项平方。
注:第(2)点是判断的依据和方法。
(a+b)(a-b)=a2-b2
a与b的和乘以 a 与 b 的 差 等 于 a、b的平方差
(1) 32 - (1/3)2
(2) 0.32 -(-4)2
(3)(-4a)2 -(3a )2
(4)(a+b)2 -c
(a+b)(a-b)=(a)2-(b)2
1、 a取200, b取5
2、a取1 , b膨胀为3b
3、a膨胀为4a, b取3
4、a膨胀为3x, b膨胀为2y
5、a膨胀为x+y,b缩小为z
(a+b)(a-b)=(a)2-(b)2
(a+b) (a-b)=(a)2-(b)2
1、 (200+5) (200-5)
2、 (1+3b) (1-3b)
3、 (4a+3) (4a-3)
4、 (3x+2y2) (3x-2y2)
5、 [(x+y)+z] [(x+y)-z]
=2002-52
=12-(3b)2
=(4a)2-32
=(3x)2-(2y )2
=(x+y)2-z2
1.(200+5) (200-5)
2.(1+3b)(1-3b)
3.(4a+3)(4a-3)
4.(3x+2y2)(3x-2y2)
5.[(x+y)+z][(x+y)-z]
(a+b)(a-b)=(a)2-(b)2
练习:
1、参照平方差公式“(a+b)(a-b)=a2-b2”填空。
(1)(t+s)(t-s)=____ (2)(3m+2n)(3m-2n)=_________
(3)(1+n)(1-n)=_____ (4)(10+5)(10-5)=______
t2-s2
(3m)2-(2n)2
12-n2
102-52
2、判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b) (2)(-2a+b)(-2a-b)
(3)(-a+b)(a-b) (4)(a+b)(a-c)
(是)
(否)
(否)
(是)
例题:
1、(5m+2n)(5m-2n)=
(5m)2-(2n)2
= 25m2-4n2
(a + b)( a - b )= a2 - b2
2. (1)(-4a-1)(-4a+1)
(2) [(x+y)+z][(x+y)-z]
(3)(-2a2+7)(-2a2-7)
例3 (1)(y+2)(y-2)-(3-y)(3+y)
(2)(3m-4n)(4n+3m)-(2m-3n)(2m+3n)
思考题
(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)(x16+y16)
(a+b)(a-b)=a2-b2 练习:
1、 (60-0.2)(60+0.2)
2、502*498
(a+b)(a-b)=a2-b2 3、(b+2a )(2a-b)
4、(-4a-1)(4a-1)
5、(3+2a)(-3+2a)
6、(-0.3x-1)(-0.3x+1)
7、[x+(y+1)] [x-(y+1)]
8、(a+b+c) (a+b-c)
9、(a+b+c) (a-b+c)
10、(x+3) (x-3) (x2+9) (x4+81)
(a+b)(a-b)=(a)2-(b)2
a2 - b2 =(a+b)(a-b) 逆向思维训练:
11、( )( )=n2-m2
12、 ( ) ( ) =4x2-9y2
13、(5+a)( ) =25-a
(a+b)(a-b)=(a)2-(b)2
相反为b
小结
相同为a
适当交换
合理加括
推广 !
一个长方形的长为 (√19 + √7)厘米,宽为(√19 - √7) 厘米,它的面积是多少?
(√19 + √7)(√19 -√7) =(√19)2- (√7)2
(a+b)(a-b)= (a)2-(b)2
2.(a+b+c)(a+b-c),是否可用平方差公式计
算?怎样应用公式计算?
解: (a+b+c) (a+b-c)
= [(a+b)+c] [(a+b)-c]
= (a+b)2 - c2
= (a+b) (a+b) – c2
= (a2+ab+ab+b2) – c2
= (a2+2ab+b2) – c2
= a2+2ab+b2 – c2
3.将下列各式变形为可利用平方差公式
计算的形式:
1) (a+2b+3)(a+2b-3)
2) (a+2b-3)(a-2b+3)
3) (a-2b+3)(a-2b-3)
4) (a-2b-3)(a+2b-3)
5) (3a-5b-2c)(-3a-5b+2c)
6) (x+y+m+n)(x+y-m-n)
[(a+2b)+3][(a+2b)-3]
[a+(2b-3)] [a-(2b-3)]
[(a-2b)+3] [(a-2b)-3]
[(a-3)-2b] [(a-3)+2b]
[(-5b)+(3a-2c)] [(-5b)-(3a-2c)]
[(x+y)+(m+n)][(x+y)-(m+n)]
4.下列各式哪些能用平方差公式计算?
怎样用?
1) (a-b+c)(a-b-c)
2) (a+2b-3)(a-2b+3)
3) (2x+y-z+5)(2x-y+z+5)
4) (a-b+c-d)(-a-b-c-d)
4.下列各式哪些能用平方差公式计算?
怎样用?
1) (a-b+c)(a-b-c)
解: 1) (a-b+c)(a-b-c)
= [ (a-b)+c] [ (a-b)-c ]
= (a-b)2 – c2
= (a2-2ab+b2) –c2
= a2-2ab+b2 –c2
4.下列各式哪些能用平方差公式计算?
怎样用?
2) (a+2b-3)(a-2b+3)
解:2) (a+2b-3)(a-2b+3)
= [ a+(2b-3) ] [ a-(2b-3)]
= a2- (2b-3)2
= a2- (2b-3) (2b-3)
= a2- (4b2-12b+9)
= a2- 4b2+12b-9
4.下列各式哪些能用平方差公式计算?
怎样用?
3) (2x+y-z+5)(2x-y+z+5)
4) (a-b+c-d)(-a-b-c-d)
解: 3) (2x+y-z+5)(2x-y+z+5)
= [ (2x+5)+(y-z) ] [(2x+5)-(y-z) ]
= (2x+5)2- (y-z)2 =……
解: 4) (a-b+c-d)(-a-b-c-d)
= [ (-b-d)+(a+c) ] [(-b-d)-(a+c) ]
= (-b-d)2- (a+c)2 =……
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:1) (y+2)(y-2) - (3-y)(3+y)
= (y2-4) –(9-y2)
= y2-4 –9+y2
= 2y2-13
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
= -16y2+1+12y2-12y-9
= -4y2-12y-8
解:3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
= -4(4y2- )+3(4y2+2y-6y-3)
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:4) (x+ )(x2+ )(x- )
= [(x+ )(x- )](x2+ )
= (x2- )(x2+ )
= x4-
