人教版八年级数学下册 20.2 数据的波动程度 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册 20.2 数据的波动程度 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:44:56 | ||
图片预览






文档简介
第20章
20.2 数据的波动程度
教练的烦恼
?
一、情境导入,复习回顾
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
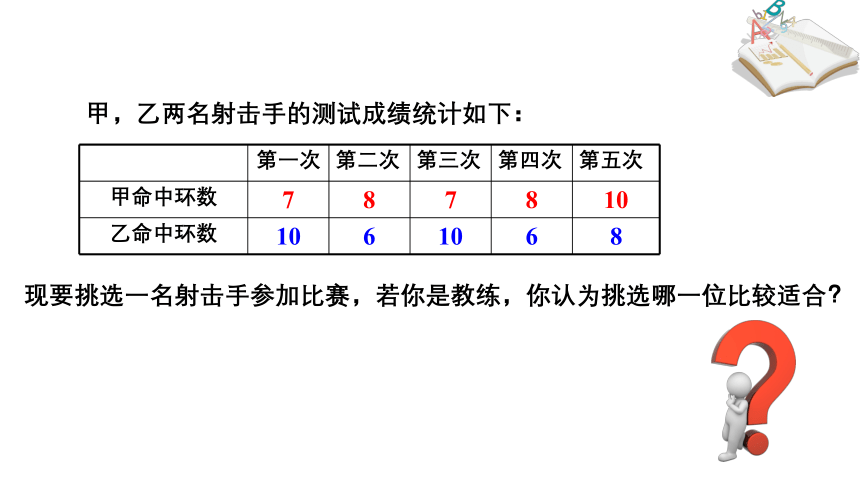
甲,乙两名射击手的测试成绩统计如下:
现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适合?
一、情境导入,复习回顾
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
⑴ 请分别计算两名射手的平均成绩;
用什么指标来衡量呢
?
(2)这两组数据的中位数和众数是多少?
甲:中位数是8 ,众数是7和8.
乙:中位数是8 ,众数是6和10.
中位数反映了数据的中间水平;
众数反映了数据的多数情况.
平均数反映了数据的平均水平.
显然,中位数和众数反映的是数据的集中趋势,不能衡量数据的波动程度.
????甲=????????(????+????+????+????+????????)=????环
?
????乙=????????(????????+????+????????+????+????)=????环
?
一、情境导入,复习回顾
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
成绩(环)
射击次序
(3) 请根据这两名射击手的成绩画出折线统计图;
数缺形时
少直观
由折线统计图可以看到,甲成绩波动较小,成绩比较稳定,乙成绩波动较大,成绩比较不稳定.故选甲参加比赛比较合适.
一、情境导入,复习回顾
0
1
2
2
3
4
5
4
6
8
10
成绩(环)
射击次序
甲
乙
波动程度
指标:? ? ?
与平均数差多少?
形缺数时
难入微
统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均数 的差的平方
分别是 ,我们用这些值的平均数,
即用
方差越大,数据的波动越大;
方差越小,数据的波动越小.
二、探索归纳,发现新知
?????????
?
?????????=
?
来衡量这组数据的波动大小,称它为这组数据的方差.记作
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
甲,乙两名射击手的测试成绩统计如下:
现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适合?
二、探索归纳,发现新知
二、探索归纳,发现新知
解:挑选甲射击手参加比赛,理由如下:
????甲=????????(????+????+????+????+????????)=????
?
????乙=????????(????????+????+????????+????+????)=????
?
????甲????=?????????????????????+?????????????+?????????????+?????????????+?????????????????=????.????
?
????乙????=?????????????????????????+?????????????+?????????????????+?????????????+?????????????=????.????
?
因为????甲???? 所以甲的成绩较稳定,挑选甲射击手参加比赛.
?
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
二、探索归纳,发现新知
例1: 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
课本P125 例1
二、探索归纳,发现新知
解:甲芭蕾舞团女演员的身高更整齐,理由如下:
????甲=????????(????????????+????????????×????+????????????×????+????????????×????+????????????)=????????????
?
????乙=????????(????????????+????????????×????+????????????×????+????????????+????????????×????)=????????????
?
????甲????=?????????????????????????????????????+?????????????????????????????+?+?????????????????????????????=????.????
?
因为????甲???? 所以甲芭蕾舞团女演员的身高更整齐.
?
????乙????=?????????????????????????????????????+?????????????????????????????+?+?????????????????????????????=????.????
?
二、探索归纳,发现新知
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
课本P127 例2
例2: 某快餐公司的香辣鸡腿很受消费者的欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿价格相同,品质相近.快餐公司决定通过检查鸡腿的重量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各抽取15个鸡腿,记录他们的质量(单位:g)如下:
根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
二、探索归纳,发现新知
解:快餐公司应该选购甲加工工厂生产的鸡腿,理由如下:
由????甲???? ?
????甲=????????????????????+????????+?+????????+????????≈????????
?
????甲????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????≈????
?
????乙=????????????????????+????????+?+????????+????????≈????????
?
????乙????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????≈????
?
由????甲≈ ????乙可知,两家工厂的鸡腿质量大致相等;
?
用样本方差估计总体方差.
三、灵活应用,能力提升
C
方差越小,数据的波动越小,成绩越稳定.
1.甲、乙两人在相同的条件下,各射靶10次,经过计算:
甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,
下列说法中不正确的是 ( )
A.甲、乙射中的总环数相同 B.甲的成绩较稳定
C.乙的成绩较稳定 D.乙的成绩波动较大
方差越大,数据的波动越大,成绩越不稳定.
三、灵活应用,能力提升
2.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}选手
甲
乙
丙
丁
方差
0.020
0.019
0.021
0.022
则这四人中发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
B
0.019<0.020<0.021<0.022
3.数据 6, 6 , 6 , 6 , 6 , 6 , 6 的方差是 .
当每个数据都相等时,方差是 0 .
0
4.数据 0, 1 , 2 , 3 , 4 的方差是 .
5.数据 1, 2 , 3 , 4 , 5 的方差是 .
三、灵活应用,能力提升
????=????
?
????????=?????????????????????+?????????????+?????????????+?????????????+?????????????=????
?
2
2
猜想
五个连续整数的方差是 .
证明
设五个连续整数分别为?????????,?????????,????, ????+????, ????+????.
?
????=????
?
????????=?????????????????+?????????+????????+????????+????????=????
?
2
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
12
13
14
15
10
16
13
11
15
11
乙
11
16
17
14
13
19
6
8
10
16
课本P128 练习3
6. 为了考察甲、乙两种小麦的长势,分别从中随机抽取10株麦苗,测得苗高(单位:cm)如下表:
(1)分别计算量两种小麦的平均身高;
三、灵活应用,能力提升
(2)哪种小麦的长势比较整齐?
二、探索归纳,发现新知
6.解:
(????)????甲=????????????(????????+????????+?+????????+????????)=????????
?
(????)????甲????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????=????.????
?
因为????甲???? ?
????????乙=????????????(????????+????????+?+????????+????????)=????????
?
答:两种小麦的平均苗高是13cm.
????乙????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????=????????
?
四、课堂小结,凝练归纳
1.方差:各数据与平均数的差的平方的平均数叫做这组数据的方差.
?????????=
?
2.方差意义:
方差越大,说明数据的波动越大; 方差越小,说明数据的波动越小.
可用样本方差估计总体方差.
而平均数、中位数、众数用来刻画数据的集中趋势.
20.2 数据的波动程度
教练的烦恼
?
一、情境导入,复习回顾
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
甲,乙两名射击手的测试成绩统计如下:
现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适合?
一、情境导入,复习回顾
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
⑴ 请分别计算两名射手的平均成绩;
用什么指标来衡量呢
?
(2)这两组数据的中位数和众数是多少?
甲:中位数是8 ,众数是7和8.
乙:中位数是8 ,众数是6和10.
中位数反映了数据的中间水平;
众数反映了数据的多数情况.
平均数反映了数据的平均水平.
显然,中位数和众数反映的是数据的集中趋势,不能衡量数据的波动程度.
????甲=????????(????+????+????+????+????????)=????环
?
????乙=????????(????????+????+????????+????+????)=????环
?
一、情境导入,复习回顾
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
成绩(环)
射击次序
(3) 请根据这两名射击手的成绩画出折线统计图;
数缺形时
少直观
由折线统计图可以看到,甲成绩波动较小,成绩比较稳定,乙成绩波动较大,成绩比较不稳定.故选甲参加比赛比较合适.
一、情境导入,复习回顾
0
1
2
2
3
4
5
4
6
8
10
成绩(环)
射击次序
甲
乙
波动程度
指标:? ? ?
与平均数差多少?
形缺数时
难入微
统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均数 的差的平方
分别是 ,我们用这些值的平均数,
即用
方差越大,数据的波动越大;
方差越小,数据的波动越小.
二、探索归纳,发现新知
?????????
?
?????????=
?
来衡量这组数据的波动大小,称它为这组数据的方差.记作
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
甲,乙两名射击手的测试成绩统计如下:
现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适合?
二、探索归纳,发现新知
二、探索归纳,发现新知
解:挑选甲射击手参加比赛,理由如下:
????甲=????????(????+????+????+????+????????)=????
?
????乙=????????(????????+????+????????+????+????)=????
?
????甲????=?????????????????????+?????????????+?????????????+?????????????+?????????????????=????.????
?
????乙????=?????????????????????????+?????????????+?????????????????+?????????????+?????????????=????.????
?
因为????甲???? 所以甲的成绩较稳定,挑选甲射击手参加比赛.
?
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
7
8
10
乙命中环数
10
6
10
6
8
二、探索归纳,发现新知
例1: 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
课本P125 例1
二、探索归纳,发现新知
解:甲芭蕾舞团女演员的身高更整齐,理由如下:
????甲=????????(????????????+????????????×????+????????????×????+????????????×????+????????????)=????????????
?
????乙=????????(????????????+????????????×????+????????????×????+????????????+????????????×????)=????????????
?
????甲????=?????????????????????????????????????+?????????????????????????????+?+?????????????????????????????=????.????
?
因为????甲???? 所以甲芭蕾舞团女演员的身高更整齐.
?
????乙????=?????????????????????????????????????+?????????????????????????????+?+?????????????????????????????=????.????
?
二、探索归纳,发现新知
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
课本P127 例2
例2: 某快餐公司的香辣鸡腿很受消费者的欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿价格相同,品质相近.快餐公司决定通过检查鸡腿的重量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各抽取15个鸡腿,记录他们的质量(单位:g)如下:
根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
二、探索归纳,发现新知
解:快餐公司应该选购甲加工工厂生产的鸡腿,理由如下:
由????甲???? ?
????甲=????????????????????+????????+?+????????+????????≈????????
?
????甲????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????≈????
?
????乙=????????????????????+????????+?+????????+????????≈????????
?
????乙????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????≈????
?
由????甲≈ ????乙可知,两家工厂的鸡腿质量大致相等;
?
用样本方差估计总体方差.
三、灵活应用,能力提升
C
方差越小,数据的波动越小,成绩越稳定.
1.甲、乙两人在相同的条件下,各射靶10次,经过计算:
甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,
下列说法中不正确的是 ( )
A.甲、乙射中的总环数相同 B.甲的成绩较稳定
C.乙的成绩较稳定 D.乙的成绩波动较大
方差越大,数据的波动越大,成绩越不稳定.
三、灵活应用,能力提升
2.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}选手
甲
乙
丙
丁
方差
0.020
0.019
0.021
0.022
则这四人中发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
B
0.019<0.020<0.021<0.022
3.数据 6, 6 , 6 , 6 , 6 , 6 , 6 的方差是 .
当每个数据都相等时,方差是 0 .
0
4.数据 0, 1 , 2 , 3 , 4 的方差是 .
5.数据 1, 2 , 3 , 4 , 5 的方差是 .
三、灵活应用,能力提升
????=????
?
????????=?????????????????????+?????????????+?????????????+?????????????+?????????????=????
?
2
2
猜想
五个连续整数的方差是 .
证明
设五个连续整数分别为?????????,?????????,????, ????+????, ????+????.
?
????=????
?
????????=?????????????????+?????????+????????+????????+????????=????
?
2
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
12
13
14
15
10
16
13
11
15
11
乙
11
16
17
14
13
19
6
8
10
16
课本P128 练习3
6. 为了考察甲、乙两种小麦的长势,分别从中随机抽取10株麦苗,测得苗高(单位:cm)如下表:
(1)分别计算量两种小麦的平均身高;
三、灵活应用,能力提升
(2)哪种小麦的长势比较整齐?
二、探索归纳,发现新知
6.解:
(????)????甲=????????????(????????+????????+?+????????+????????)=????????
?
(????)????甲????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????=????.????
?
因为????甲???? ?
????????乙=????????????(????????+????????+?+????????+????????)=????????
?
答:两种小麦的平均苗高是13cm.
????乙????=?????????????????????????????????+?????????????????????+?+?????????????????????+?????????????????????=????????
?
四、课堂小结,凝练归纳
1.方差:各数据与平均数的差的平方的平均数叫做这组数据的方差.
?????????=
?
2.方差意义:
方差越大,说明数据的波动越大; 方差越小,说明数据的波动越小.
可用样本方差估计总体方差.
而平均数、中位数、众数用来刻画数据的集中趋势.
