人教版八年级数学下册《 20.1.1平均数》课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册《 20.1.1平均数》课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
第20章
20.1.1 平均数
一、情境导入,复习回顾
1.计算6,7,8,9,10的平均数.
2. 计算6,7,8,8,7,9,10,7,6,9的平均数.
????+????+????+????+????+????+????????+????+????+????????????=7.7
?
解:
方法一
方法二
{5940675A-B579-460E-94D1-54222C63F5DA}数据
6
7
8
9
10
个数
2
3
2
2
1
????+????+????+????+????????????=8
?
????×2+????×3+????×2+????×2+????????×1????????=7.7
?
解:
一、情境导入,复习回顾
算术平均数
一般地,对于n个数x1,x2,…,xn,
x1+x2+…+xn????
叫做这n个数的算术平均数,简称平均数,记作???? ,读作x拔.
?
生活中我们常用平均数表示一组数的平均水平.
探究1:一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如表所示:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
二、探索归纳,发现新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
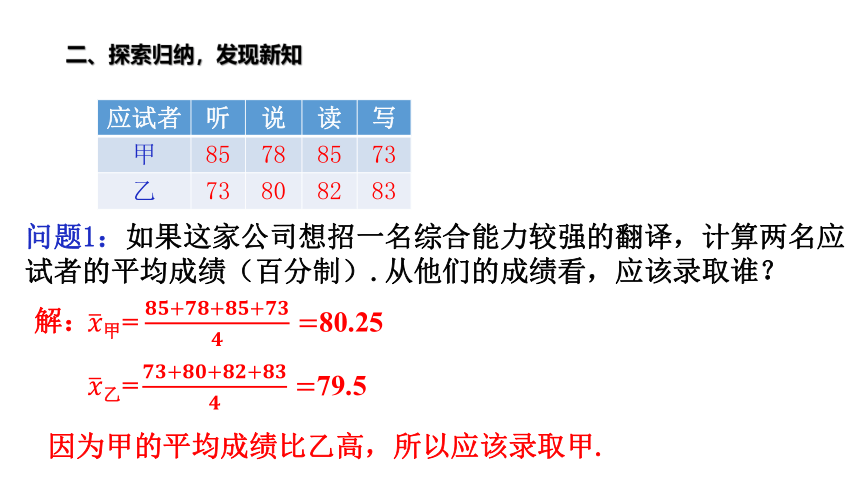
问题1:如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:
????甲= ????????+????????+????????+????????????=80.25
?
????乙= ????????+????????+????????+????????????=79.5
?
因为甲的平均成绩比乙高,所以应该录取甲.
二、探索归纳,发现新知
二、探索归纳,发现新知
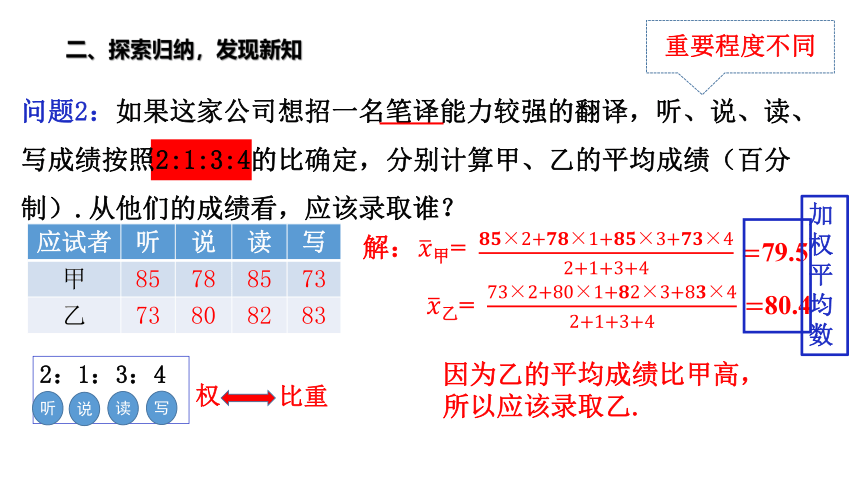
问题2:如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:1:3:4的比确定,分别计算甲、乙的平均成绩(百分制).从他们的成绩看,应该录取谁?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:
????甲=
?
????????×2+????????×1+????????×3+????????×42+1+3+4=79.5
?
????乙= 73×2+80×1+????2×3+8????×42+1+3+4=80.4
?
因为乙的平均成绩比甲高,
所以应该录取乙.
2:1:3:4
听
说
读
写
权
加权平均数
重要程度不同
比重
二、探索归纳,发现新知
问题3:
若n个数据x1,x2,…,xn的权分别为????????,????????,…,????????,这n个数据的平均数该如何计算?
?
一般地,若n个数据x1,x2,…,xn的权分别????????,????????,…,????????,则
?
x1????????+x2????????+…+x????????????????????+????????+…+????????
?
叫做这n个数的加权平均数.
权的英文是weight ,有表示数据重要程度的意思.
二、探索归纳,发现新知
问题4:如果这家公司想招一名口译能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
与问题1,问题2相比较,你能体会到权的作用吗?
解:
????甲=????????×????+????????×????+????????×????+????????×????????+????+????+????=80.5
?
????乙=73×????+80×????+82×????+83×????????+????+????+????=78.9
?
因为甲的平均成绩比乙高,所以应该录取甲.
同样的一组数据.如果规定的权变化,则加权平均数随之改变.
二、探索归纳,发现新知
变式
如果听占20%,说占10%,读占30%,写占40%,应该录取谁呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:
????乙=73×????????%+80×????????%+82×????????%+83×????????%????????%+????????%+????????%+????????%=80.4
?
????甲=85×????????%+78×????????%+85×????????%+73×????????%????????%+????????%+????????%+????????%=79.5
?
因为乙的平均成绩比甲高,所以应该录取乙.
百分数
比例
权
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,如下表所示.这天5路公共汽车平均每班的载客量是多少(结果取整数)?
三、灵活应用,能力提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}载客量
组中值
频数
1≤x<21
11
3
21≤x<41
31
5
41≤x<61
51
20
61≤x<81
71
22
81≤x<101
91
18
101≤x<121
111
15
数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数.例如,小组1≤x<21的组中值为????+????????????=11.
?
探究2:
三、灵活应用,能力提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}载客量
组中值
频数
1≤x<21
11
3
21≤x<41
31
5
41≤x<61
51
20
61≤x<81
71
22
81≤x<101
91
18
101≤x<121
111
15
解:这天5路公共汽车平均每班的载客量是
????=????????×????+????????×????+????????×????????+????????×????????+????????×????????+????????????×????????????+????+????????+????????+????????+????????≈????3(人)
?
权
比例
百分数
频数
答:这天5路公共汽车平均每班的载客量约是73人.
三、灵活应用,能力提升
例题1.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如表所示,请确定两人的名次.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
解:选手A的最后得分是
????????×????????%+????????×????????%+????????×????????%????????%+????????%+????????%=90,
?
选手B的最后得分是
????????×????????%+????????×????????%+????????×????????%????????%+????????%+????????%=91.
?
由上可知选手B获得第一名,选手A获得第二名.
例题2.某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄.(结果取整数)
三、灵活应用,能力提升
在求k个数的平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n),那么这k个数的平均数
????=????????????????+????????????????…+????????????????????
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
?
????=????????×????+????????×????????+????????×????????+????????×????????+????????+????????+????≈????4(岁)
?
解:这个跳水队运动员的平均年龄为
8
16
24
2
答:这个跳水队运动员的平均年龄约14岁。
例题3.某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡.它们的使用寿命,如表20-4所示.这批灯泡的平均使用寿命是多少?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}使用寿命
600≤x<1000
1000≤x<1400
1400≤x<1800
1800≤x<2200
2200≤x<2600
灯泡只数
5
10
12
17
6
分析:抽出的50只灯泡的使用寿命组成一个样本.可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
解:根据表20-4,可以得出各小组的组中值,于是
表20-4
????=????????????×????+????????????????×????????+????????????????×????????+????????????????×????????+????????????????×????????????=1672
?
即样本的平均数为1672.
因此,可以估计这批灯泡的平均使用寿命大约是1672小时.
用全面调查的方法考察这批灯泡的平均使用寿命合适?
三、灵活应用,能力提升
四、课堂小结,凝练归纳
两种平均数的求法:
算术平均数
加权平均数
“权”的意义:各个数据的重要程度,权衡轻重或分量大小.
加权平均数中的“权”的三种表现形式:
(1)比例
(2)百分比
(3)频数(数据的出现次数)
用样本的平均值估计总体的平均值
五、课后练习,拓展提升
1.某公司欲招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如下表所示.
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予它们 6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
面试
笔试
甲
86
90
乙
92
83
五、课后练习,拓展提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
面试
笔试
甲
86
90
乙
92
83
1.
解:(1)????甲=????????+????????????=88(分),
?
????乙=????????×6+????????×46+4=88.4(分).
?
因为甲的平均成绩比乙高,所以录取甲.
(2)????甲=????????×6+????????×46+4=87.6(分),
?
????乙=????????+????????????=87.5(分).
?
因为乙的平均成绩比甲高,所以录取乙.
五、课后练习,拓展提升
2.下表是校女子排球队队员的年龄分布.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄/岁
13
14
15
16
频数
1
4
5
2
求校女子排球队队员的平均年龄(结果取整数).
解:校排球队队员的平均年龄为
????=????????×????+????????×????+????????×????+????????×????????+????+????+????≈????5(岁)
?
答:校排球队队员的平均年龄约为15岁.
五、课后练习,拓展提升
3.某地区随机抽取若干名八年级学生进行地理会考模拟测试,并对测试进行了统计,具体统计结果如表:
{5940675A-B579-460E-94D1-54222C63F5DA}分数
90<x≤100
80<x≤90
70<x≤80
60<x≤70
0<x≤60
人数
100
200
80
80
40
(1)本次抽样调查共测试了 名学生.
(2)试计算抽取学生地理会考模拟测试的平均成绩.
(2)解:抽取学生地理会考模式测试的平均成绩为
????=????????×????????????+????????×????????????+????????×????????+????????×????????+????????×????????????????????=77.8(分)
?
500
答:抽取学生地理会考模式测试的平均成绩为77.8分.
20.1.1 平均数
一、情境导入,复习回顾
1.计算6,7,8,9,10的平均数.
2. 计算6,7,8,8,7,9,10,7,6,9的平均数.
????+????+????+????+????+????+????????+????+????+????????????=7.7
?
解:
方法一
方法二
{5940675A-B579-460E-94D1-54222C63F5DA}数据
6
7
8
9
10
个数
2
3
2
2
1
????+????+????+????+????????????=8
?
????×2+????×3+????×2+????×2+????????×1????????=7.7
?
解:
一、情境导入,复习回顾
算术平均数
一般地,对于n个数x1,x2,…,xn,
x1+x2+…+xn????
叫做这n个数的算术平均数,简称平均数,记作???? ,读作x拔.
?
生活中我们常用平均数表示一组数的平均水平.
探究1:一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如表所示:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
二、探索归纳,发现新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
问题1:如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:
????甲= ????????+????????+????????+????????????=80.25
?
????乙= ????????+????????+????????+????????????=79.5
?
因为甲的平均成绩比乙高,所以应该录取甲.
二、探索归纳,发现新知
二、探索归纳,发现新知
问题2:如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:1:3:4的比确定,分别计算甲、乙的平均成绩(百分制).从他们的成绩看,应该录取谁?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:
????甲=
?
????????×2+????????×1+????????×3+????????×42+1+3+4=79.5
?
????乙= 73×2+80×1+????2×3+8????×42+1+3+4=80.4
?
因为乙的平均成绩比甲高,
所以应该录取乙.
2:1:3:4
听
说
读
写
权
加权平均数
重要程度不同
比重
二、探索归纳,发现新知
问题3:
若n个数据x1,x2,…,xn的权分别为????????,????????,…,????????,这n个数据的平均数该如何计算?
?
一般地,若n个数据x1,x2,…,xn的权分别????????,????????,…,????????,则
?
x1????????+x2????????+…+x????????????????????+????????+…+????????
?
叫做这n个数的加权平均数.
权的英文是weight ,有表示数据重要程度的意思.
二、探索归纳,发现新知
问题4:如果这家公司想招一名口译能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
与问题1,问题2相比较,你能体会到权的作用吗?
解:
????甲=????????×????+????????×????+????????×????+????????×????????+????+????+????=80.5
?
????乙=73×????+80×????+82×????+83×????????+????+????+????=78.9
?
因为甲的平均成绩比乙高,所以应该录取甲.
同样的一组数据.如果规定的权变化,则加权平均数随之改变.
二、探索归纳,发现新知
变式
如果听占20%,说占10%,读占30%,写占40%,应该录取谁呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:
????乙=73×????????%+80×????????%+82×????????%+83×????????%????????%+????????%+????????%+????????%=80.4
?
????甲=85×????????%+78×????????%+85×????????%+73×????????%????????%+????????%+????????%+????????%=79.5
?
因为乙的平均成绩比甲高,所以应该录取乙.
百分数
比例
权
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,如下表所示.这天5路公共汽车平均每班的载客量是多少(结果取整数)?
三、灵活应用,能力提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}载客量
组中值
频数
1≤x<21
11
3
21≤x<41
31
5
41≤x<61
51
20
61≤x<81
71
22
81≤x<101
91
18
101≤x<121
111
15
数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数.例如,小组1≤x<21的组中值为????+????????????=11.
?
探究2:
三、灵活应用,能力提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}载客量
组中值
频数
1≤x<21
11
3
21≤x<41
31
5
41≤x<61
51
20
61≤x<81
71
22
81≤x<101
91
18
101≤x<121
111
15
解:这天5路公共汽车平均每班的载客量是
????=????????×????+????????×????+????????×????????+????????×????????+????????×????????+????????????×????????????+????+????????+????????+????????+????????≈????3(人)
?
权
比例
百分数
频数
答:这天5路公共汽车平均每班的载客量约是73人.
三、灵活应用,能力提升
例题1.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如表所示,请确定两人的名次.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
解:选手A的最后得分是
????????×????????%+????????×????????%+????????×????????%????????%+????????%+????????%=90,
?
选手B的最后得分是
????????×????????%+????????×????????%+????????×????????%????????%+????????%+????????%=91.
?
由上可知选手B获得第一名,选手A获得第二名.
例题2.某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄.(结果取整数)
三、灵活应用,能力提升
在求k个数的平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n),那么这k个数的平均数
????=????????????????+????????????????…+????????????????????
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
?
????=????????×????+????????×????????+????????×????????+????????×????????+????????+????????+????≈????4(岁)
?
解:这个跳水队运动员的平均年龄为
8
16
24
2
答:这个跳水队运动员的平均年龄约14岁。
例题3.某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡.它们的使用寿命,如表20-4所示.这批灯泡的平均使用寿命是多少?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}使用寿命
600≤x<1000
1000≤x<1400
1400≤x<1800
1800≤x<2200
2200≤x<2600
灯泡只数
5
10
12
17
6
分析:抽出的50只灯泡的使用寿命组成一个样本.可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
解:根据表20-4,可以得出各小组的组中值,于是
表20-4
????=????????????×????+????????????????×????????+????????????????×????????+????????????????×????????+????????????????×????????????=1672
?
即样本的平均数为1672.
因此,可以估计这批灯泡的平均使用寿命大约是1672小时.
用全面调查的方法考察这批灯泡的平均使用寿命合适?
三、灵活应用,能力提升
四、课堂小结,凝练归纳
两种平均数的求法:
算术平均数
加权平均数
“权”的意义:各个数据的重要程度,权衡轻重或分量大小.
加权平均数中的“权”的三种表现形式:
(1)比例
(2)百分比
(3)频数(数据的出现次数)
用样本的平均值估计总体的平均值
五、课后练习,拓展提升
1.某公司欲招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如下表所示.
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予它们 6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
面试
笔试
甲
86
90
乙
92
83
五、课后练习,拓展提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}应试者
面试
笔试
甲
86
90
乙
92
83
1.
解:(1)????甲=????????+????????????=88(分),
?
????乙=????????×6+????????×46+4=88.4(分).
?
因为甲的平均成绩比乙高,所以录取甲.
(2)????甲=????????×6+????????×46+4=87.6(分),
?
????乙=????????+????????????=87.5(分).
?
因为乙的平均成绩比甲高,所以录取乙.
五、课后练习,拓展提升
2.下表是校女子排球队队员的年龄分布.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄/岁
13
14
15
16
频数
1
4
5
2
求校女子排球队队员的平均年龄(结果取整数).
解:校排球队队员的平均年龄为
????=????????×????+????????×????+????????×????+????????×????????+????+????+????≈????5(岁)
?
答:校排球队队员的平均年龄约为15岁.
五、课后练习,拓展提升
3.某地区随机抽取若干名八年级学生进行地理会考模拟测试,并对测试进行了统计,具体统计结果如表:
{5940675A-B579-460E-94D1-54222C63F5DA}分数
90<x≤100
80<x≤90
70<x≤80
60<x≤70
0<x≤60
人数
100
200
80
80
40
(1)本次抽样调查共测试了 名学生.
(2)试计算抽取学生地理会考模拟测试的平均成绩.
(2)解:抽取学生地理会考模式测试的平均成绩为
????=????????×????????????+????????×????????????+????????×????????+????????×????????+????????×????????????????????=77.8(分)
?
500
答:抽取学生地理会考模式测试的平均成绩为77.8分.
