人教版八年级数学下册《19.3课题学习 选择方案》课件(共15张PPT)
文档属性
| 名称 | 人教版八年级数学下册《19.3课题学习 选择方案》课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:29:29 | ||
图片预览






文档简介
第19章
19.3 课题学习 选择方案
情境导入,复习回顾
小明报装宽带上网业务,每月的使用费为 30 元,包时上网 25 小时,每月超出包时的部分每分钟收取0.05元的超时费,设月上网时间为 x 小时,收费 y1 元,请你写出 y1 关于x的函数解析式.
当0≤ x ≤25时,y1= 30 ;
当 x>25时,
y1=30 + 0.05×60(x -25)= 3 x -45
费用
月使用费
超时费
=
+
30
超时费
=
超时时间
×
超时使用价格
(x-25)
0.05×60
×
0.05×60
(x-25)
情境导入,复习回顾
小明报装宽带上网业务,每月的使用费为 30 元,包时上网 25 小时,每月超出包时的部分按每分钟收取0.05元的超时费,设月上网时间为 x 小时,收费 y1 元,请你写出 y1 关于x的函数解析式.
当0≤ x ≤25时,y1= 30 ;
当 x>25时,
合起来可写为:
50
50
y2
y2
y1= 3 x -45
情境导入,复习回顾
小明报装宽带上网业务,每月的使用费为 30 元,包时上网 25 小时,每月超出包时的部分按每分钟收取0.05元的超时费,设月上网时间为 x 小时,收费 y1 元,请你写出 y1 关于x的函数解析式.
50
50
y2
y2
当0≤ x ≤50时,y2=50;
当 x>50时,y2=50+0.05×60(x -50)=3x -100.
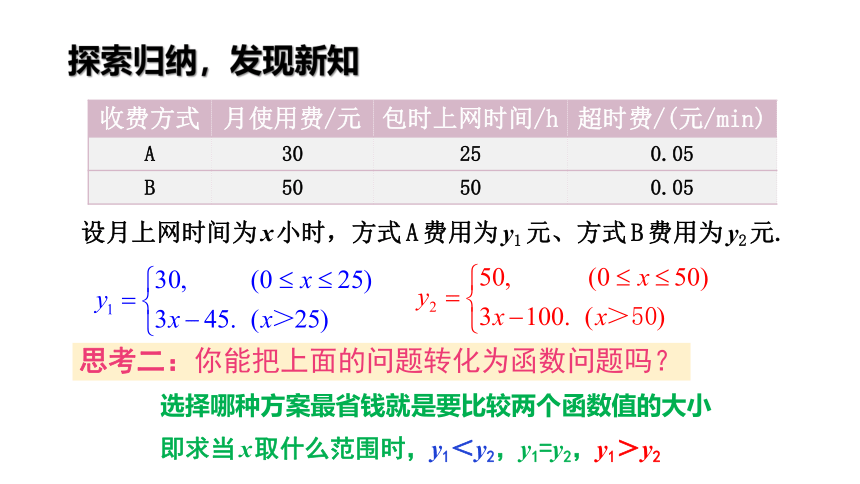
探索归纳,发现新知
问题 怎样选取上网收费方式?
选取哪种方式能节省上网费?
下表给出A,B两种上宽带网的收费方式.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
思考一:选择哪种上网方式的依据是什么?
根据省钱原则(相同时间,用钱最少)选择方案
探索归纳,发现新知
设月上网时间为 x 小时,方式 A 费用为 y1 元、方式 B 费用为 y2 元.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
思考二:你能把上面的问题转化为函数问题吗?
即求当 x 取什么范围时,y1<y2,y1=y2,y1>y2
选择哪种方案最省钱就是要比较两个函数值的大小
探索归纳,发现新知
收费方式A
收费方式B
①当0≤ x ≤25时,
②当25< x ≤50时,
③当x>50时,
选择方式A
要比较 3x-45与 50 的大小,才能决定选择A还是B
选择方式B
y1<y2
y1>y2
(1)当上网时间__________时,选择方式A更省钱.
(2)当上网时间__________时,选择方式B更省钱.
代数方法
仅由函数解析式分析
数形结合
借助函数图像
收费方式A
收费方式B
探索归纳,发现新知
(3)当上网时间__________时,选择A、B方式一样.
探索归纳,发现新知
收费方式A
收费方式B
你能在同一直角坐标系中画出 y1 ,y2的图象吗?
数形结合
探索归纳,发现新知
收费方式A
收费方式B
当25< x ≤50时,
当上网时间__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间________时,选择A、B费用相同.
数形结合
探索归纳,发现新知
选择上网方式
数
形
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
当上网时间 ________时,选择方式A最省钱.
当上网时间______ 时,选择方式B最省钱.
当上网时间______ 时,选择A、B费用相同.
课堂小结,凝练归纳
在解决方案选择问题时,常常要通过建立函数模型来完成.
1. 模型思想——建立函数关系;
方案选择的步骤:
2. 图形直观——画出函数图象;
3. 数形结合——利用函数图象选择方案.
课后练习 拓展提升
练习 (课本P100第15题) 甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
解:
(1)设甲商场的购物金额为 y甲,乙商场的购物金额为 y乙, 则
y甲=0.8 x,
(1)以x(单位/元)表示商品原价,y(单位/元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;
当0≤ x≤ 200时,
(2)在同一坐标系中画出(1)中的两个图象;
(3)春节期间如何选择这两家商场去购物更省钱?
y乙= x
当 x> 200时,
y乙=200+0.7(x-200)=0.7x+60
课后练习 拓展提升
(2)
y甲=0.8 x,
(2)在同一坐标系中画出(1)中的两个图象;
O
x
y
400
600
400
200
200
600
y甲
y乙
(3)春节期间如何选择这两家商场去购物更省钱?
(3)由题(2)图知:
当 x >200时,
解得 x = 600
0.8 x = 0.7 x+60
600
当x>600时,y甲>y乙,选择乙超市省钱,
当0<x <600时,y甲<y乙,选择甲超市省钱,
当x=600时,y甲=y乙,在两商场花钱一样多.
课后练习 拓展提升
数形本是相倚依,怎能分作两边飞;
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休。
——华罗庚
19.3 课题学习 选择方案
情境导入,复习回顾
小明报装宽带上网业务,每月的使用费为 30 元,包时上网 25 小时,每月超出包时的部分每分钟收取0.05元的超时费,设月上网时间为 x 小时,收费 y1 元,请你写出 y1 关于x的函数解析式.
当0≤ x ≤25时,y1= 30 ;
当 x>25时,
y1=30 + 0.05×60(x -25)= 3 x -45
费用
月使用费
超时费
=
+
30
超时费
=
超时时间
×
超时使用价格
(x-25)
0.05×60
×
0.05×60
(x-25)
情境导入,复习回顾
小明报装宽带上网业务,每月的使用费为 30 元,包时上网 25 小时,每月超出包时的部分按每分钟收取0.05元的超时费,设月上网时间为 x 小时,收费 y1 元,请你写出 y1 关于x的函数解析式.
当0≤ x ≤25时,y1= 30 ;
当 x>25时,
合起来可写为:
50
50
y2
y2
y1= 3 x -45
情境导入,复习回顾
小明报装宽带上网业务,每月的使用费为 30 元,包时上网 25 小时,每月超出包时的部分按每分钟收取0.05元的超时费,设月上网时间为 x 小时,收费 y1 元,请你写出 y1 关于x的函数解析式.
50
50
y2
y2
当0≤ x ≤50时,y2=50;
当 x>50时,y2=50+0.05×60(x -50)=3x -100.
探索归纳,发现新知
问题 怎样选取上网收费方式?
选取哪种方式能节省上网费?
下表给出A,B两种上宽带网的收费方式.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
思考一:选择哪种上网方式的依据是什么?
根据省钱原则(相同时间,用钱最少)选择方案
探索归纳,发现新知
设月上网时间为 x 小时,方式 A 费用为 y1 元、方式 B 费用为 y2 元.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
思考二:你能把上面的问题转化为函数问题吗?
即求当 x 取什么范围时,y1<y2,y1=y2,y1>y2
选择哪种方案最省钱就是要比较两个函数值的大小
探索归纳,发现新知
收费方式A
收费方式B
①当0≤ x ≤25时,
②当25< x ≤50时,
③当x>50时,
选择方式A
要比较 3x-45与 50 的大小,才能决定选择A还是B
选择方式B
y1<y2
y1>y2
(1)当上网时间__________时,选择方式A更省钱.
(2)当上网时间__________时,选择方式B更省钱.
代数方法
仅由函数解析式分析
数形结合
借助函数图像
收费方式A
收费方式B
探索归纳,发现新知
(3)当上网时间__________时,选择A、B方式一样.
探索归纳,发现新知
收费方式A
收费方式B
你能在同一直角坐标系中画出 y1 ,y2的图象吗?
数形结合
探索归纳,发现新知
收费方式A
收费方式B
当25< x ≤50时,
当上网时间__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间________时,选择A、B费用相同.
数形结合
探索归纳,发现新知
选择上网方式
数
形
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
当上网时间 ________时,选择方式A最省钱.
当上网时间______ 时,选择方式B最省钱.
当上网时间______ 时,选择A、B费用相同.
课堂小结,凝练归纳
在解决方案选择问题时,常常要通过建立函数模型来完成.
1. 模型思想——建立函数关系;
方案选择的步骤:
2. 图形直观——画出函数图象;
3. 数形结合——利用函数图象选择方案.
课后练习 拓展提升
练习 (课本P100第15题) 甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
解:
(1)设甲商场的购物金额为 y甲,乙商场的购物金额为 y乙, 则
y甲=0.8 x,
(1)以x(单位/元)表示商品原价,y(单位/元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;
当0≤ x≤ 200时,
(2)在同一坐标系中画出(1)中的两个图象;
(3)春节期间如何选择这两家商场去购物更省钱?
y乙= x
当 x> 200时,
y乙=200+0.7(x-200)=0.7x+60
课后练习 拓展提升
(2)
y甲=0.8 x,
(2)在同一坐标系中画出(1)中的两个图象;
O
x
y
400
600
400
200
200
600
y甲
y乙
(3)春节期间如何选择这两家商场去购物更省钱?
(3)由题(2)图知:
当 x >200时,
解得 x = 600
0.8 x = 0.7 x+60
600
当x>600时,y甲>y乙,选择乙超市省钱,
当0<x <600时,y甲<y乙,选择甲超市省钱,
当x=600时,y甲=y乙,在两商场花钱一样多.
课后练习 拓展提升
数形本是相倚依,怎能分作两边飞;
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休。
——华罗庚
