人教版八年级下册20.2 数据的波动程度⑴课件 (共18张PPT)
文档属性
| 名称 | 人教版八年级下册20.2 数据的波动程度⑴课件 (共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:32:55 | ||
图片预览






文档简介
上一节我们学均数、中位数、众数这三个刻画数据集中趋势的统计量.
这节课就让我们运用所学的知识,继续来解决一些实际问题吧!
知识回顾
甲
8
9
6
8
10
8
6
9
乙
8
10
8
7
4
9
10
8
某班有甲、乙两名射击运动员,他们某次的射击成绩如下:
若要选择他们去参加射击竞赛,应根据什么来判断做出选择呢?
从他们成绩的集中趋势方面考虑,计算两名选手成绩的平均数、中位数、众数你能作出选择吗?
甲成绩的中位数:8分
乙成绩的中位数:8分
甲成绩的众数:8分
乙成绩的众数:8分
(1)甲的平均数:8分
(2)
(3)
乙的平均数:
8分
甲成绩的极差:10
–
6
=
4分
乙成绩的极差:10
–
4
=
6分
极差受极端值的影响较大,且不能体现每个数据的波动情况,这样的评判公平吗?
有没有一种既能体现每个数据的波动情况,又不受极端值影响太大的统计量呢?
从他们成绩的波动范围方面考虑,计算两队选手成绩的极差你能作出选择吗?
20.2
数据的波动程度⑴
第二十章
数据的分析
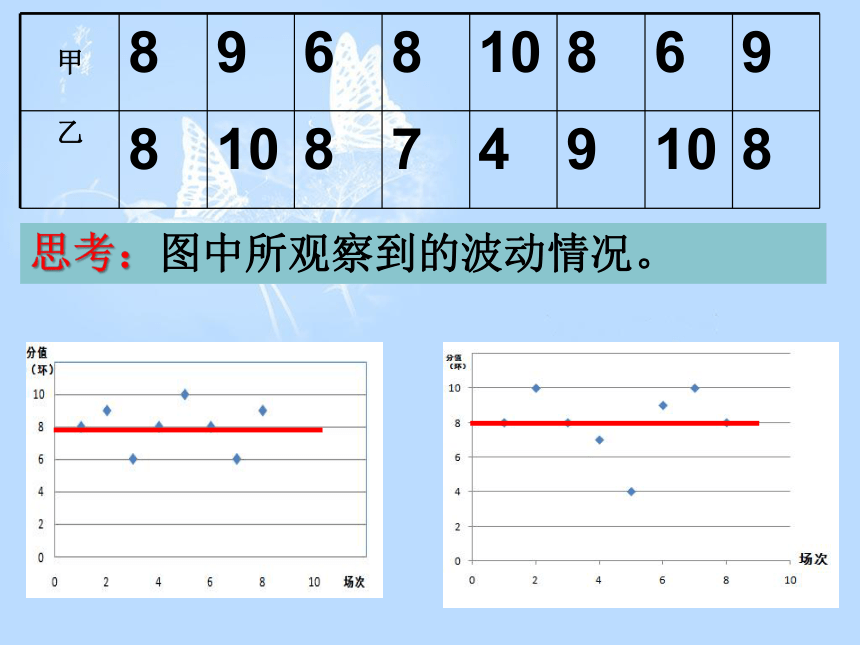
思考:图中所观察到的波动情况。
甲
8
9
6
8
10
8
6
9
乙
8
10
8
7
4
9
10
8
请你评价下列两组数据的波动情况,并用刚才总结的计算方法验证.
A组:
9
1
0
-1
-9
B组:
6
4
0
-4
-6
归纳:
5.若各组数据个数不同,这个计算方法
公平吗?你有解决的方法吗?
波动大
波动小
设有n个数据
x1,x2,…,xn,各数据与它们的平均数的差的平方分别是
,我们用这些值的平均数,即用
来衡量这组数据的波动大小,并把它们叫做这组数据的方差,记作
S2
.
方差的概念:
友情提示:
1、方差是个平均值
2、方差的符号S2本身带有平方
1、在某样本方差的计算公式
中,数字10和8依次表示样本的(
)
A.容量,方差
B.平均数,容量
C.容量,平均数
D.方差,平均数
C
练
习
甲
8
9
6
8
10
8
6
9
乙
8
10
8
7
4
9
10
8
解:甲
=8环
乙
=8环
(请小组分工合作)用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的
.
(1)6
6
6
6
6
6
6
(2)5
5
6
6
6
7
7
(3)3
3
4
6
8
9
9
(4)3
3
3
6
9
9
9
(小组活动)
无波动
波动较小
波动较大
波动最大
数据
由图看波动
平均数
方差
极差
第1组
第2组
第3组
第4组
无波动
波动较小
波动较大
波动最大
6
6
6
6
0
各小组展示数据
观察上表的数据,你知道方差是怎样刻画数据的波动程度吗?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
0
2
6
6
1.如图某班甲、乙两名同学某学期的五次数学测验成绩的折线统计图观察图形,甲、乙这5次数学成绩的方差?
、
哪个大?如下:
2.在某次数学竞赛中,组委会通过计算,得出甲、乙、丙三个学校的学生成绩的方差分别为:
则
学校的学生成绩波动较小.
乙
练
习
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
课堂小结
课后作业
作业:教科书第128页复习巩固第1题.
这节课就让我们运用所学的知识,继续来解决一些实际问题吧!
知识回顾
甲
8
9
6
8
10
8
6
9
乙
8
10
8
7
4
9
10
8
某班有甲、乙两名射击运动员,他们某次的射击成绩如下:
若要选择他们去参加射击竞赛,应根据什么来判断做出选择呢?
从他们成绩的集中趋势方面考虑,计算两名选手成绩的平均数、中位数、众数你能作出选择吗?
甲成绩的中位数:8分
乙成绩的中位数:8分
甲成绩的众数:8分
乙成绩的众数:8分
(1)甲的平均数:8分
(2)
(3)
乙的平均数:
8分
甲成绩的极差:10
–
6
=
4分
乙成绩的极差:10
–
4
=
6分
极差受极端值的影响较大,且不能体现每个数据的波动情况,这样的评判公平吗?
有没有一种既能体现每个数据的波动情况,又不受极端值影响太大的统计量呢?
从他们成绩的波动范围方面考虑,计算两队选手成绩的极差你能作出选择吗?
20.2
数据的波动程度⑴
第二十章
数据的分析
思考:图中所观察到的波动情况。
甲
8
9
6
8
10
8
6
9
乙
8
10
8
7
4
9
10
8
请你评价下列两组数据的波动情况,并用刚才总结的计算方法验证.
A组:
9
1
0
-1
-9
B组:
6
4
0
-4
-6
归纳:
5.若各组数据个数不同,这个计算方法
公平吗?你有解决的方法吗?
波动大
波动小
设有n个数据
x1,x2,…,xn,各数据与它们的平均数的差的平方分别是
,我们用这些值的平均数,即用
来衡量这组数据的波动大小,并把它们叫做这组数据的方差,记作
S2
.
方差的概念:
友情提示:
1、方差是个平均值
2、方差的符号S2本身带有平方
1、在某样本方差的计算公式
中,数字10和8依次表示样本的(
)
A.容量,方差
B.平均数,容量
C.容量,平均数
D.方差,平均数
C
练
习
甲
8
9
6
8
10
8
6
9
乙
8
10
8
7
4
9
10
8
解:甲
=8环
乙
=8环
(请小组分工合作)用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的
.
(1)6
6
6
6
6
6
6
(2)5
5
6
6
6
7
7
(3)3
3
4
6
8
9
9
(4)3
3
3
6
9
9
9
(小组活动)
无波动
波动较小
波动较大
波动最大
数据
由图看波动
平均数
方差
极差
第1组
第2组
第3组
第4组
无波动
波动较小
波动较大
波动最大
6
6
6
6
0
各小组展示数据
观察上表的数据,你知道方差是怎样刻画数据的波动程度吗?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
0
2
6
6
1.如图某班甲、乙两名同学某学期的五次数学测验成绩的折线统计图观察图形,甲、乙这5次数学成绩的方差?
、
哪个大?如下:
2.在某次数学竞赛中,组委会通过计算,得出甲、乙、丙三个学校的学生成绩的方差分别为:
则
学校的学生成绩波动较小.
乙
练
习
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
课堂小结
课后作业
作业:教科书第128页复习巩固第1题.
