人教版八年级下册第十七章第一节勾股定理第一课时教学课件 (共22张PPT)
文档属性
| 名称 | 人教版八年级下册第十七章第一节勾股定理第一课时教学课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:25:27 | ||
图片预览





文档简介
17.1 勾股定理
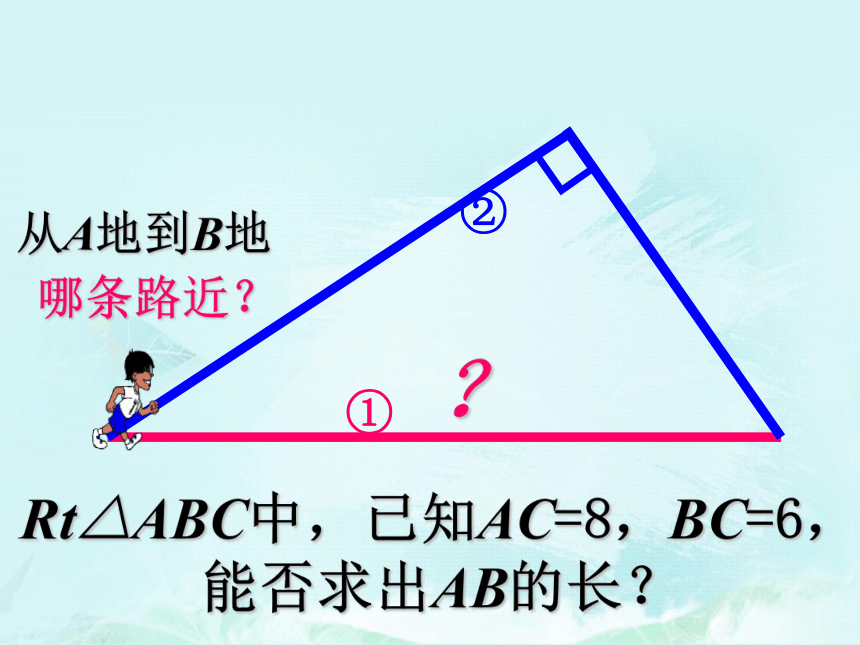
Rt△ABC中,已知AC=8,BC=6,能否求出AB的长?
从A地到B地
哪条路近?
?
②
①
本章我们将探索直角三角形三边之间特有的数量关系,并运用所得结论解决问题
推理论证
获得知识
解决问题
学以致用
观察猜想
实践验证
2500年前,古希腊著名数学家毕达哥拉斯非常善于观察和思考,经常能从平淡的生活现象中发现数学问题.
有一次他在朋友家做客时,发现朋友家用砖铺成的地面中隐藏着深刻的道理
观察:图中两个小正方形与大正方形的面积之间有什么关系?
如果直角三角形两直角边分别为a,b,斜边为c
思考:直角三角形三边之间有什么关系?
a
b
c
C
A
B
a
b
c
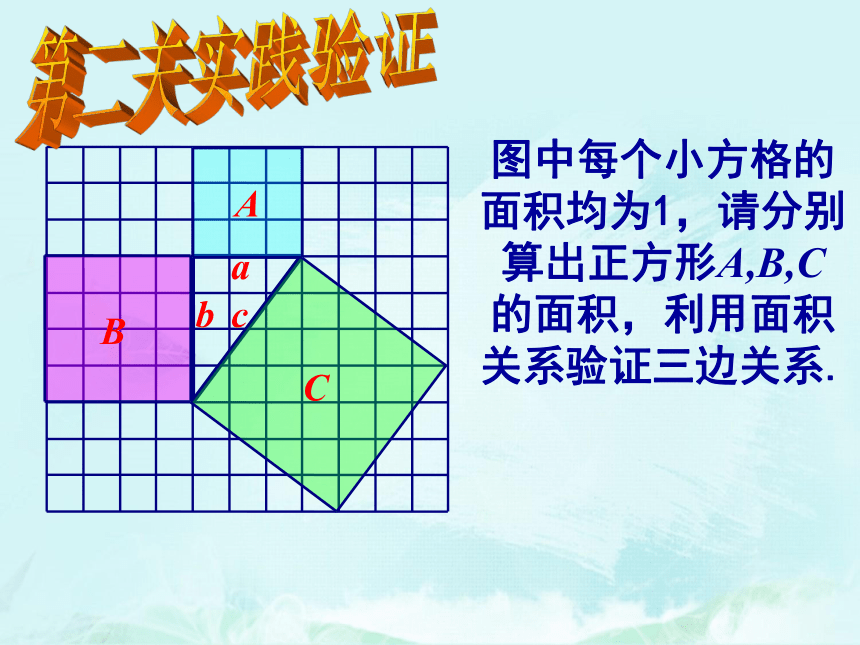
图中每个小方格的面积均为1,请分别算出正方形A,B,C 的面积,利用面积关系验证三边关系.
A
B
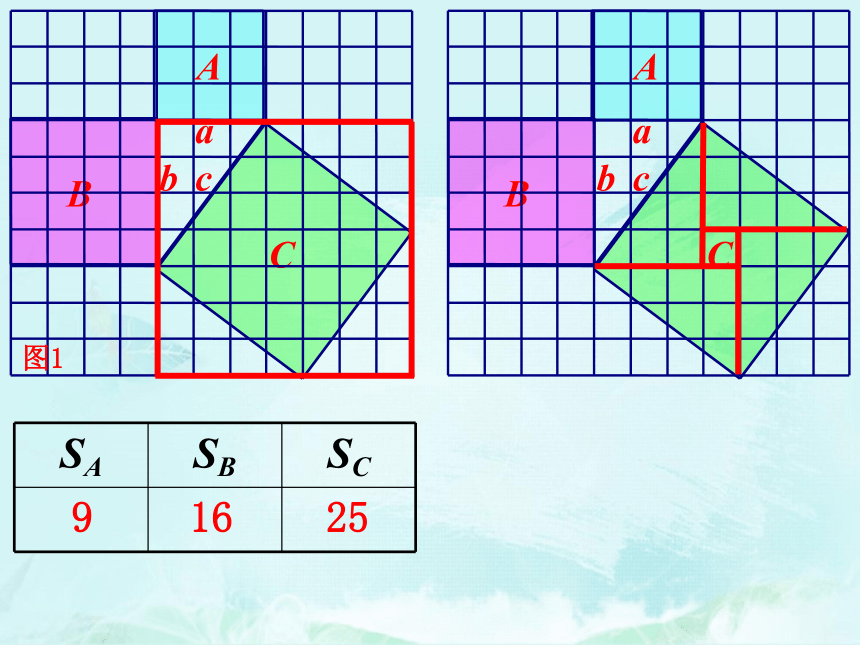
SA
SB
SC
9
16
25
a
b
c
C
A
B
a
b
c
C
图1
A
B
C
图2
A
B
C
图2
SA
SB
SC
4
9
13
a
b
c
用4个全等的直角三角形,拼成一个正方形,利用所拼的正方形的面积证明.
a
b
c
a
b
c
a
b
c
a
b
c
a
A
B
C
┏
b
c
勾
在Rt△ABC中,∵∠C=90° ∴a2 +b2 =c2
直角三角形两直角边的平方和等于斜边的平方.
股
弦
勾股定理
定理:
勾三股四弦五
《周髀算经》中记载:
赵爽弦图
1、Rt△ABC中∠C=90°
若a=5,b=12, 求c
2、Rt△AOB中∠AOB=90°
若AB=2.5,AO=2.4,求BO
┏
a
A
B
C
b
c
学以致用
A
B
O
┏
Rt△ABC中,已知AC=8,BC=6,能否求出AB的长?
?
①
②
解决问题
1m
2m
A
D
C
B
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解决问题
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
2m
A
D
C
B
1m
解:连结AC,在Rt△ABC中, ∠B=90°,根据勾股定理,
>2.2m
答:薄木板能从门框内通过。
AC2 = AB2+BC2= 12+22 =5
∴ AC
┏
试一试
如图,一个2.5m长的梯子AB,斜靠在竖直的墙AO上,AO的距离为2.4m ,
0.4
?
C
D
如果梯子的顶端A沿墙下滑0.4m,
那么梯子的底端B也外移0.4m吗?
2.4
2.5
┏
A
O
B
图中,所有的四边形都是正方形,所有的三角形都是直角三角形,正方形M,N的面积的和是_____.
100
M
N
欣赏美丽的勾股树
A
B
C
D
感受数学之美
100
一种思想
数形结合
一份自豪
身为中国人
勾股定理
一个定理
特殊到一般
一次探索
Rt△ABC中,已知AC=8,BC=6,能否求出AB的长?
从A地到B地
哪条路近?
?
②
①
本章我们将探索直角三角形三边之间特有的数量关系,并运用所得结论解决问题
推理论证
获得知识
解决问题
学以致用
观察猜想
实践验证
2500年前,古希腊著名数学家毕达哥拉斯非常善于观察和思考,经常能从平淡的生活现象中发现数学问题.
有一次他在朋友家做客时,发现朋友家用砖铺成的地面中隐藏着深刻的道理
观察:图中两个小正方形与大正方形的面积之间有什么关系?
如果直角三角形两直角边分别为a,b,斜边为c
思考:直角三角形三边之间有什么关系?
a
b
c
C
A
B
a
b
c
图中每个小方格的面积均为1,请分别算出正方形A,B,C 的面积,利用面积关系验证三边关系.
A
B
SA
SB
SC
9
16
25
a
b
c
C
A
B
a
b
c
C
图1
A
B
C
图2
A
B
C
图2
SA
SB
SC
4
9
13
a
b
c
用4个全等的直角三角形,拼成一个正方形,利用所拼的正方形的面积证明.
a
b
c
a
b
c
a
b
c
a
b
c
a
A
B
C
┏
b
c
勾
在Rt△ABC中,∵∠C=90° ∴a2 +b2 =c2
直角三角形两直角边的平方和等于斜边的平方.
股
弦
勾股定理
定理:
勾三股四弦五
《周髀算经》中记载:
赵爽弦图
1、Rt△ABC中∠C=90°
若a=5,b=12, 求c
2、Rt△AOB中∠AOB=90°
若AB=2.5,AO=2.4,求BO
┏
a
A
B
C
b
c
学以致用
A
B
O
┏
Rt△ABC中,已知AC=8,BC=6,能否求出AB的长?
?
①
②
解决问题
1m
2m
A
D
C
B
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解决问题
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
2m
A
D
C
B
1m
解:连结AC,在Rt△ABC中, ∠B=90°,根据勾股定理,
>2.2m
答:薄木板能从门框内通过。
AC2 = AB2+BC2= 12+22 =5
∴ AC
┏
试一试
如图,一个2.5m长的梯子AB,斜靠在竖直的墙AO上,AO的距离为2.4m ,
0.4
?
C
D
如果梯子的顶端A沿墙下滑0.4m,
那么梯子的底端B也外移0.4m吗?
2.4
2.5
┏
A
O
B
图中,所有的四边形都是正方形,所有的三角形都是直角三角形,正方形M,N的面积的和是_____.
100
M
N
欣赏美丽的勾股树
A
B
C
D
感受数学之美
100
一种思想
数形结合
一份自豪
身为中国人
勾股定理
一个定理
特殊到一般
一次探索
