人教版八年级下册课件19.2.1 正比例函数(共21张PPT)
文档属性
| 名称 | 人教版八年级下册课件19.2.1 正比例函数(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:33:21 | ||
图片预览






文档简介
19.2.1
正比例函数
活动一:情境创设
2019年开始运营的京沪高速铁路全长1
318km.设列车平均速度为300km/h.考虑以下问题:
(1)乘京沪高速列车,从始发站北京南站到终点站海虹桥站,约需要多少小时(结果保留小数点后一位)?
1318÷300≈4.4(h)
活动一:情境创设
(2)京沪高铁列车的行程y(单位:km)与运行时间t(单位:h)之间有何数量关系?
y=300t(0≤t≤4.4)
活动一:情境创设
(3)京沪高铁列车从北京南站出发2.5
h后,是否已经过了距始发站1
100
km的南京南站?
y=300×2.5=750(km),
这时列车尚未
到
达
距
始
发
站
1
100km的南京南站.
写出下列问题中的函数关系式
(2)铁的密度为7.8g/cm3
,铁块的质量m(单位:g)随它的体积v(单位:cm3)大小变化而变化;
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度
h随这些练习本的本数n的变化而变化;
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化.
(2)m=7.8v
(3)h=0.5n
(4)T=-2t
(1)圆的周长
随半径r的大小变化而变化;
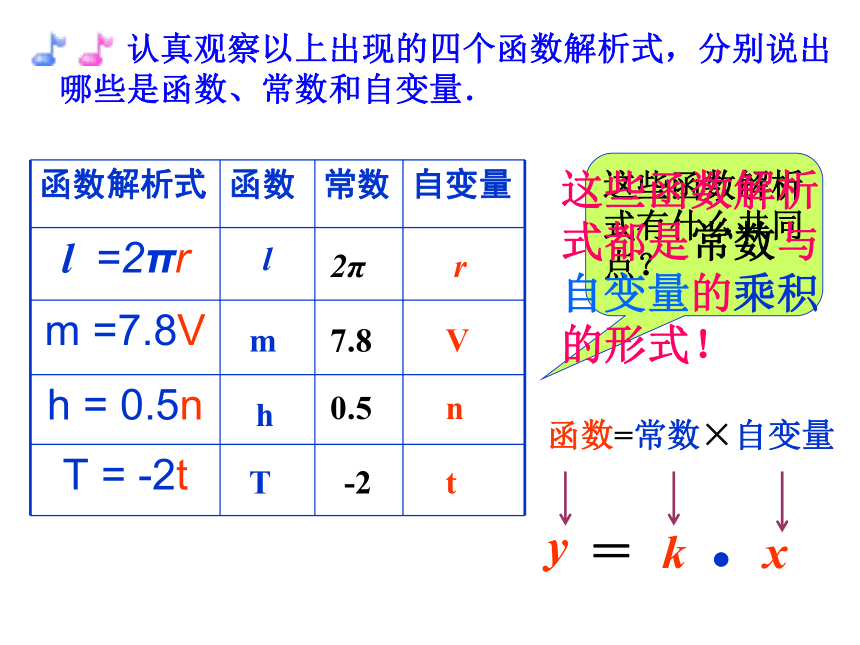
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常数和自变量.
函数解析式
函数
常数
自变量
l
=2πr
m
=7.8V
h
=
0.5n
T
=
-2t
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2π
r
l
7.8
V
m
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
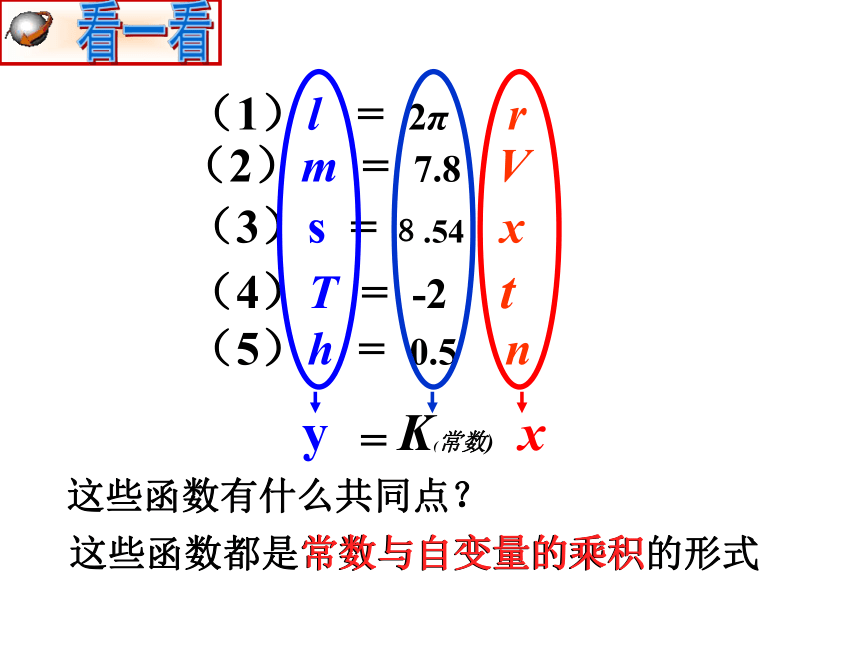
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式
(2)m
=
7.8
V
(5)h
=
0.5
n
(4)T
=
-2
t
(3)s
=
8.54
x
(1)l
=
2π
r
常数与自变量的乘积
y
K(常数)
x
=
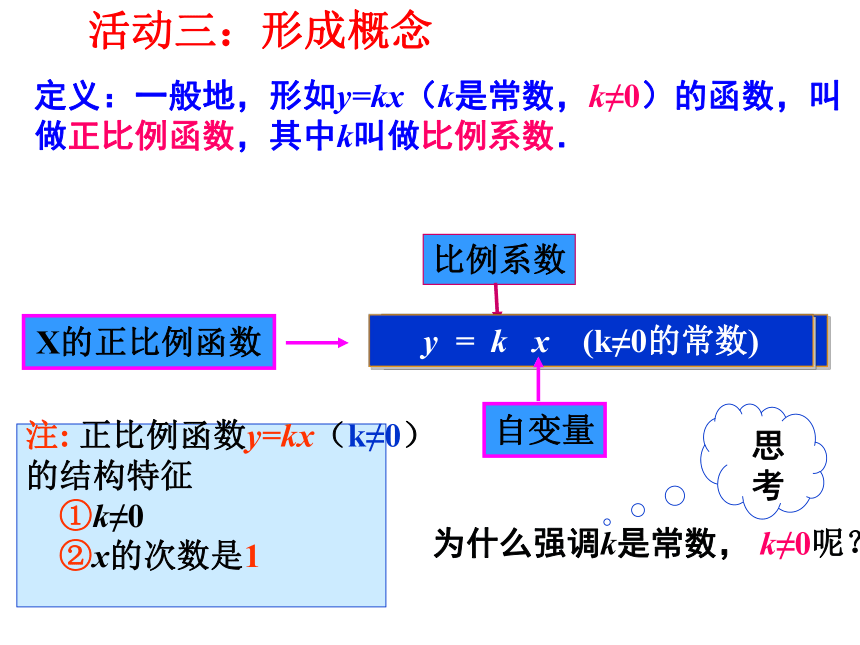
定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
比例系数
X的正比例函数
y
=
k
x
(k≠0的常数)
y
=
k
x
(k≠0的常数)
自变量
注:
正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
为什么强调k是常数,
k≠0呢?
思考
活动三:形成概念
例.下列式子,哪些表示y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x
(2)
(3)y=2x2
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2
)+2x2
是正比例函数,
正比例系数为-0.1
是正比例函数,
正比例系数为0.5
不是正比例函数
不是正比例函数
不是正比例函数
是正比例函数,正比例系数为2
判定一个函数是否是正比例函数,要从化简后来判断!
活动四、辨析概念
下列函数是否是正比例函数?如果是,比例系数是多少?
是,比例系数k=3.
不是.
是,比例系数k=
.
S
不是r的正比例函数,
S是
的正比例函数.
你能举出一些正比例函数的例子吗?
活动五:判定正误
下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数(
)
(2)若y=2x2,则y是x的正比例函数(
)
(3)若y=2(x-1)+2,则y是x的正比例函数(
)
(4)若y=2(x-1)
,则y是x-1的正比例函数(
)
×
×
√
在特定条件下自变量可能不单独就是x了,要注意自变量的变化
√
活动五:判定正误
应用举例·
例
1
已知△ABC的底边BC=8cm,当BC边上的高线从小到大变化时,△ABC的面积也随之变化。
(1)写出△ABC的面积
y(cm2)与高
x
的函数解析式,并指明它是什么函数;
(2)当x=7时,求出
y
的值。
解:(1)
(2)当x=7时,y=4×7=28
它是正比例函数
例2
(1)若y=5x3m-2是正比例函数,则m=
。
(2)若
是正比例函数,则m=
。
1
-2
当m取什么数时,下列函数是正比例函数?
⑴
y=(m-2)x
⑵
y=mx+x
⑶
y=(m2+1)x
活动六、理解概念
(1)若函数
是y关
于x的正比例函数,则m=
(2)若
是正比例
函数,则
m
=
(3)已知函数y=(k-2)x
当k为
何值时,它表示正比例函数?
-1
2
(4).如果y=(k-1)x,是y关于x的正比例函数,则k满足________________.
(5).如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(6).如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
k≠1
2
4
-1
7、若函数y=
-2xm+2是正比例函数,则m的值是
.
8、已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式是______
_____.
9、函数
中自变量x的取值范围是___________.
10、若y=7x+2-3b是正比例函数,则b的值是___________.
11、点A(1,m)在函数y=2x的图象上,则m的值是___________.
12、形如_______
____的函数是正比例函数.
y=-2x
x≥5
b=2/3
2
y=kx
(k≠0)
例3
已知y与x-1成正比例,x
=
8时,y
=6,写出y与x之间函数关系式,并分别求出x
=
4和x
=-3时y的值。
解:∵
y与x-1成正比例
∴设y=k(x-1)
∵
当x=8时,y=6
∴6=7k
∴
∴
y与x之间函数关系式是:y=
(x-1)
当x=4时,y=
×(4-1)=
当x=-3时,y=
×(-3-1)=
活动七、运用概念
巩固练习
把x=1时,y=
-6代入y
=kx+2中,
1、已知y
-2与x成正比,且当x=1时,y=
-6
(1)求y与x之间的函数关系式
(2)若点(a,2)在这个函数图象上,求a
解得k=-8
所以y与x之间的函数关系式
是:y=-8x+2
(2)把点(a,2)
代入y=-8x+2中得:
2=-8a+2
解得a=0
解:
(1)设y
-2=kx,则y=kx+2
2、已知y与x成正比例,且x=2时,y=-6,则当x=9时,求y的值.
解:由题意设函数的解析式:y=kx(k≠0)
所以,-6
=
2k
解得:k
=
-3
因此,该函数的解析式为:y=-3x
当x=9时,y=-3×9=-27
活动八:课堂小结与作业布置
你如何理解正比例函数的意义?能从哪几个方面去认识正比例函数?
1.从语言描述看:
函数关系式是常量与自变量的乘积.
2.从外形特征看:
(1)一般情况下y=kx(常数k≠0);
(2)在特定条件下自变量可能不单独是x了,要注意问题中自变量的变化.
3.从结果形式看:
函数表达式要化简后才能确认为正比例函数
活动八:课堂小结与作业布置
4.从函数关系看:
比例系数k一确定,正比例函数就确定;必须知道两个变量x、y的一对对应值即可确定k.
5.从方程角度看:
如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量.
正比例函数
活动一:情境创设
2019年开始运营的京沪高速铁路全长1
318km.设列车平均速度为300km/h.考虑以下问题:
(1)乘京沪高速列车,从始发站北京南站到终点站海虹桥站,约需要多少小时(结果保留小数点后一位)?
1318÷300≈4.4(h)
活动一:情境创设
(2)京沪高铁列车的行程y(单位:km)与运行时间t(单位:h)之间有何数量关系?
y=300t(0≤t≤4.4)
活动一:情境创设
(3)京沪高铁列车从北京南站出发2.5
h后,是否已经过了距始发站1
100
km的南京南站?
y=300×2.5=750(km),
这时列车尚未
到
达
距
始
发
站
1
100km的南京南站.
写出下列问题中的函数关系式
(2)铁的密度为7.8g/cm3
,铁块的质量m(单位:g)随它的体积v(单位:cm3)大小变化而变化;
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度
h随这些练习本的本数n的变化而变化;
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化.
(2)m=7.8v
(3)h=0.5n
(4)T=-2t
(1)圆的周长
随半径r的大小变化而变化;
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常数和自变量.
函数解析式
函数
常数
自变量
l
=2πr
m
=7.8V
h
=
0.5n
T
=
-2t
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2π
r
l
7.8
V
m
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式
(2)m
=
7.8
V
(5)h
=
0.5
n
(4)T
=
-2
t
(3)s
=
8.54
x
(1)l
=
2π
r
常数与自变量的乘积
y
K(常数)
x
=
定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
比例系数
X的正比例函数
y
=
k
x
(k≠0的常数)
y
=
k
x
(k≠0的常数)
自变量
注:
正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
为什么强调k是常数,
k≠0呢?
思考
活动三:形成概念
例.下列式子,哪些表示y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x
(2)
(3)y=2x2
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2
)+2x2
是正比例函数,
正比例系数为-0.1
是正比例函数,
正比例系数为0.5
不是正比例函数
不是正比例函数
不是正比例函数
是正比例函数,正比例系数为2
判定一个函数是否是正比例函数,要从化简后来判断!
活动四、辨析概念
下列函数是否是正比例函数?如果是,比例系数是多少?
是,比例系数k=3.
不是.
是,比例系数k=
.
S
不是r的正比例函数,
S是
的正比例函数.
你能举出一些正比例函数的例子吗?
活动五:判定正误
下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数(
)
(2)若y=2x2,则y是x的正比例函数(
)
(3)若y=2(x-1)+2,则y是x的正比例函数(
)
(4)若y=2(x-1)
,则y是x-1的正比例函数(
)
×
×
√
在特定条件下自变量可能不单独就是x了,要注意自变量的变化
√
活动五:判定正误
应用举例·
例
1
已知△ABC的底边BC=8cm,当BC边上的高线从小到大变化时,△ABC的面积也随之变化。
(1)写出△ABC的面积
y(cm2)与高
x
的函数解析式,并指明它是什么函数;
(2)当x=7时,求出
y
的值。
解:(1)
(2)当x=7时,y=4×7=28
它是正比例函数
例2
(1)若y=5x3m-2是正比例函数,则m=
。
(2)若
是正比例函数,则m=
。
1
-2
当m取什么数时,下列函数是正比例函数?
⑴
y=(m-2)x
⑵
y=mx+x
⑶
y=(m2+1)x
活动六、理解概念
(1)若函数
是y关
于x的正比例函数,则m=
(2)若
是正比例
函数,则
m
=
(3)已知函数y=(k-2)x
当k为
何值时,它表示正比例函数?
-1
2
(4).如果y=(k-1)x,是y关于x的正比例函数,则k满足________________.
(5).如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(6).如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
k≠1
2
4
-1
7、若函数y=
-2xm+2是正比例函数,则m的值是
.
8、已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式是______
_____.
9、函数
中自变量x的取值范围是___________.
10、若y=7x+2-3b是正比例函数,则b的值是___________.
11、点A(1,m)在函数y=2x的图象上,则m的值是___________.
12、形如_______
____的函数是正比例函数.
y=-2x
x≥5
b=2/3
2
y=kx
(k≠0)
例3
已知y与x-1成正比例,x
=
8时,y
=6,写出y与x之间函数关系式,并分别求出x
=
4和x
=-3时y的值。
解:∵
y与x-1成正比例
∴设y=k(x-1)
∵
当x=8时,y=6
∴6=7k
∴
∴
y与x之间函数关系式是:y=
(x-1)
当x=4时,y=
×(4-1)=
当x=-3时,y=
×(-3-1)=
活动七、运用概念
巩固练习
把x=1时,y=
-6代入y
=kx+2中,
1、已知y
-2与x成正比,且当x=1时,y=
-6
(1)求y与x之间的函数关系式
(2)若点(a,2)在这个函数图象上,求a
解得k=-8
所以y与x之间的函数关系式
是:y=-8x+2
(2)把点(a,2)
代入y=-8x+2中得:
2=-8a+2
解得a=0
解:
(1)设y
-2=kx,则y=kx+2
2、已知y与x成正比例,且x=2时,y=-6,则当x=9时,求y的值.
解:由题意设函数的解析式:y=kx(k≠0)
所以,-6
=
2k
解得:k
=
-3
因此,该函数的解析式为:y=-3x
当x=9时,y=-3×9=-27
活动八:课堂小结与作业布置
你如何理解正比例函数的意义?能从哪几个方面去认识正比例函数?
1.从语言描述看:
函数关系式是常量与自变量的乘积.
2.从外形特征看:
(1)一般情况下y=kx(常数k≠0);
(2)在特定条件下自变量可能不单独是x了,要注意问题中自变量的变化.
3.从结果形式看:
函数表达式要化简后才能确认为正比例函数
活动八:课堂小结与作业布置
4.从函数关系看:
比例系数k一确定,正比例函数就确定;必须知道两个变量x、y的一对对应值即可确定k.
5.从方程角度看:
如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量.
