人教版八年级下册数学 19.1.2函数的图象 第一课时 课件 (共43张PPT)
文档属性
| 名称 | 人教版八年级下册数学 19.1.2函数的图象 第一课时 课件 (共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览




文档简介
第十九章 函数
19.1.2函数的图象
(第一课时)
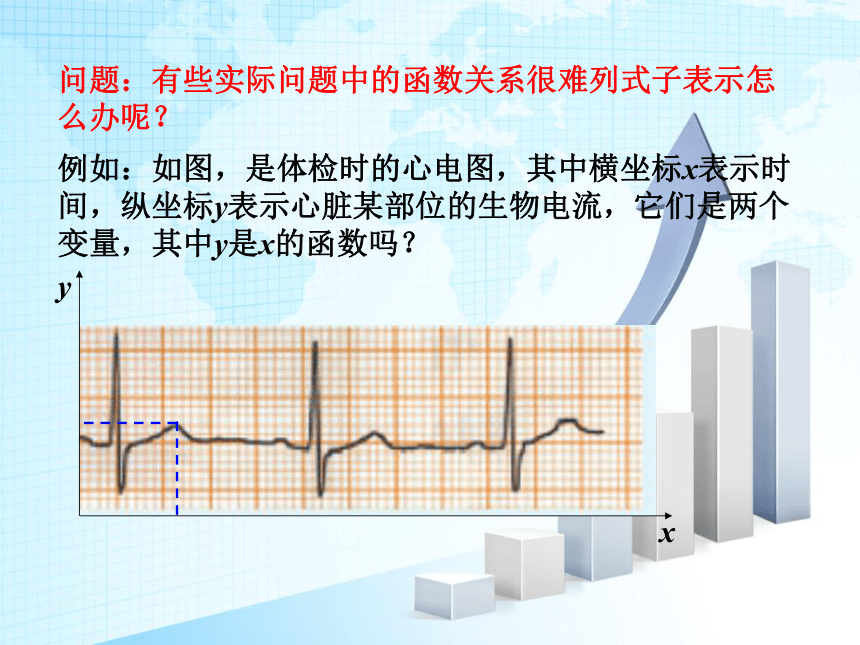
例如:如图,是体检时的心电图,其中横坐标x表示时间,纵坐标y表示心脏某部位的生物电流,它们是两个变量,其中y是x的函数吗?
y
x
问题:有些实际问题中的函数关系很难列式子表示怎
么办呢?
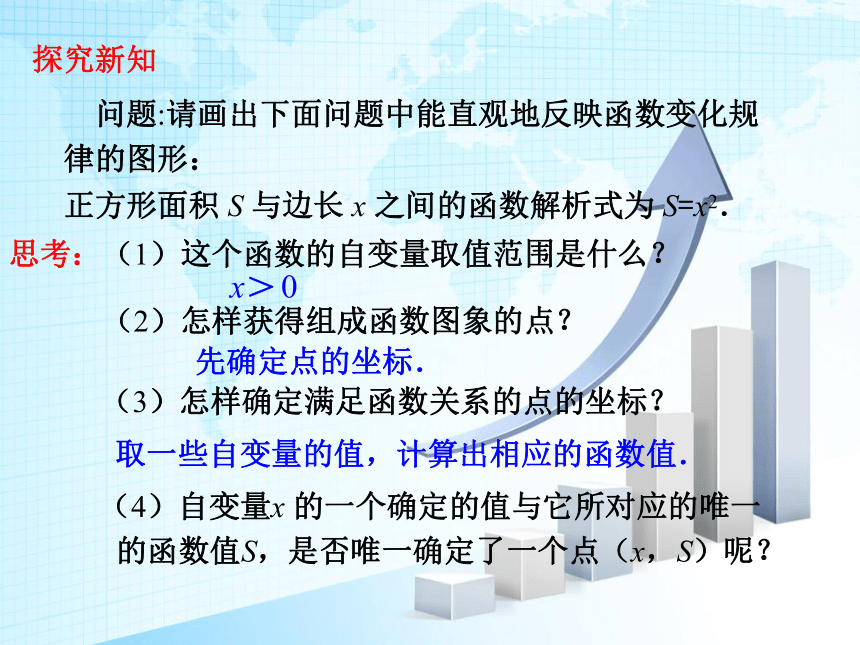
正方形面积 S 与边长 x 之间的函数解析式为 S=x2.
思考:(1)这个函数的自变量取值范围是什么?
(2)怎样获得组成函数图象的点?
先确定点的坐标.
探究新知
问题:请画出下面问题中能直观地反映函数变化规
律的图形:
>
(4)自变量x 的一个确定的值与它所对应的唯一
的函数值S,是否唯一确定了一个点(x,S)呢?
取一些自变量的值,计算出相应的函数值.
(3)怎样确定满足函数关系的点的坐标?
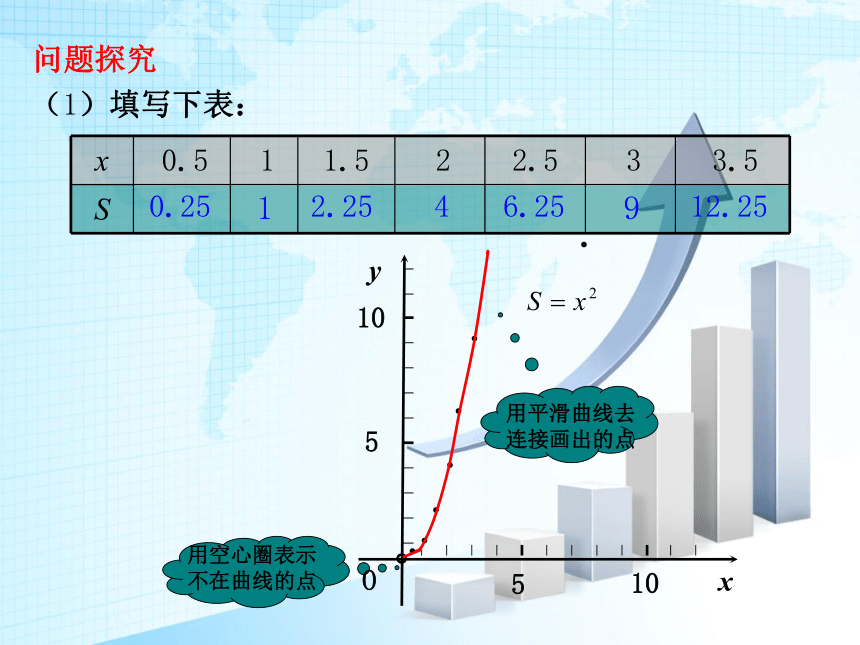
(1)填写下表:
x
0.5
1
1.5
2
2.5
3
3.5
S
0.25
1
2.25
4
6.25
9
12.25
问题探究
用空心圈表示
不在曲线的点
用平滑曲线去
连接画出的点
5
10
O
x
5
10
y
.
.
.
.
.
.
.
。
1.函数图象上任意一点(x,y)中的x,y都满足解析式,
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.如上图中
的曲线就叫函数 S=x2 (x>0)的图象.
什么叫函数图象
2.满足函数解析式的任意一对(x,y)的值所对应的点一定
在函数图象上.
【注意 】
1.列表:在表中列出一些自变量的值及其对应的函数值
画函数图象的步骤:
画函数图象注意的问题:
(1)对于一个函数,把自变量与函数的每一对值分别作为点
的横纵坐标,这样可确定点;
2.描点:在直角坐标系中,以自变量的值为横坐标,对应的
函数值为纵坐标,描出表格中数值对应的各点
3.连线:按横坐标由小到大的顺序,把所描出的各点用平滑
的曲线连接起来
(2)按横坐标由小到大的顺序,把所描出的各点用平滑的曲
线连接起来,不能出现明显的拐弯点
(3)表示x与s的对应关系的点有无数个,实际中只能描出有
限个点,要学会想象出其它点的位置
知识应用
-3
O
4
14
24
8
T/℃
t/时
下图是自动测温仪记录的图象,它反映了北京的春季某天气温T 如何随时间t 的变化而变化.你从图象中得到了哪些信息?
思考:
(1)这天最高气温,最低气温分别是多少?温差是多少?
(2)什么时间段气温上升?什么时间段气温不断下降?
(3)气温的变化规律是什么?
这一天14时气温最高(8℃),凌晨4时气温最低(-3℃),
温差为11℃.
从0时至4时气温呈下降状态(即温度随时间的增加而下降),
从4时到14时气温呈上升状态,从14时至24时气温呈下降状态.
凌晨4时气温最低,中午14时气温最高;从0时至4时气温呈
下降状态(即温度随时间的增加而下降),从4时到14时气温
呈上升状态,从14时至24时气温呈下降状态.
知识应用
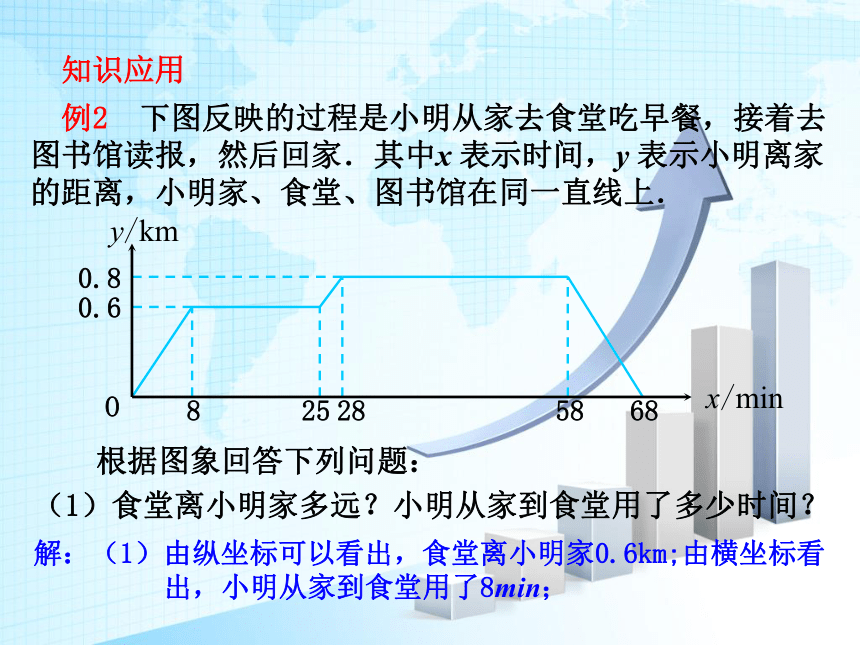
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
解:(1)由纵坐标可以看出,食堂离小明家0.6km;由横坐标看
出,小明从家到食堂用了8min;
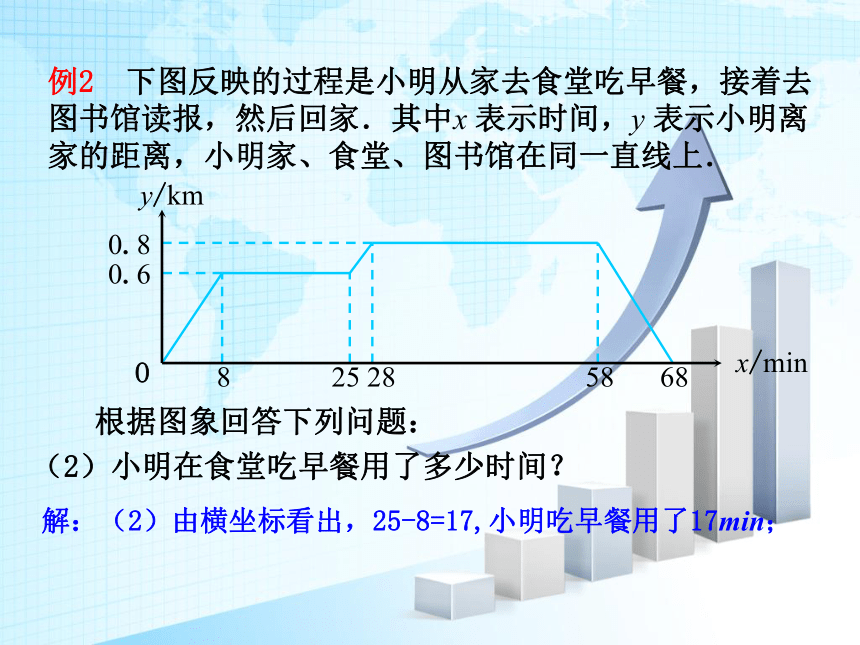
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
根据图象回答下列问题:
(2)小明在食堂吃早餐用了多少时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:(2)由横坐标看出,25-8=17,小明吃早餐用了17min;
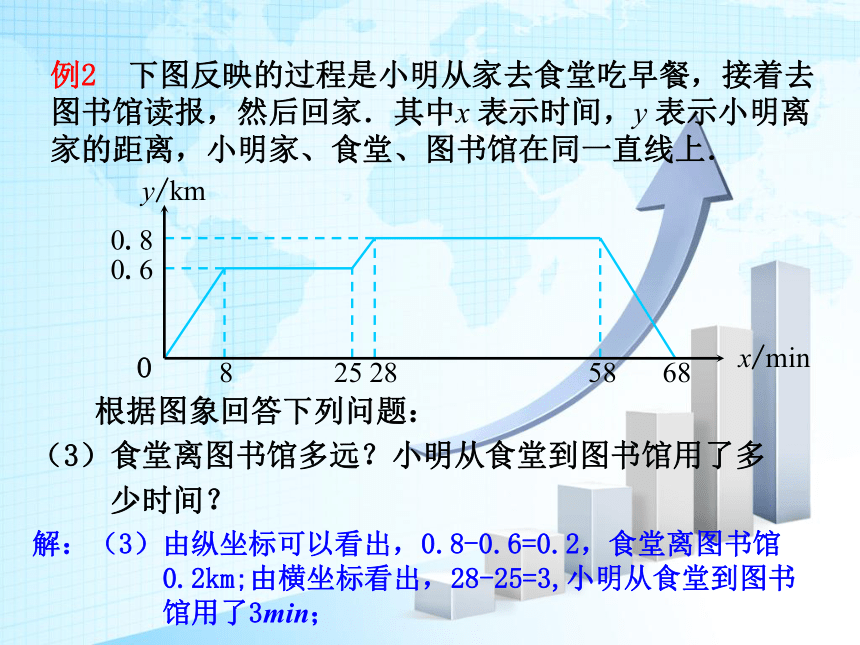
根据图象回答下列问题:
(3)食堂离图书馆多远?小明从食堂到图书馆用了多
少时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
解:(3)由纵坐标可以看出,0.8-0.6=0.2,食堂离图书馆
0.2km;由横坐标看出,28-25=3,小明从食堂到图书
馆用了3min;
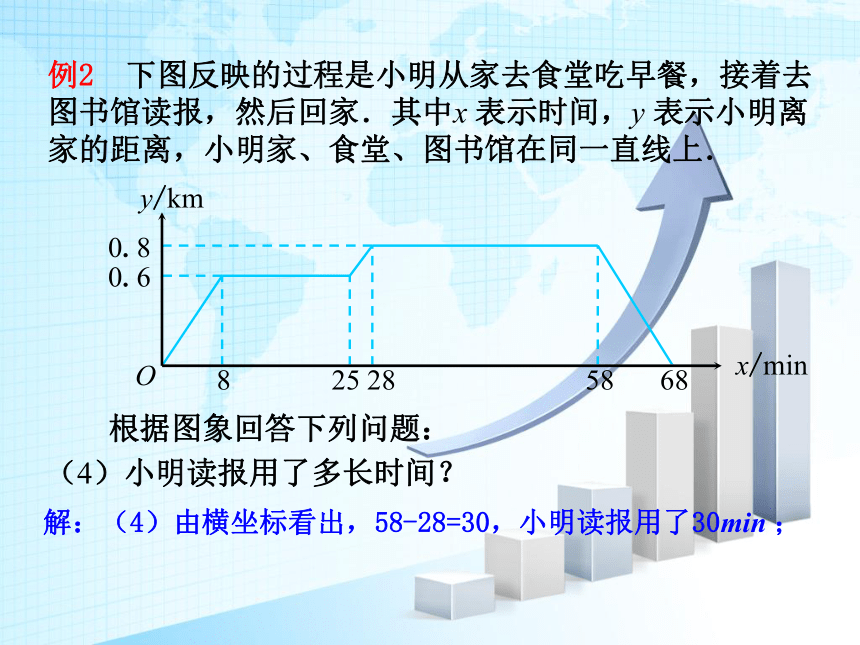
根据图象回答下列问题:
(4)小明读报用了多长时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
解:(4)由横坐标看出,58-28=30,小明读报用了30min ;
根据图象回答下列问题:
(5)图书馆离小明家多远?小明从图书馆回家的平均
速度是多少?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
解:(5)由纵坐标可以看出,图书馆离小明家0.8km;由横坐标
看出,68-58=10,小明从图书馆回家用了10min,由此算
出平均速度是0.08km/min.
(1)本题的图象是由5条线段组成的,它对应5个时间段内的活
动,x表示时间,每条线段左右端点的横坐标之差表示相应
的时间段长,y表示小明离家的距离,每个结论必须弄清楚
其来历;
(2)处理函数图象问题时,首先要注意图象的横纵坐标代表的
意义;其次注意观察单个图象的线性特点①一看升降:距
离与时间的函数图象问题中,图象自左向右上升,说明运
动对象离参照物越来越远;图象自左向右下降,说明运动
对象离参照物地点的距离越来越近;②二看陡缓,图象越
陡,说明运动对象越来越快;图象越平缓,说明运动对象
越来越慢;若是水平线段,说明随时间的流逝而距离不变,
即运动对象停止运动.
【点评】
八年级(1)班从学校出发去某景点旅游,全班分成甲、乙两组.甲组乘坐大客车,乙组乘坐小轿车.已知甲组比乙组先出发,汽车行驶的路程 s(单位:km)和行驶时间 t(单位:min)之间的函数关系如图所示:
跟踪训练
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
给出下列说法:①学校到景点的路程为55 km;②甲组在途中停留了5 min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有 .
①②
拓展:从图象中还能
获得哪些信息?
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
处理函数图象问题时还要注意两个函数图象之间的位置关系
(1)上下关系,如果有两个运动对象,通常会给出两个函
数图象,图象的位置越高表示纵坐标越大,即运动对
象距离照物地点越远;两图象之间的上下间距离越大,
表示两个运动对象的实际距离越远;
(2)交点的意义两个图象的交点表示同一时刻到达相同的
距离,即两个运动对象相遇或有一对象被另一对象追
上.还要注意这个公共点前后的图象变化趋势,一般用
平行于纵轴的直线切函数图象,切点越高的该对象变化
快,否则变化速度慢.
1.如图,是张老师出门散步时离家的距离y与时间x之间的函数
关系的图象,若用黑点表示张老师家的位置,则张老师散步
行走的路线可能是( )
练一练
D
2.如图,水以恒速(即单位时间内注入水的体积相同)注入下面
四种底面积相同的容器中,
(1)请分别找出与各容器对应的水的高度h和时间t的函数关系
图象,用直线段连接起来;
(2)当容器中的水恰好达到一半高度时,请在函数关系图的t
轴上标出此时t值对应点T的位置.
3.如图是我国古代计时器“漏壶”的示意图,在壶内盛一定量
的水,水从壶底的小孔漏出.壶壁内画有刻度,人们根据壶
中水面的位置计时,用x表示时间, y表示壶底到水面的高度,
则y与x的函数关系式的图象是( )
A
C
B
D
【点评】若不考虑水量变化对压力的影响,选 B
若考虑水量变化对压力的影响,选C.
4.一天晚饭后,小明陪妈妈从家里出去散步,下图描述了他们散步过程中离家的距离s(米)与散步时间t( 分) 之间的函数关系,下面的描述符合他们散步情景的是( )
A.从家出发,到了一家书店,看了一会儿书就回家了
B.从家出发,到了一家书店,看了一会儿书,继续向前走了
一段,然后回家了
C.从家出发,一直散步(没有停留),然后回家了
D.从家出发,散了一会儿步,到了一家书店,看了一会儿书,
继续向前走了一段,18分钟后开始返回.
D
5.在如图所示的三个函数图象中,有两个函数图象能近似地
刻画如下a,b两个情境:
情境a :小芳离开家不久,发现把作业本忘在家里,于是
返回了家里找到了作业本再去学校;
情境b :小芳从家出发,走了一段路程后,为了赶时间,
以更快的速度前进.
(1)情境a , b所对应的函数图象分别是______、______
(填写序号);
(2)请你为剩下的函数图象写出一个适合的情境.
③
①
解(2)情境是小芳离开家不久,休息了一会儿,又走回了家.
6.龟兔赛跑
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已经来不及了,乌龟先到达了终点………现在用S1和S2分别表示乌龟、兔子所走的路程,t为时间,则下列图象中,能够表示S和t之间的函数关系式的是( )
D
A
B
C
D
(1) ;
(2) (x>0).
例 下列式子中,对于x每一个确定的值, y有唯
一的对应值,即y是x的函数,请画出这些函
数的图象.
这个函数的自变量取值范围是什么?为什么表格中
-3 前和3 后还有一栏要写省略号?
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
(1) ;
1.列表
例3 下列式子中,对于x每一个确定的值, y有唯
一的对应值,即y是x的函数,请画出这些函
数的图象.
画出的图象是什么?图象上的点从左向右运动时,这个点是越来越高还是越来越低?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
2.描点
3.连线
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
.
.
.
.
y=x+0.5
当自变量的值越来越大时,对应的函数值怎样变化?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
y=x+0.5
练习
画出函数 的图象.
(x>0)
x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
…
12
6
4
3
2.4
2
1.7
1.5
1.2
1
y
4
1
1
6
5
2
3
0
x
2
3
4
5
6
图象从左到右呈下降趋势函数y随x的增大而减小
指出该函数图象有什么特征?
画函数的图象y=2x-1
①列表
x
…
-2
-1
0
1
2
3
…
y
…
-5
-3
-1
1
3
5
…
②描点
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x-1
③连线
指出该函数图象有什么性质?
函数y随x的增大而_____
函数的图象是_______
1.判断点A(-2.5,4) 、B(1,3) 、C(2.5,4)是否在函数y=2x-1的图象上;
2.点D(17,30)和点E(-8,-17)在函数y=2x-1的图象上吗?为什么?
一条直线
增大
点C
点E
-7
5
图象从左到右呈 趋势
上升
3.已知点F(-3,a)和G(b,9)在函数y=2x-1的图象上,则
a=_____,b=______.
描点法画函数图象的一般步骤 :
第一步:列表.(要考虑自变量的取值范围,合理的选择具有代表性的自变量的取值和函数值的对应值.)
第二步:描点.(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表中对应各点.)
第三步:连线.(按照坐标由小到大的顺序把所有点用平滑曲线连接起来,要注意图象的发展趋势.)
归纳:
画函数图象的一般步骤:列表、描点、连线,这种
画函数图象的方法称为描点法.
如何判断一点是否在某个函数的图象上?
若一个点在某个函数图象上,那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在.
我们知道,函数图象是以自变量的值和对应的函数
值分别为横、纵坐标的点组成的图形,这样的点有无数
个,那么怎样判断一个点是否在函数图象上?
(1)判断下列各点是否在函数 的图象上?
①(-4,-4.5); ②(4,4.5).
(2)判断下列各点是否在函数 的图象上?
①(2,3);②(4,2).
(x>0)
1.函数图象上点的横坐标和纵坐标分别表示什么?
课堂小结
图象信息(形)
图象上点的坐标特点(数)
对应关系和变化规律
2.画函数图象时,能画出满足函数关系的所有的点吗?
3.你认为观察函数图象时要注意哪些问题?
1.一艘轮船在同一航线上往返于甲、乙两地,已知轮船在静水
中的速度为15km/h,水流速度为5km/h,轮船先从甲地顺水
航行到乙地,在乙地停留一段时间后,又从乙地逆水航行回
到甲地,设轮船从甲地出发后所用时间为t(h),航行的路
程为s(km),则s与t的函数图象大致是( )
A
B
C
D
课后练习
C
2.如图反映的过程是:小强从家去菜地浇水,又去玉米地除
草,然后回家.如果菜地和玉米地的距离为a千米,小强在
玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值
分别为( )
A.1.1,8 B.0.9,3 C.1.1,12 D.0.9,8
D
3.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了
一段时间后继续骑行,按时赶到了学校,下图中描述了他上学
的情景,错误的说法是( )
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
A
4.如图,夜晚,小亮从点A经过路灯C的正下方
沿直线走到点B,他的影长随他与点A之间的距离的变化而变
化,那么表示y与x之间的函数关系的图象大致为( )
A
5.(2010,天门、潜江、仙桃)甲、乙两人以相同路线前往距
离单位10 km的培训中心参加学习.图中l甲,l乙分别表示甲、
乙两人前往目的地所走的路程s(km)随时间t(min)变化的
函数图象.以下说法:
①乙比甲提前12 min到达;
②甲的平均速度为15 km/h;
③乙走了8km后遇到甲;
④乙出发6 min后追上甲.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
B
6.某厂今年前五个月生产某种产品的总产量Q(件)与时间t
(月)的函数图象如图所示,则下列说法正确的是( )
A.1月至3月每月产量逐月增加,4、5两月每月产量逐月减少
B.1月至3月每月产量逐月增加,4、5两月每月产量与3月持平
C.1月至3月每月产量逐月增加,4、5两月停止生产
D.1月至3月每月产量不变,4、5两月停止生产
B
7.某人从A地向B地打长途电话6分钟,按通话时间收费,3分钟以
内收费2.4元,每加1分钟加收1元,则表示电话费y(元)与通
话时间(分)之间的关系的图象如下图所示,正确的是( )
C
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(1)根据图②中提供的信息,求a,b及图②中c的值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度
后y与出发后的运动时间x(秒)的函数关系式;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的 ?
?
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(1)根据图②中提供的信息,求a,b及图②中c的值;
解:(1)当0≤S1≤40,点P在线段AB上,则S1= AD·AP.
?
若 S1=24,有24= ×8AP ∴ AP=6,即a=6s
?
若 S1=40,有40= ×8AP ∴ AP=10,
?
∴ P点运动6s,速度变为(10-6)÷(8-6)=2即 b=2cm/s
∵点P由B→C→D共用了(c-8)s,运动的路程为18cm ,
∴ 2(c-8)=18 即 c=17 s;
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度
后y与出发后的运动时间x(秒)的函数关系式;
解:(2)y与x之间的函数关系为 y=6+2(x-6)
即 y=2x-6 (6≤x≤17)
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的 ?
?
解:(3)设点P出发ts后,△APD的面积是长方形ABCD的 ,
?
①当点P在AB上时, AD·AP= ×80, AP=5,此时t=5
?
?
②当点P在DC上时,由①可知DP=5,则y=23,x=t
于是 23=2t-6,t=14.5
∴ 点P出发后5s或14.5s,△APD的面积是长方形ABCD的 .
19.1.2函数的图象
(第一课时)
例如:如图,是体检时的心电图,其中横坐标x表示时间,纵坐标y表示心脏某部位的生物电流,它们是两个变量,其中y是x的函数吗?
y
x
问题:有些实际问题中的函数关系很难列式子表示怎
么办呢?
正方形面积 S 与边长 x 之间的函数解析式为 S=x2.
思考:(1)这个函数的自变量取值范围是什么?
(2)怎样获得组成函数图象的点?
先确定点的坐标.
探究新知
问题:请画出下面问题中能直观地反映函数变化规
律的图形:
>
(4)自变量x 的一个确定的值与它所对应的唯一
的函数值S,是否唯一确定了一个点(x,S)呢?
取一些自变量的值,计算出相应的函数值.
(3)怎样确定满足函数关系的点的坐标?
(1)填写下表:
x
0.5
1
1.5
2
2.5
3
3.5
S
0.25
1
2.25
4
6.25
9
12.25
问题探究
用空心圈表示
不在曲线的点
用平滑曲线去
连接画出的点
5
10
O
x
5
10
y
.
.
.
.
.
.
.
。
1.函数图象上任意一点(x,y)中的x,y都满足解析式,
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.如上图中
的曲线就叫函数 S=x2 (x>0)的图象.
什么叫函数图象
2.满足函数解析式的任意一对(x,y)的值所对应的点一定
在函数图象上.
【注意 】
1.列表:在表中列出一些自变量的值及其对应的函数值
画函数图象的步骤:
画函数图象注意的问题:
(1)对于一个函数,把自变量与函数的每一对值分别作为点
的横纵坐标,这样可确定点;
2.描点:在直角坐标系中,以自变量的值为横坐标,对应的
函数值为纵坐标,描出表格中数值对应的各点
3.连线:按横坐标由小到大的顺序,把所描出的各点用平滑
的曲线连接起来
(2)按横坐标由小到大的顺序,把所描出的各点用平滑的曲
线连接起来,不能出现明显的拐弯点
(3)表示x与s的对应关系的点有无数个,实际中只能描出有
限个点,要学会想象出其它点的位置
知识应用
-3
O
4
14
24
8
T/℃
t/时
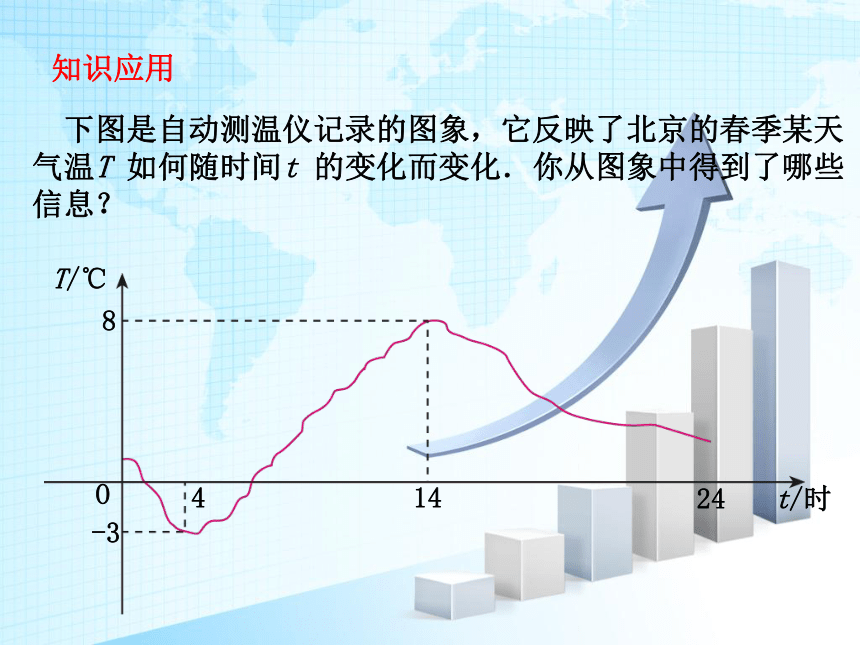
下图是自动测温仪记录的图象,它反映了北京的春季某天气温T 如何随时间t 的变化而变化.你从图象中得到了哪些信息?
思考:
(1)这天最高气温,最低气温分别是多少?温差是多少?
(2)什么时间段气温上升?什么时间段气温不断下降?
(3)气温的变化规律是什么?
这一天14时气温最高(8℃),凌晨4时气温最低(-3℃),
温差为11℃.
从0时至4时气温呈下降状态(即温度随时间的增加而下降),
从4时到14时气温呈上升状态,从14时至24时气温呈下降状态.
凌晨4时气温最低,中午14时气温最高;从0时至4时气温呈
下降状态(即温度随时间的增加而下降),从4时到14时气温
呈上升状态,从14时至24时气温呈下降状态.
知识应用
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
解:(1)由纵坐标可以看出,食堂离小明家0.6km;由横坐标看
出,小明从家到食堂用了8min;
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
根据图象回答下列问题:
(2)小明在食堂吃早餐用了多少时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:(2)由横坐标看出,25-8=17,小明吃早餐用了17min;
根据图象回答下列问题:
(3)食堂离图书馆多远?小明从食堂到图书馆用了多
少时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
解:(3)由纵坐标可以看出,0.8-0.6=0.2,食堂离图书馆
0.2km;由横坐标看出,28-25=3,小明从食堂到图书
馆用了3min;
根据图象回答下列问题:
(4)小明读报用了多长时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
解:(4)由横坐标看出,58-28=30,小明读报用了30min ;
根据图象回答下列问题:
(5)图书馆离小明家多远?小明从图书馆回家的平均
速度是多少?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
例2 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
解:(5)由纵坐标可以看出,图书馆离小明家0.8km;由横坐标
看出,68-58=10,小明从图书馆回家用了10min,由此算
出平均速度是0.08km/min.
(1)本题的图象是由5条线段组成的,它对应5个时间段内的活
动,x表示时间,每条线段左右端点的横坐标之差表示相应
的时间段长,y表示小明离家的距离,每个结论必须弄清楚
其来历;
(2)处理函数图象问题时,首先要注意图象的横纵坐标代表的
意义;其次注意观察单个图象的线性特点①一看升降:距
离与时间的函数图象问题中,图象自左向右上升,说明运
动对象离参照物越来越远;图象自左向右下降,说明运动
对象离参照物地点的距离越来越近;②二看陡缓,图象越
陡,说明运动对象越来越快;图象越平缓,说明运动对象
越来越慢;若是水平线段,说明随时间的流逝而距离不变,
即运动对象停止运动.
【点评】
八年级(1)班从学校出发去某景点旅游,全班分成甲、乙两组.甲组乘坐大客车,乙组乘坐小轿车.已知甲组比乙组先出发,汽车行驶的路程 s(单位:km)和行驶时间 t(单位:min)之间的函数关系如图所示:
跟踪训练
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
给出下列说法:①学校到景点的路程为55 km;②甲组在途中停留了5 min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有 .
①②
拓展:从图象中还能
获得哪些信息?
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
处理函数图象问题时还要注意两个函数图象之间的位置关系
(1)上下关系,如果有两个运动对象,通常会给出两个函
数图象,图象的位置越高表示纵坐标越大,即运动对
象距离照物地点越远;两图象之间的上下间距离越大,
表示两个运动对象的实际距离越远;
(2)交点的意义两个图象的交点表示同一时刻到达相同的
距离,即两个运动对象相遇或有一对象被另一对象追
上.还要注意这个公共点前后的图象变化趋势,一般用
平行于纵轴的直线切函数图象,切点越高的该对象变化
快,否则变化速度慢.
1.如图,是张老师出门散步时离家的距离y与时间x之间的函数
关系的图象,若用黑点表示张老师家的位置,则张老师散步
行走的路线可能是( )
练一练
D
2.如图,水以恒速(即单位时间内注入水的体积相同)注入下面
四种底面积相同的容器中,
(1)请分别找出与各容器对应的水的高度h和时间t的函数关系
图象,用直线段连接起来;
(2)当容器中的水恰好达到一半高度时,请在函数关系图的t
轴上标出此时t值对应点T的位置.
3.如图是我国古代计时器“漏壶”的示意图,在壶内盛一定量
的水,水从壶底的小孔漏出.壶壁内画有刻度,人们根据壶
中水面的位置计时,用x表示时间, y表示壶底到水面的高度,
则y与x的函数关系式的图象是( )
A
C
B
D
【点评】若不考虑水量变化对压力的影响,选 B
若考虑水量变化对压力的影响,选C.
4.一天晚饭后,小明陪妈妈从家里出去散步,下图描述了他们散步过程中离家的距离s(米)与散步时间t( 分) 之间的函数关系,下面的描述符合他们散步情景的是( )
A.从家出发,到了一家书店,看了一会儿书就回家了
B.从家出发,到了一家书店,看了一会儿书,继续向前走了
一段,然后回家了
C.从家出发,一直散步(没有停留),然后回家了
D.从家出发,散了一会儿步,到了一家书店,看了一会儿书,
继续向前走了一段,18分钟后开始返回.
D
5.在如图所示的三个函数图象中,有两个函数图象能近似地
刻画如下a,b两个情境:
情境a :小芳离开家不久,发现把作业本忘在家里,于是
返回了家里找到了作业本再去学校;
情境b :小芳从家出发,走了一段路程后,为了赶时间,
以更快的速度前进.
(1)情境a , b所对应的函数图象分别是______、______
(填写序号);
(2)请你为剩下的函数图象写出一个适合的情境.
③
①
解(2)情境是小芳离开家不久,休息了一会儿,又走回了家.
6.龟兔赛跑
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已经来不及了,乌龟先到达了终点………现在用S1和S2分别表示乌龟、兔子所走的路程,t为时间,则下列图象中,能够表示S和t之间的函数关系式的是( )
D
A
B
C
D
(1) ;
(2) (x>0).
例 下列式子中,对于x每一个确定的值, y有唯
一的对应值,即y是x的函数,请画出这些函
数的图象.
这个函数的自变量取值范围是什么?为什么表格中
-3 前和3 后还有一栏要写省略号?
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
(1) ;
1.列表
例3 下列式子中,对于x每一个确定的值, y有唯
一的对应值,即y是x的函数,请画出这些函
数的图象.
画出的图象是什么?图象上的点从左向右运动时,这个点是越来越高还是越来越低?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
2.描点
3.连线
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
.
.
.
.
y=x+0.5
当自变量的值越来越大时,对应的函数值怎样变化?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
y=x+0.5
练习
画出函数 的图象.
(x>0)
x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
…
12
6
4
3
2.4
2
1.7
1.5
1.2
1
y
4
1
1
6
5
2
3
0
x
2
3
4
5
6
图象从左到右呈下降趋势函数y随x的增大而减小
指出该函数图象有什么特征?
画函数的图象y=2x-1
①列表
x
…
-2
-1
0
1
2
3
…
y
…
-5
-3
-1
1
3
5
…
②描点
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x-1
③连线
指出该函数图象有什么性质?
函数y随x的增大而_____
函数的图象是_______
1.判断点A(-2.5,4) 、B(1,3) 、C(2.5,4)是否在函数y=2x-1的图象上;
2.点D(17,30)和点E(-8,-17)在函数y=2x-1的图象上吗?为什么?
一条直线
增大
点C
点E
-7
5
图象从左到右呈 趋势
上升
3.已知点F(-3,a)和G(b,9)在函数y=2x-1的图象上,则
a=_____,b=______.
描点法画函数图象的一般步骤 :
第一步:列表.(要考虑自变量的取值范围,合理的选择具有代表性的自变量的取值和函数值的对应值.)
第二步:描点.(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表中对应各点.)
第三步:连线.(按照坐标由小到大的顺序把所有点用平滑曲线连接起来,要注意图象的发展趋势.)
归纳:
画函数图象的一般步骤:列表、描点、连线,这种
画函数图象的方法称为描点法.
如何判断一点是否在某个函数的图象上?
若一个点在某个函数图象上,那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在.
我们知道,函数图象是以自变量的值和对应的函数
值分别为横、纵坐标的点组成的图形,这样的点有无数
个,那么怎样判断一个点是否在函数图象上?
(1)判断下列各点是否在函数 的图象上?
①(-4,-4.5); ②(4,4.5).
(2)判断下列各点是否在函数 的图象上?
①(2,3);②(4,2).
(x>0)
1.函数图象上点的横坐标和纵坐标分别表示什么?
课堂小结
图象信息(形)
图象上点的坐标特点(数)
对应关系和变化规律
2.画函数图象时,能画出满足函数关系的所有的点吗?
3.你认为观察函数图象时要注意哪些问题?
1.一艘轮船在同一航线上往返于甲、乙两地,已知轮船在静水
中的速度为15km/h,水流速度为5km/h,轮船先从甲地顺水
航行到乙地,在乙地停留一段时间后,又从乙地逆水航行回
到甲地,设轮船从甲地出发后所用时间为t(h),航行的路
程为s(km),则s与t的函数图象大致是( )
A
B
C
D
课后练习
C
2.如图反映的过程是:小强从家去菜地浇水,又去玉米地除
草,然后回家.如果菜地和玉米地的距离为a千米,小强在
玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值
分别为( )
A.1.1,8 B.0.9,3 C.1.1,12 D.0.9,8
D
3.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了
一段时间后继续骑行,按时赶到了学校,下图中描述了他上学
的情景,错误的说法是( )
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
A
4.如图,夜晚,小亮从点A经过路灯C的正下方
沿直线走到点B,他的影长随他与点A之间的距离的变化而变
化,那么表示y与x之间的函数关系的图象大致为( )
A
5.(2010,天门、潜江、仙桃)甲、乙两人以相同路线前往距
离单位10 km的培训中心参加学习.图中l甲,l乙分别表示甲、
乙两人前往目的地所走的路程s(km)随时间t(min)变化的
函数图象.以下说法:
①乙比甲提前12 min到达;
②甲的平均速度为15 km/h;
③乙走了8km后遇到甲;
④乙出发6 min后追上甲.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
B
6.某厂今年前五个月生产某种产品的总产量Q(件)与时间t
(月)的函数图象如图所示,则下列说法正确的是( )
A.1月至3月每月产量逐月增加,4、5两月每月产量逐月减少
B.1月至3月每月产量逐月增加,4、5两月每月产量与3月持平
C.1月至3月每月产量逐月增加,4、5两月停止生产
D.1月至3月每月产量不变,4、5两月停止生产
B
7.某人从A地向B地打长途电话6分钟,按通话时间收费,3分钟以
内收费2.4元,每加1分钟加收1元,则表示电话费y(元)与通
话时间(分)之间的关系的图象如下图所示,正确的是( )
C
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(1)根据图②中提供的信息,求a,b及图②中c的值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度
后y与出发后的运动时间x(秒)的函数关系式;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的 ?
?
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(1)根据图②中提供的信息,求a,b及图②中c的值;
解:(1)当0≤S1≤40,点P在线段AB上,则S1= AD·AP.
?
若 S1=24,有24= ×8AP ∴ AP=6,即a=6s
?
若 S1=40,有40= ×8AP ∴ AP=10,
?
∴ P点运动6s,速度变为(10-6)÷(8-6)=2即 b=2cm/s
∵点P由B→C→D共用了(c-8)s,运动的路程为18cm ,
∴ 2(c-8)=18 即 c=17 s;
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度
后y与出发后的运动时间x(秒)的函数关系式;
解:(2)y与x之间的函数关系为 y=6+2(x-6)
即 y=2x-6 (6≤x≤17)
8.如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出
发,沿A→B→C→D路线运动,到D停止;点P的速度为每秒
1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,
△APD的面积S1(cm2)与x(秒)的函数关系图象;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的 ?
?
解:(3)设点P出发ts后,△APD的面积是长方形ABCD的 ,
?
①当点P在AB上时, AD·AP= ×80, AP=5,此时t=5
?
?
②当点P在DC上时,由①可知DP=5,则y=23,x=t
于是 23=2t-6,t=14.5
∴ 点P出发后5s或14.5s,△APD的面积是长方形ABCD的 .
