人教版八年级下册数学 第十七章 勾股定理 复习 (共16张PPT)
文档属性
| 名称 | 人教版八年级下册数学 第十七章 勾股定理 复习 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 475.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:25:01 | ||
图片预览






文档简介
小结与复习
第十七章 勾股定理
学习目标 1、复习本章关于勾股定理的知识点,了解方程思想、转化思想在解题过程中的应用。
2、掌握立体图形中的勾股定理问题,通常转化为平面图形问题来解决。
3、掌握勾股定理中的折叠问题的解题思路。
1.如果直角三角形两直角边分别为a,b,斜边为c,
那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
知识回顾 勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
例1 在△ABC中,已知BD是高,∠B=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,求BD的长.
【解析】这是在直角三角形中已知两边长求高的问题,可用勾股定理先求出第三边再求解.
解:∵∠B=90°,∴b是斜边,
则在Rt△ABC中,由勾股定理,得
又∵S△ABC= b?BD= ac,
考点一 勾股定理及其应用
A
C
B
4
3
D
在直角三角形中,已知两边的长求斜边上的高时,先用勾股定理求出第三边,然后用面积求斜边上的高较为简便.在用勾股定理时,一定要清楚直角所对的边才是斜边,例如在上题中不要受勾股数3,4,5的干扰.
方法总结
1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
针对训练
D
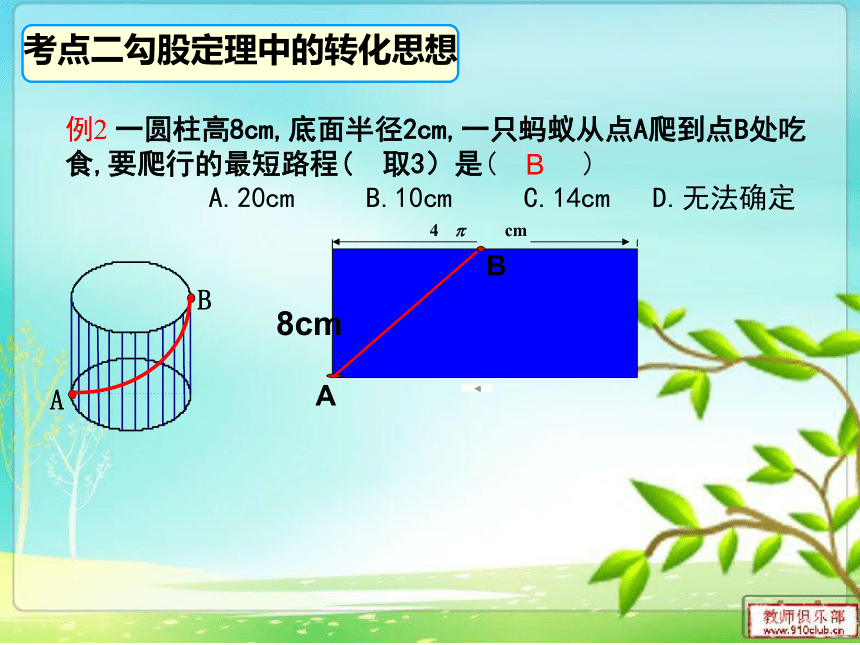
例2 一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( ) A.20cm B.10cm C.14cm D.无法确定
8cm
B
A
B
考点二勾股定理中的转化思想
针对训练
如图所示,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是____
√5
A
B
如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.则这块地
的面积为 .
A
B
C
3
4
13
12
D
针对训练
解析:连接AC.由AD=4m,CD=3m,∠ADC=90°,可得AC=5m.再由AB=13m,BC=12m,可知△ABC是直角三角形.于是这块地的面积为(12×5-3×4)÷2=24(cm2)
24cm2
1、用勾股定理解决立体图形的问题,常以长方体、正方体、圆柱、圆锥为背景,做题思路是“展曲为平” ——把立体图形转化为平面图形,即将原图形的侧面展开转化为平面图形问题,再运用“平面上的两点之间线段最短”求解.
方法总结
2、不规则图形转化成规则图形来解答。
针对训练
例3.如图,小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,请你能帮他算出旗 杆的高为 ( ) 米
考点三勾股定理中的方程思想
在Rt△ABC中,∠C=90°,
若a︰b=3︰4,c=10,
则a= ________ , b=________
6
8
12
方法总结
方法总结
方程思想在勾股定理中的应用很广泛,大体思路是设其中一条边是X,利用勾股定理 列方程、解方程、再求各边的长。
考点四 勾股定理与折叠问题
例4 已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
问题:1.由AB=8,BC=10,你可以知道哪些线段长?
2.在Rt△DFC中,你可以求出DF的长吗?
3.由DF的长,你还可以求出哪条线段长?
4.设BE = x,你可以用含有x的式子表示出哪些线段长?
解:由折叠可知FC=BC=10,BE=FE.
在长方形ABCD中,DC=AB=8 ,
AD=BC=10,∠D=90°.
∴DF=6, AF=4.
设BE=FE=x,则AE=8-x .
在Rt△AFE中,由勾股定理得
∴ ,解得 x = 5 .
∴BE的长为5.
方法总结
方法总结
1、折叠规律是:折叠部分的图形,折叠前后,关于折痕成轴对称,两图形全等。
2、利用线段关系和勾股定理列方程计算。
课堂小结 说说你这节课有哪些收获?
布置作业:
作业:课本复习题17 (1)必做题1、2、5、6、7题 (2)选做题8、9、10任选其二
第十七章 勾股定理
学习目标 1、复习本章关于勾股定理的知识点,了解方程思想、转化思想在解题过程中的应用。
2、掌握立体图形中的勾股定理问题,通常转化为平面图形问题来解决。
3、掌握勾股定理中的折叠问题的解题思路。
1.如果直角三角形两直角边分别为a,b,斜边为c,
那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
知识回顾 勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
例1 在△ABC中,已知BD是高,∠B=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,求BD的长.
【解析】这是在直角三角形中已知两边长求高的问题,可用勾股定理先求出第三边再求解.
解:∵∠B=90°,∴b是斜边,
则在Rt△ABC中,由勾股定理,得
又∵S△ABC= b?BD= ac,
考点一 勾股定理及其应用
A
C
B
4
3
D
在直角三角形中,已知两边的长求斜边上的高时,先用勾股定理求出第三边,然后用面积求斜边上的高较为简便.在用勾股定理时,一定要清楚直角所对的边才是斜边,例如在上题中不要受勾股数3,4,5的干扰.
方法总结
1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
针对训练
D
例2 一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( ) A.20cm B.10cm C.14cm D.无法确定
8cm
B
A
B
考点二勾股定理中的转化思想
针对训练
如图所示,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是____
√5
A
B
如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.则这块地
的面积为 .
A
B
C
3
4
13
12
D
针对训练
解析:连接AC.由AD=4m,CD=3m,∠ADC=90°,可得AC=5m.再由AB=13m,BC=12m,可知△ABC是直角三角形.于是这块地的面积为(12×5-3×4)÷2=24(cm2)
24cm2
1、用勾股定理解决立体图形的问题,常以长方体、正方体、圆柱、圆锥为背景,做题思路是“展曲为平” ——把立体图形转化为平面图形,即将原图形的侧面展开转化为平面图形问题,再运用“平面上的两点之间线段最短”求解.
方法总结
2、不规则图形转化成规则图形来解答。
针对训练
例3.如图,小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,请你能帮他算出旗 杆的高为 ( ) 米
考点三勾股定理中的方程思想
在Rt△ABC中,∠C=90°,
若a︰b=3︰4,c=10,
则a= ________ , b=________
6
8
12
方法总结
方法总结
方程思想在勾股定理中的应用很广泛,大体思路是设其中一条边是X,利用勾股定理 列方程、解方程、再求各边的长。
考点四 勾股定理与折叠问题
例4 已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
问题:1.由AB=8,BC=10,你可以知道哪些线段长?
2.在Rt△DFC中,你可以求出DF的长吗?
3.由DF的长,你还可以求出哪条线段长?
4.设BE = x,你可以用含有x的式子表示出哪些线段长?
解:由折叠可知FC=BC=10,BE=FE.
在长方形ABCD中,DC=AB=8 ,
AD=BC=10,∠D=90°.
∴DF=6, AF=4.
设BE=FE=x,则AE=8-x .
在Rt△AFE中,由勾股定理得
∴ ,解得 x = 5 .
∴BE的长为5.
方法总结
方法总结
1、折叠规律是:折叠部分的图形,折叠前后,关于折痕成轴对称,两图形全等。
2、利用线段关系和勾股定理列方程计算。
课堂小结 说说你这节课有哪些收获?
布置作业:
作业:课本复习题17 (1)必做题1、2、5、6、7题 (2)选做题8、9、10任选其二
