人教版八年级下册数学17.1勾股定理的应用(一)课件(共16张PPT)
文档属性
| 名称 | 人教版八年级下册数学17.1勾股定理的应用(一)课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 471.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:30:17 | ||
图片预览



文档简介
新人教版八年级下册
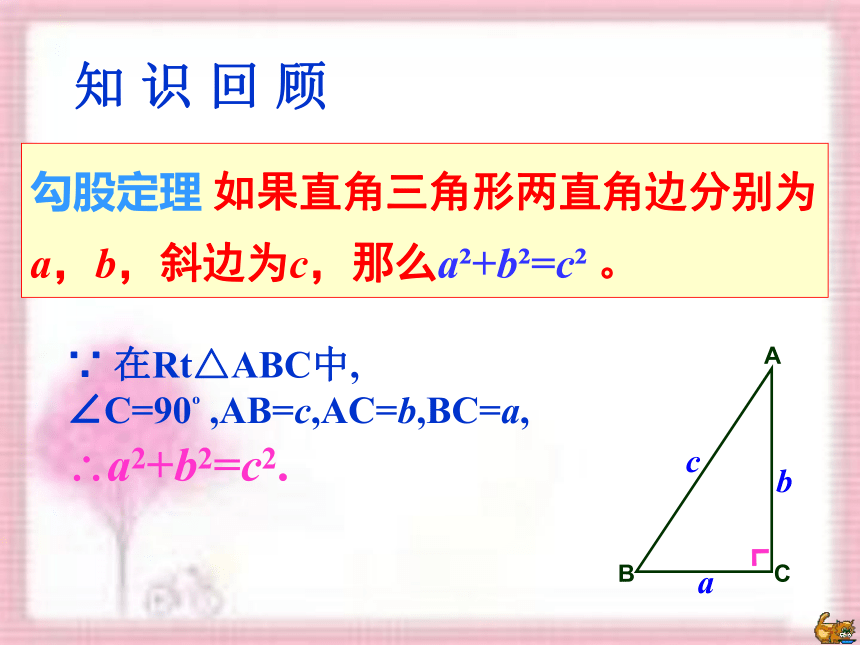
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a?+b?=c? 。
c
a
b
A
B
C
∵ 在Rt△ABC中, ∠C=90? ,AB=c,AC=b,BC=a,
?a2+b2=c2.
┏
知 识 回 顾
1 已知直角三角形ABC的三边为a,b,c , ∠C= 90°,写出 a,b,c 三者之间的关系
2 矩形的一边长是5,对角线是13,则
它的面积是多少?
3、若一个直角三角形两条直角边长 是3和2,那么第三条边长是多少?
4、若一个直角三角形两条边长是3和2,那么第三条边长是多少?
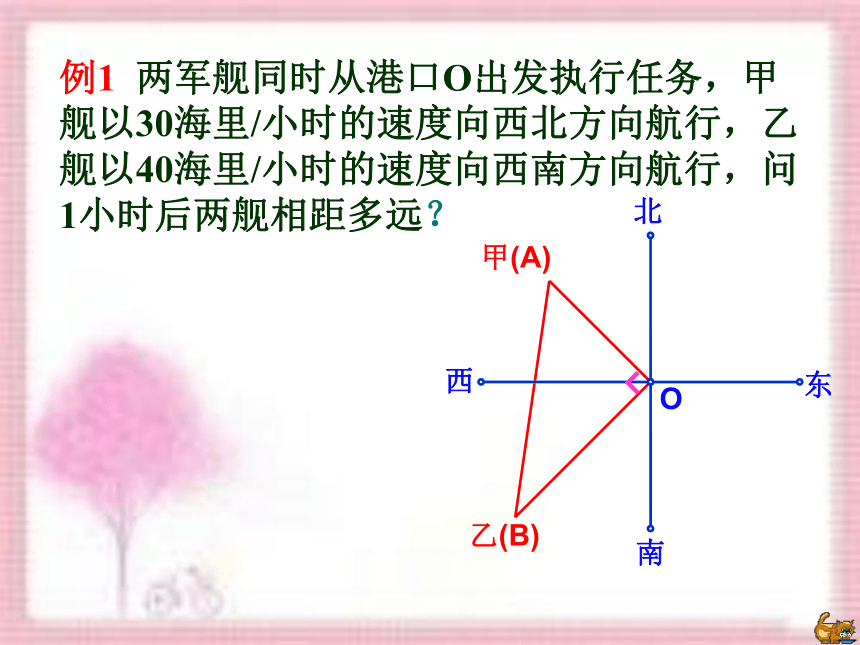
例1 两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?
甲(A)
西
东
北
南
O
乙(B)
┏
A
B
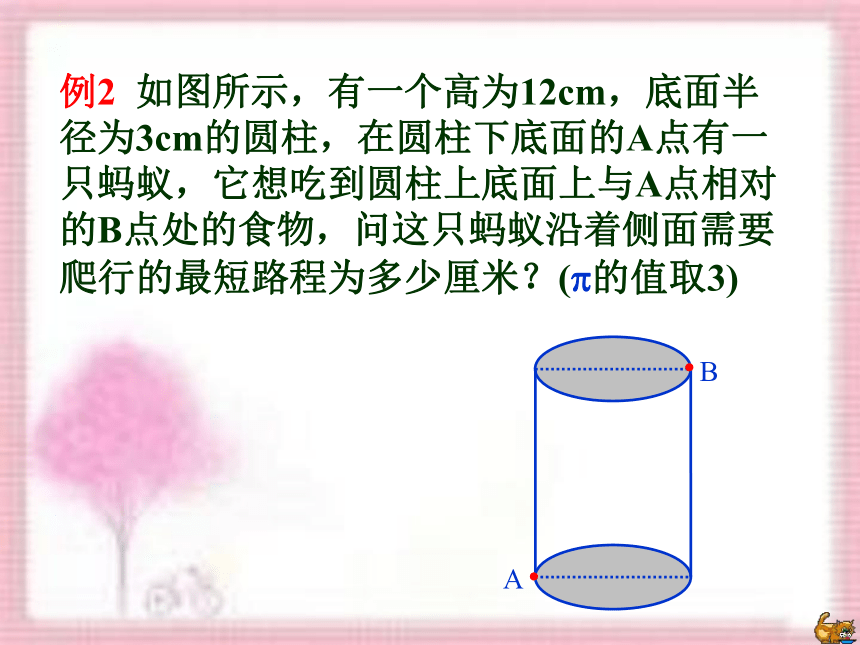
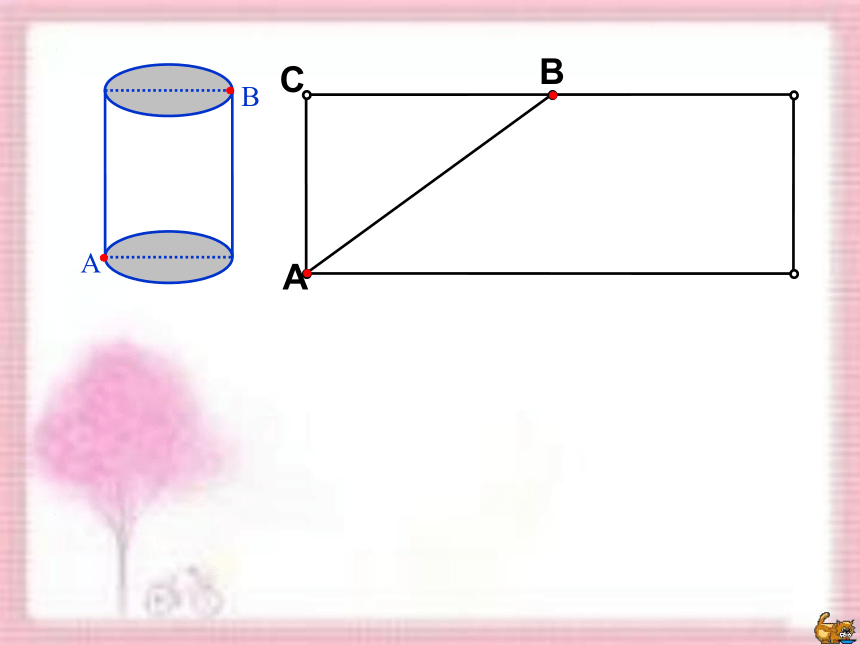
例2 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(?的值取3)
A
C
B
A
B
变式:1如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
A
B
10
10
10
B
C
A
2.如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少?
2
0.3
0.2
A
B
A
B
C
2m
(0.2×3+0.3×3)m
A
B
O
3
2
C
D
例3
如图,一个三米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
O
3
2
D
C
y=0
分析
要求梯子的底端是否滑动0.5m,只需求出BD的长是否为0.5米。
由图可知BD=OD-OB.则需先求出OD,OB的长。
解:在Rt△AOB中
A
B
O
3
2
D
C
所以梯子的顶端下滑0.5m,它的底端不是滑动0.5m.
解:在Rt△COD中,
图(1)
图(2)
A
B
C
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?
问题的延伸
小结:勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,尝试把立体图形转换为平面图形。
学生畅谈本节课收获
恭喜你,认真地听完了这节课!
作 业
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a?+b?=c? 。
c
a
b
A
B
C
∵ 在Rt△ABC中, ∠C=90? ,AB=c,AC=b,BC=a,
?a2+b2=c2.
┏
知 识 回 顾
1 已知直角三角形ABC的三边为a,b,c , ∠C= 90°,写出 a,b,c 三者之间的关系
2 矩形的一边长是5,对角线是13,则
它的面积是多少?
3、若一个直角三角形两条直角边长 是3和2,那么第三条边长是多少?
4、若一个直角三角形两条边长是3和2,那么第三条边长是多少?
例1 两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?
甲(A)
西
东
北
南
O
乙(B)
┏
A
B
例2 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(?的值取3)
A
C
B
A
B
变式:1如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
A
B
10
10
10
B
C
A
2.如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少?
2
0.3
0.2
A
B
A
B
C
2m
(0.2×3+0.3×3)m
A
B
O
3
2
C
D
例3
如图,一个三米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
O
3
2
D
C
y=0
分析
要求梯子的底端是否滑动0.5m,只需求出BD的长是否为0.5米。
由图可知BD=OD-OB.则需先求出OD,OB的长。
解:在Rt△AOB中
A
B
O
3
2
D
C
所以梯子的顶端下滑0.5m,它的底端不是滑动0.5m.
解:在Rt△COD中,
图(1)
图(2)
A
B
C
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?
问题的延伸
小结:勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,尝试把立体图形转换为平面图形。
学生畅谈本节课收获
恭喜你,认真地听完了这节课!
作 业
