人教版八年级下册数学18.1.2平行四边形判定第三课时 (共19张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.2平行四边形判定第三课时 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览



文档简介
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平等四边形
∵AB=CD,AD= BC ∴…是平行四边形
定理2
对角线互相平分的四边形是平行四边形
∵OA=OC,OB=
OD ∴…是平行四边形
推论
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,∠B=∠D
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
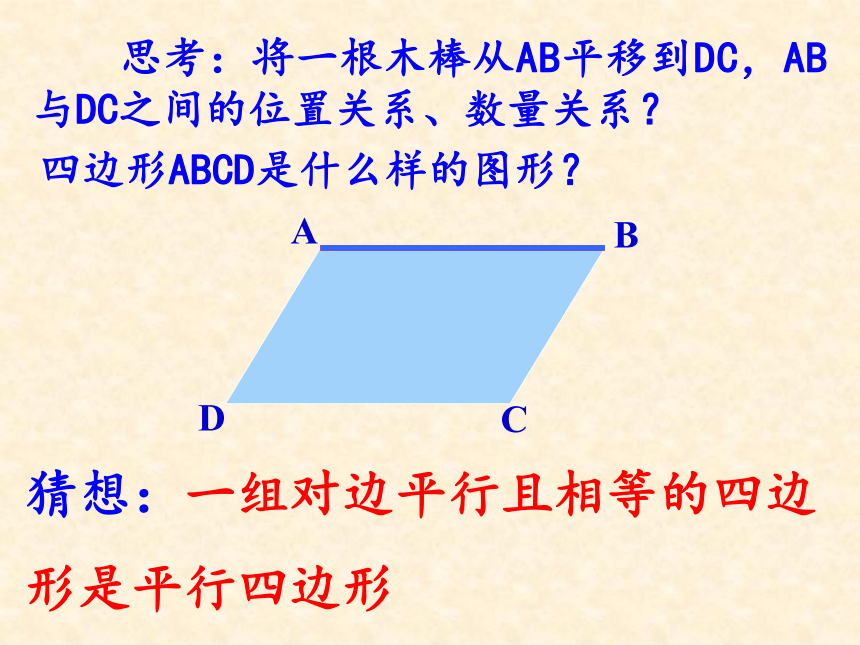
思考:将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?
A
B
C
D
四边形ABCD是什么样的图形?
猜想:一组对边平行且相等的四边
形是平行四边形
A
B
C
D
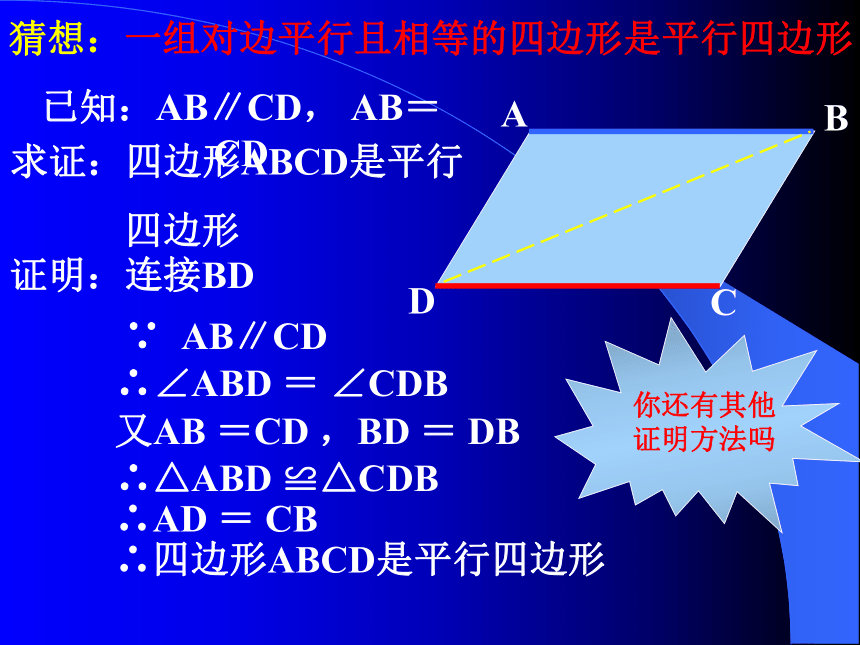
猜想:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行
四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又AB =CD ,BD = DB
∴△ABD ≌△CDB
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
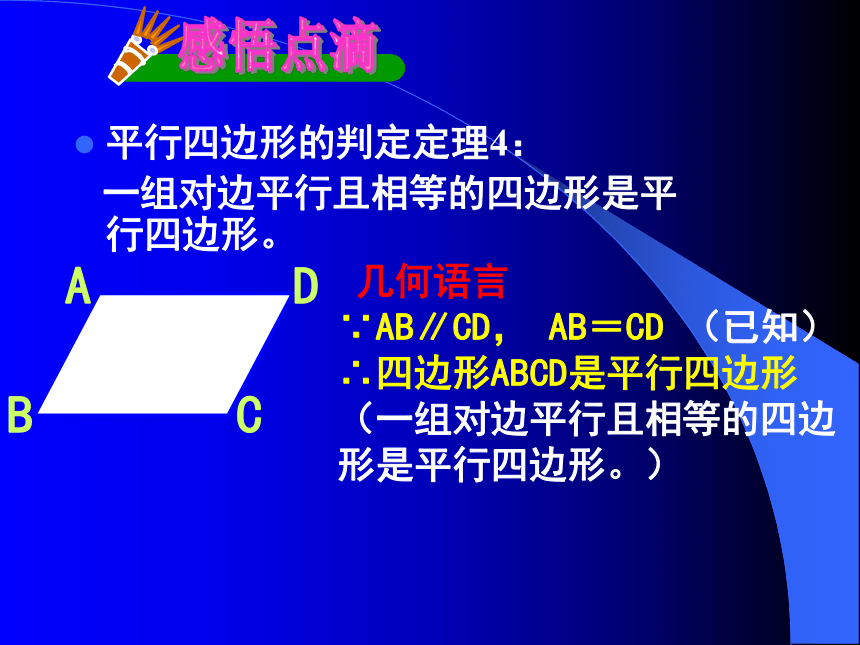
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形。
A
B
C
D
几何语言
∵AB∥CD, AB=CD (已知)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。)
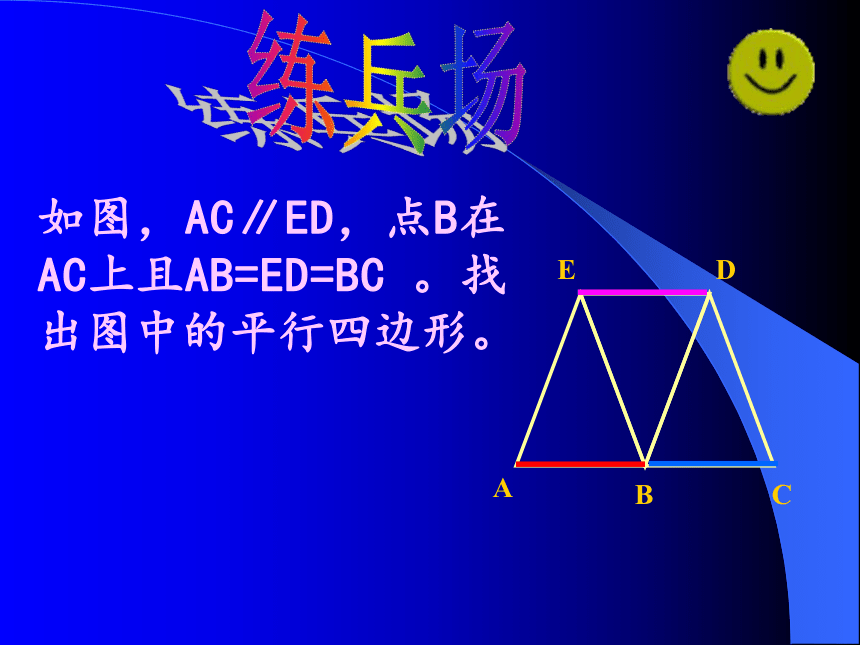
如图,AC∥ED,点B在AC上且AB=ED=BC 。找出图中的平行四边形。
A
C
B
E
D
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
平行四边形的判定方法共有几种?
已知:四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,需添加一个条件是: (只需填一个你认为正确的条件即可)。
A
D
B
C
对于四边形ABCD,如果从条件①AB∥CD;
②AD∥BC;③AB=CD;④BC=AD中选出两个,写出所有能说明四边形ABCD是平行四边形的有 .(填序号)
A
D
B
C
如图, □ABCD中,点E、F分别在AB、CD上且DF=BE 。四边形DEBF是平行四边形吗? 说说理由。
E
B
F
C
D
A
已知:如图,□ABCD中,E、F分别是AD、BC的中点,
求证:BE=DF.
变式练习
A
B
C
D
E
F
已知:如图,E,F是平行四边形ABCD的对角线上的两点,AE=CF.
应用
求证:四边形BEDF是平行四边形.
F
D
A
B
C
E
O
已知:平行四边形ABCD,对角线AC的中点为O,并且E、F分别为OA、OC的中点。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
变式练习
开动脑筋
老师手里有一个平行四边形的玻璃碎片,巧的是刚好从A、C两个顶点断裂。你能用所学的知识帮她补好吗?说说你的想法和理由。
A
B
C
如图,在 ?ABCD中,已知两条对角线相交于点O,E、F、G、H分别是AO、BO、CO、DO的中点,以图中的点为顶点,尽可能多地画出平行四边形。
A
D
C
B
E
F
G
H
O
A
D
C
B
E
F
G
H
O
A
D
C
B
E
F
G
H
O
2、本节课主要运用什么方法来解决一些简单的实际问题?
1、经过本节课的学习,你有哪些收获?
小 结
经过本节课的学习,
你有哪些收获?
请和我们一起分享.
基础题:P49练习第4-6题。
探究题:现有一块等腰直角三角形铁板,要求切割一次焊接成一个含有45°角的平行四边形(不能有余料), 请你设计一种方案,并说明该方案正确的理由.
试金石
A
B
C
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致我亲爱的同学们:
谢谢大家
——毕达哥拉斯
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平等四边形
∵AB=CD,AD= BC ∴…是平行四边形
定理2
对角线互相平分的四边形是平行四边形
∵OA=OC,OB=
OD ∴…是平行四边形
推论
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,∠B=∠D
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
思考:将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?
A
B
C
D
四边形ABCD是什么样的图形?
猜想:一组对边平行且相等的四边
形是平行四边形
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行
四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又AB =CD ,BD = DB
∴△ABD ≌△CDB
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形。
A
B
C
D
几何语言
∵AB∥CD, AB=CD (已知)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。)
如图,AC∥ED,点B在AC上且AB=ED=BC 。找出图中的平行四边形。
A
C
B
E
D
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
平行四边形的判定方法共有几种?
已知:四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,需添加一个条件是: (只需填一个你认为正确的条件即可)。
A
D
B
C
对于四边形ABCD,如果从条件①AB∥CD;
②AD∥BC;③AB=CD;④BC=AD中选出两个,写出所有能说明四边形ABCD是平行四边形的有 .(填序号)
A
D
B
C
如图, □ABCD中,点E、F分别在AB、CD上且DF=BE 。四边形DEBF是平行四边形吗? 说说理由。
E
B
F
C
D
A
已知:如图,□ABCD中,E、F分别是AD、BC的中点,
求证:BE=DF.
变式练习
A
B
C
D
E
F
已知:如图,E,F是平行四边形ABCD的对角线上的两点,AE=CF.
应用
求证:四边形BEDF是平行四边形.
F
D
A
B
C
E
O
已知:平行四边形ABCD,对角线AC的中点为O,并且E、F分别为OA、OC的中点。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
变式练习
开动脑筋
老师手里有一个平行四边形的玻璃碎片,巧的是刚好从A、C两个顶点断裂。你能用所学的知识帮她补好吗?说说你的想法和理由。
A
B
C
如图,在 ?ABCD中,已知两条对角线相交于点O,E、F、G、H分别是AO、BO、CO、DO的中点,以图中的点为顶点,尽可能多地画出平行四边形。
A
D
C
B
E
F
G
H
O
A
D
C
B
E
F
G
H
O
A
D
C
B
E
F
G
H
O
2、本节课主要运用什么方法来解决一些简单的实际问题?
1、经过本节课的学习,你有哪些收获?
小 结
经过本节课的学习,
你有哪些收获?
请和我们一起分享.
基础题:P49练习第4-6题。
探究题:现有一块等腰直角三角形铁板,要求切割一次焊接成一个含有45°角的平行四边形(不能有余料), 请你设计一种方案,并说明该方案正确的理由.
试金石
A
B
C
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致我亲爱的同学们:
谢谢大家
