人教版八年级下册数学18.1.3平行四边形判定定理的简单应用课件 (共16张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.3平行四边形判定定理的简单应用课件 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:41:09 | ||
图片预览



文档简介
18.1.3平行四边形判定定理的简单应用
1.下列条件能判断四边形ABCD是平行四边形的是( )
①AB∥CD,AD∥BC
②AB=CD,AD= BC
③ OA=OC,OB=OD
④∠DAB=∠DCB,∠ABC=∠ADC
A
B
C
D
O
2.下面给出四边形ABCD中的度数之比,其中能判定四边形ABCD为平行四边形的是( )
A、1:2:3:4 B、2:3:2:3
C、2:2:3:3 D、1:2:2:3
√
√
√
√
B
一、问题诊断
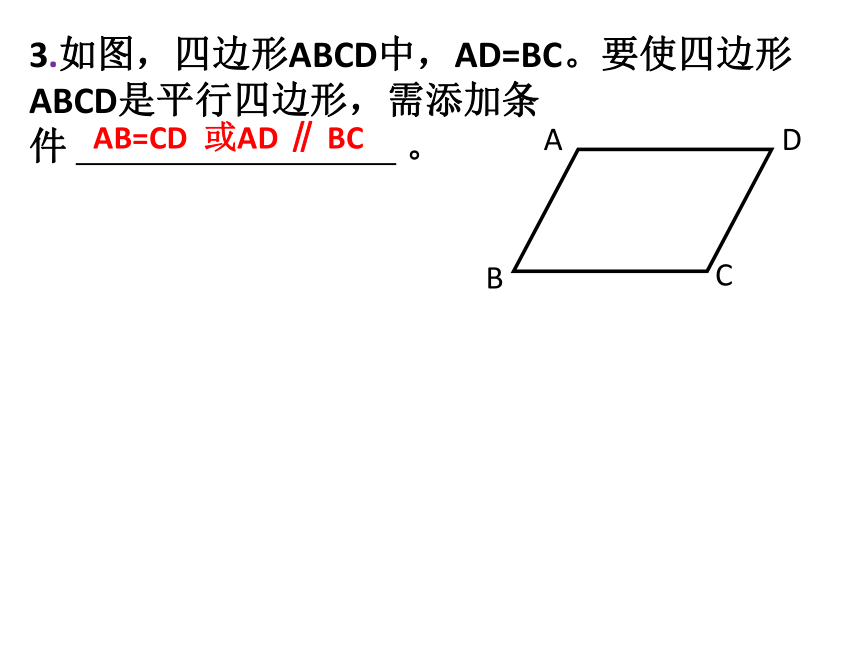
3.如图,四边形ABCD中,AD=BC。要使四边形ABCD是平行四边形,需添加条件 。
A
B
C
D
AB=CD
或AD ∥ BC
二、知识梳理
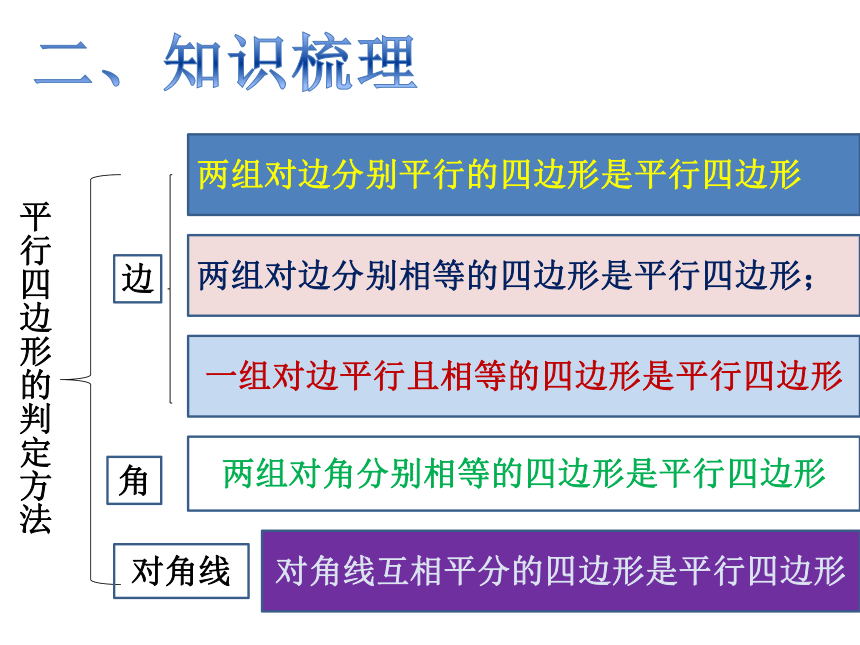
边
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
角
对角线
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
三、典题讲练
A
B
C
D
例1、如图,在四边形ABCD中,AD ∥BC, ∠A= ∠C。
求证:四边形ABCD是平行四边形。
方法一: ∵ AD ∥BC
∴ ∠A+ ∠B=180 °,
∠C+ ∠D=180 °
∵ ∠A= ∠C
∴ ∠B= ∠D
∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形
方法二:连接BD
∵ AD ∥BC
∴ ∠ADB= ∠CBD
∵ ∠A= ∠C,BD=BD
∴ △ADB ≌ △CBD
∴AD=CB
∵ AD ∥BC, AD=CB
∴四边形ABCD是平行四边形
转化:四边形 三角形
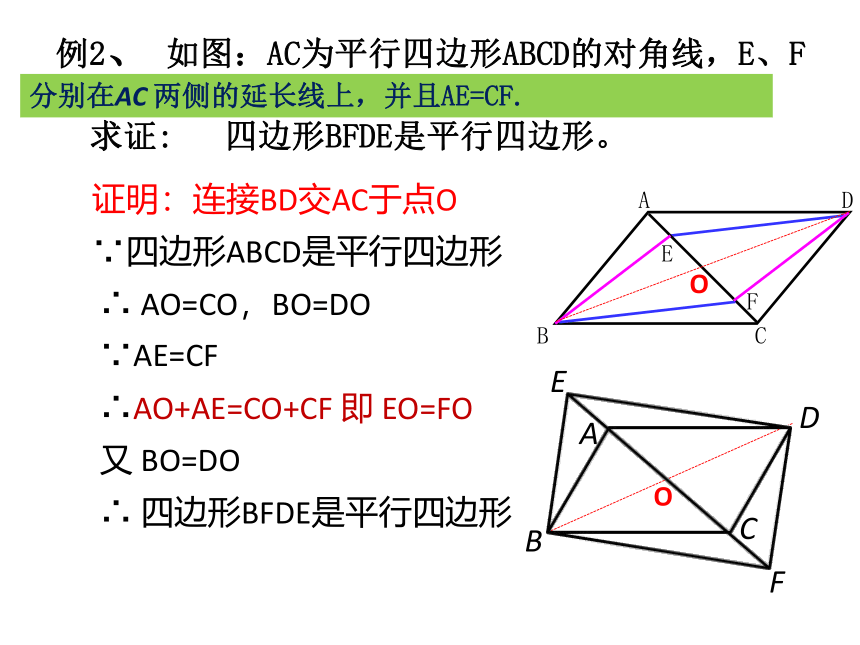
例2、 如图:AC为平行四边形ABCD的对角线,E、F是AC上的两点,并且AE=CF,
求证: 四边形BFDE是平行四边形。
C
B
D
A
F
E
证明:连接BD交AC于点O
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
O
O
证明:连接BD交AC于点O
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO+AE=CO+CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
BE∥DF
A
B
C
D
E
F
分别在AC 两侧的延长线上,并且AE=CF.
四、方法提炼
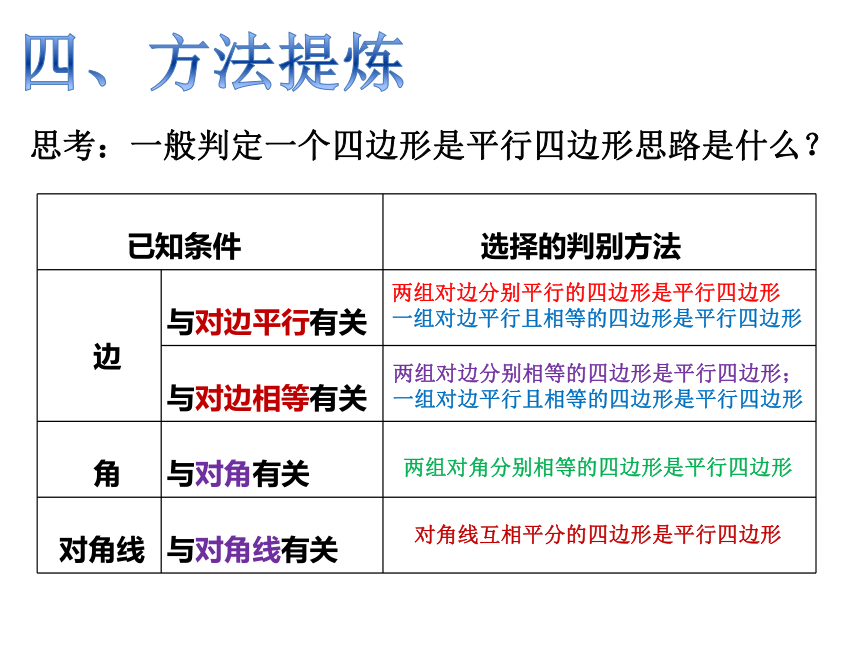
思考:一般判定一个四边形是平行四边形思路是什么?
已知条件
选择的判别方法
边
与对边平行有关
与对边相等有关
角
与对角有关
对角线
与对角线有关
两组对角分别相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
例3 如图,在平行四边形ABCD中,E、F分别是AD,CB的中点.求证:四边形EBFD是平行四边形.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵E,F分别是AD,BC的中点,
∴ED=BF
∵ED=BF,ED∥BF
∴四边形EBFD是平行四边形
求证:BE=DF.
∴ED= AD,BF= BC
五、解决问题
例3 如图,在平行四边形ABCD中,E,F分别是AD,BC的中点
求证:四边形EBFD是平行四边形.
D
F
E
C
B
A
∴ED= AD,BF= BC
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵E,F分别是AD,BC的中点,
∴ED=BF
∵ED=BF,ED∥BF
∴四边形EBFD是平行四边形
AE=CF
∵AE=CF
∴AD-AE=BC-CF
M
N
EB∥FD
∴EB∥FD
四边形MENF为平行四边形
MN与EF互相平分
五、解决问题
例3 如图,在平行四边形ABCD中,AE=BF
求证:MN ∥ BC,MN= BC
D
F
E
C
B
A
M
N
五、解决问题
这节课我们学了哪些知识?你有哪些收获?
六、小结归纳
这节课我们学了哪些知识?你有哪些收获?
方法:简单运用平行四边形的判定方法解决问题。
思想:转化的数学思想(四边形 三角形)
思路:两条线段的数量、位置关系
平行四边形
两条线段的数量、位置关系
判定
性质
六、小结归纳
1.已知,如图,在 平行四边形ABCD中,点E、F
分别是边AB、CD的中点。求证:EF//AD//BC
A
B
C
D
E
F
七、运用提高
2、学校组织数学兴趣小组的同学对“东莞工业区”种植的花圃形状进行检测。提供的工具为:卷尺、量角器。若你所在小组负责测量平行四边形形状的花带是否标准,请问你将如何操作?理由是什么?
3 、 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
A
B
C
D
E
F
再见!
再见
1.下列条件能判断四边形ABCD是平行四边形的是( )
①AB∥CD,AD∥BC
②AB=CD,AD= BC
③ OA=OC,OB=OD
④∠DAB=∠DCB,∠ABC=∠ADC
A
B
C
D
O
2.下面给出四边形ABCD中的度数之比,其中能判定四边形ABCD为平行四边形的是( )
A、1:2:3:4 B、2:3:2:3
C、2:2:3:3 D、1:2:2:3
√
√
√
√
B
一、问题诊断
3.如图,四边形ABCD中,AD=BC。要使四边形ABCD是平行四边形,需添加条件 。
A
B
C
D
AB=CD
或AD ∥ BC
二、知识梳理
边
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
角
对角线
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
三、典题讲练
A
B
C
D
例1、如图,在四边形ABCD中,AD ∥BC, ∠A= ∠C。
求证:四边形ABCD是平行四边形。
方法一: ∵ AD ∥BC
∴ ∠A+ ∠B=180 °,
∠C+ ∠D=180 °
∵ ∠A= ∠C
∴ ∠B= ∠D
∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形
方法二:连接BD
∵ AD ∥BC
∴ ∠ADB= ∠CBD
∵ ∠A= ∠C,BD=BD
∴ △ADB ≌ △CBD
∴AD=CB
∵ AD ∥BC, AD=CB
∴四边形ABCD是平行四边形
转化:四边形 三角形
例2、 如图:AC为平行四边形ABCD的对角线,E、F是AC上的两点,并且AE=CF,
求证: 四边形BFDE是平行四边形。
C
B
D
A
F
E
证明:连接BD交AC于点O
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
O
O
证明:连接BD交AC于点O
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO+AE=CO+CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
BE∥DF
A
B
C
D
E
F
分别在AC 两侧的延长线上,并且AE=CF.
四、方法提炼
思考:一般判定一个四边形是平行四边形思路是什么?
已知条件
选择的判别方法
边
与对边平行有关
与对边相等有关
角
与对角有关
对角线
与对角线有关
两组对角分别相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
例3 如图,在平行四边形ABCD中,E、F分别是AD,CB的中点.求证:四边形EBFD是平行四边形.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵E,F分别是AD,BC的中点,
∴ED=BF
∵ED=BF,ED∥BF
∴四边形EBFD是平行四边形
求证:BE=DF.
∴ED= AD,BF= BC
五、解决问题
例3 如图,在平行四边形ABCD中,E,F分别是AD,BC的中点
求证:四边形EBFD是平行四边形.
D
F
E
C
B
A
∴ED= AD,BF= BC
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵E,F分别是AD,BC的中点,
∴ED=BF
∵ED=BF,ED∥BF
∴四边形EBFD是平行四边形
AE=CF
∵AE=CF
∴AD-AE=BC-CF
M
N
EB∥FD
∴EB∥FD
四边形MENF为平行四边形
MN与EF互相平分
五、解决问题
例3 如图,在平行四边形ABCD中,AE=BF
求证:MN ∥ BC,MN= BC
D
F
E
C
B
A
M
N
五、解决问题
这节课我们学了哪些知识?你有哪些收获?
六、小结归纳
这节课我们学了哪些知识?你有哪些收获?
方法:简单运用平行四边形的判定方法解决问题。
思想:转化的数学思想(四边形 三角形)
思路:两条线段的数量、位置关系
平行四边形
两条线段的数量、位置关系
判定
性质
六、小结归纳
1.已知,如图,在 平行四边形ABCD中,点E、F
分别是边AB、CD的中点。求证:EF//AD//BC
A
B
C
D
E
F
七、运用提高
2、学校组织数学兴趣小组的同学对“东莞工业区”种植的花圃形状进行检测。提供的工具为:卷尺、量角器。若你所在小组负责测量平行四边形形状的花带是否标准,请问你将如何操作?理由是什么?
3 、 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
A
B
C
D
E
F
再见!
再见
