人教版八年级下册数学20.2.2数据的波动程度课件 (共19张PPT)
文档属性
| 名称 | 人教版八年级下册数学20.2.2数据的波动程度课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:29:05 | ||
图片预览






文档简介
双色笔+课本+导学案
还有你的激情!
课堂因你而变得精彩!
积极参与,你将收获多多!
问题1 农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到
各试验田每公顷的产量(单位:t)如下表:
创设情境,提出问题
二、探究新知
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相
差不大.
可估计这个地区种植这两种甜玉米的平均产量相差
不大.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
产量波动较大
产量波动较小
探究新知
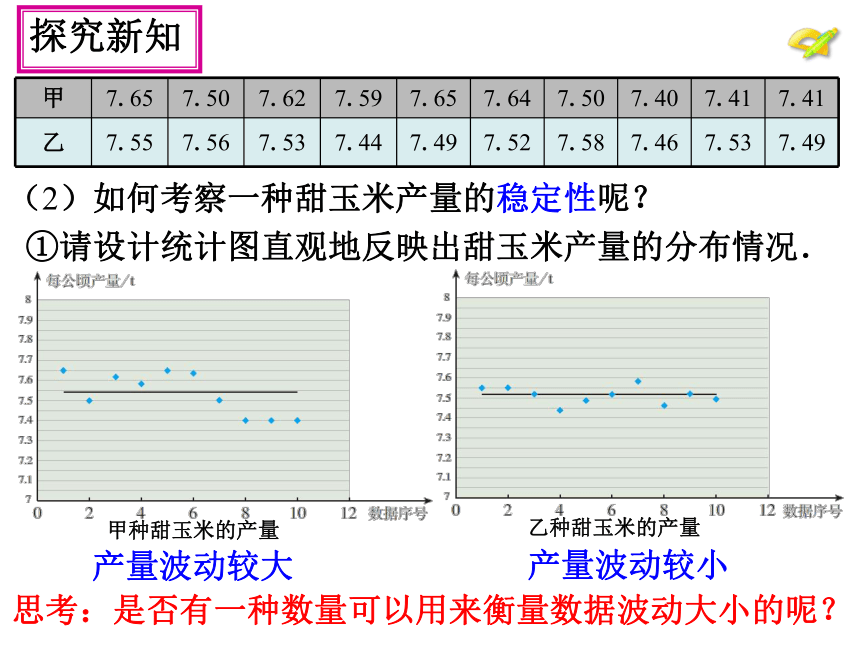
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
甲种甜玉米的产量
乙种甜玉米的产量
思考:是否有一种数量可以用来衡量数据波动大小的呢?
八年级 下册
20.2.2数据的波动程度
【学习目标】
1. 了解方差的定义和计算公式,会用方差比较两组数据的波动大小;
2. 经历探索方差的应用过程,体会数据波动中的方差的求法,积累统计经验;
3. 培养学生的统计意识,形成用数据说话的态度,认识数据处理的实际意义.
【重点】学会用公式求一组数据的方差
【难点】应用方差对数据波动情况的进行
比较、判断.
一、自主学习
1.复习旧知:
(1)一组数据2,4,6的平均数是________;
(2)学校以德智体三项成绩来计算学生的平均成绩,三项成绩的
比例依次为1∶3∶1,小明德智体三项成绩分别为96分,95分,94分,则小明的平均成绩为________分.
2.探究新知:
(1)方差的定义是什么?
?
?
(2)方差的计算公式是什么?
【预习案】
4
95
?
新知学习
统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
例:求数据2,3,4的方差.
?
?
?
思考:方差的意义是什么?
方差的意义:反映一组数据的 大小.方差越大,数据的波动越 ,方差越小,数据的波动越 .当一组数据中的每个数据都相同时,方差= .
波动
越大
越小
0
?
?
解:
B
?
=
?
?
学习建议:全力以赴、
全神贯注、
全员参与。
(1)结合课本和学习目标,认真思考并解决探究案中的内容。
(2)通过习题总结规律及注意的问题。
(3)非展示同学抓紧时间巩固落实各项知识。
展示内容
展示小组
预1例题
1组B1(前黑板)
预习自测2
3组B1(前黑板)
例1
5组B1(后黑板)
例2
7组B1(后黑板)
智慧碰撞 高效展示
点评要求
精彩点评,分享提升
1. 面向同学,声音洪亮,语言精炼,自然大方;
2. 点评时注重对题目思路和方法的分析,点明注意事项,并总结方法和规律;
3.非点评同学要极度专注,积极质疑、追问、补充。
点评内容
点评小组
例1
2组
例2
6组
点评要求
精彩点评,分享提升
1. 面向同学,声音洪亮,语言精炼,自然大方;
2. 点评时注重对题目思路和方法的分析,点明注意事项,并总结方法和规律;
3.其他同学要极度专注,积极质疑、追问、补充。
【探究案】
探究点:方差在生活实际中的作用
例1. 下表是甲、乙两名射击运动员在相同条件下各射靶5次命中的环数:
甲
5
8
8
9
10
乙
9
6
10
5
10
(1)分别计算两人的平均成绩;
(2)求出每组数据的方差;
(3)谁的射击成绩比较稳定,派谁参赛比较合适?
?
?
?
?
?
?
例2.某实验中学八年级甲、乙两班分别选5名同学参加演讲比赛,其预赛成绩如下图所示:
(1)根据上图填写下表:
班级
平均数
中位数
众数
方差
甲班
?
8.5
?
?
乙班
?
?
10
1.6
(2)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
?
(3)你认为哪班的成绩较好?并说明你的理由;
?
思考:1.如何计算方差?2.方差在生活实际中有什么作用?
8.5
8.5
8
8.5
0.7
解:小明是5号选手,因为乙班成绩的中位数是8,5号选手的成绩是8.
解:我认为甲班成绩较好,因为两个班的成绩的平均数一样,
但甲班成绩更稳定.
【课堂小结】
1. 这节课你学到了什么?
2.你认为应该注意什么问题?
【当堂检测】
(基础训练)
1.样本方差的作用是( )
A.估计总体的平均水平 B.表示样本的平均水平
C.表示总体的波动大小 D.表示样本的波动大小,从而估计总体的波动大小
2.体育课上,八年级(6)班两个组各10人参加立定跳远,要判断哪一组比较整齐,通常需要知道这两个组立定跳远成绩的( )
A. 平均数 B. 众数 C. 方差 D. 频率分布
3.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,
方差分别为
则四人中成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
4.数据“1,2,1,3,1” 的平均数是 ,中位数是 ,众数是 ,方差是 .
?
D
C
B
1.6
1
1
0.64
(巩固提升)
5.如果一组数据1,2,3,4,5的方差是2,那么一组新数据101,102,103,104,105的方差是 .
2
(拓展延伸)
6.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活90%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示:
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;(2)根据样本数据请计算说明哪个山上的杨梅产量较稳定.
还有你的激情!
课堂因你而变得精彩!
积极参与,你将收获多多!
问题1 农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到
各试验田每公顷的产量(单位:t)如下表:
创设情境,提出问题
二、探究新知
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相
差不大.
可估计这个地区种植这两种甜玉米的平均产量相差
不大.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
产量波动较大
产量波动较小
探究新知
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
甲种甜玉米的产量
乙种甜玉米的产量
思考:是否有一种数量可以用来衡量数据波动大小的呢?
八年级 下册
20.2.2数据的波动程度
【学习目标】
1. 了解方差的定义和计算公式,会用方差比较两组数据的波动大小;
2. 经历探索方差的应用过程,体会数据波动中的方差的求法,积累统计经验;
3. 培养学生的统计意识,形成用数据说话的态度,认识数据处理的实际意义.
【重点】学会用公式求一组数据的方差
【难点】应用方差对数据波动情况的进行
比较、判断.
一、自主学习
1.复习旧知:
(1)一组数据2,4,6的平均数是________;
(2)学校以德智体三项成绩来计算学生的平均成绩,三项成绩的
比例依次为1∶3∶1,小明德智体三项成绩分别为96分,95分,94分,则小明的平均成绩为________分.
2.探究新知:
(1)方差的定义是什么?
?
?
(2)方差的计算公式是什么?
【预习案】
4
95
?
新知学习
统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
例:求数据2,3,4的方差.
?
?
?
思考:方差的意义是什么?
方差的意义:反映一组数据的 大小.方差越大,数据的波动越 ,方差越小,数据的波动越 .当一组数据中的每个数据都相同时,方差= .
波动
越大
越小
0
?
?
解:
B
?
=
?
?
学习建议:全力以赴、
全神贯注、
全员参与。
(1)结合课本和学习目标,认真思考并解决探究案中的内容。
(2)通过习题总结规律及注意的问题。
(3)非展示同学抓紧时间巩固落实各项知识。
展示内容
展示小组
预1例题
1组B1(前黑板)
预习自测2
3组B1(前黑板)
例1
5组B1(后黑板)
例2
7组B1(后黑板)
智慧碰撞 高效展示
点评要求
精彩点评,分享提升
1. 面向同学,声音洪亮,语言精炼,自然大方;
2. 点评时注重对题目思路和方法的分析,点明注意事项,并总结方法和规律;
3.非点评同学要极度专注,积极质疑、追问、补充。
点评内容
点评小组
例1
2组
例2
6组
点评要求
精彩点评,分享提升
1. 面向同学,声音洪亮,语言精炼,自然大方;
2. 点评时注重对题目思路和方法的分析,点明注意事项,并总结方法和规律;
3.其他同学要极度专注,积极质疑、追问、补充。
【探究案】
探究点:方差在生活实际中的作用
例1. 下表是甲、乙两名射击运动员在相同条件下各射靶5次命中的环数:
甲
5
8
8
9
10
乙
9
6
10
5
10
(1)分别计算两人的平均成绩;
(2)求出每组数据的方差;
(3)谁的射击成绩比较稳定,派谁参赛比较合适?
?
?
?
?
?
?
例2.某实验中学八年级甲、乙两班分别选5名同学参加演讲比赛,其预赛成绩如下图所示:
(1)根据上图填写下表:
班级
平均数
中位数
众数
方差
甲班
?
8.5
?
?
乙班
?
?
10
1.6
(2)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
?
(3)你认为哪班的成绩较好?并说明你的理由;
?
思考:1.如何计算方差?2.方差在生活实际中有什么作用?
8.5
8.5
8
8.5
0.7
解:小明是5号选手,因为乙班成绩的中位数是8,5号选手的成绩是8.
解:我认为甲班成绩较好,因为两个班的成绩的平均数一样,
但甲班成绩更稳定.
【课堂小结】
1. 这节课你学到了什么?
2.你认为应该注意什么问题?
【当堂检测】
(基础训练)
1.样本方差的作用是( )
A.估计总体的平均水平 B.表示样本的平均水平
C.表示总体的波动大小 D.表示样本的波动大小,从而估计总体的波动大小
2.体育课上,八年级(6)班两个组各10人参加立定跳远,要判断哪一组比较整齐,通常需要知道这两个组立定跳远成绩的( )
A. 平均数 B. 众数 C. 方差 D. 频率分布
3.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,
方差分别为
则四人中成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
4.数据“1,2,1,3,1” 的平均数是 ,中位数是 ,众数是 ,方差是 .
?
D
C
B
1.6
1
1
0.64
(巩固提升)
5.如果一组数据1,2,3,4,5的方差是2,那么一组新数据101,102,103,104,105的方差是 .
2
(拓展延伸)
6.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活90%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示:
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;(2)根据样本数据请计算说明哪个山上的杨梅产量较稳定.
