人教版八年级下册数学19.2一次函数复习课件(共79张ppt))
文档属性
| 名称 | 人教版八年级下册数学19.2一次函数复习课件(共79张ppt)) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览











文档简介
一次函数
努力进取,永不言败!
目 标:
1、理解并熟记什么是一次函数。
2、理解正比例函数与一次函数的区别和联系。
3、灵活掌握一次函数的性质。
4、会画并灵活应用一次函数图像。
思考:下列问题中的对应关系可用怎样的函数表示?
(1)有人发现,在20~50 ℃时蟋蟀每分鸣叫的次数c与温度t(单位: ℃)有关,即c的值约是t的7倍与35的差;
解:C=7t-35
A组
(2)一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h,再减去常数105,所得差是G的值;
(3)某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拔打电话x分的计时费(按0.1元/分收取);
(4)把一个长10cm、宽5cm的长方形的长减少x cm,宽不变,长方形的面积y(单位:平方厘米)随x的值而变化
解:G=h-105
解:y=0.1x+22
解:y=-5x+50 (0≤x≤10)
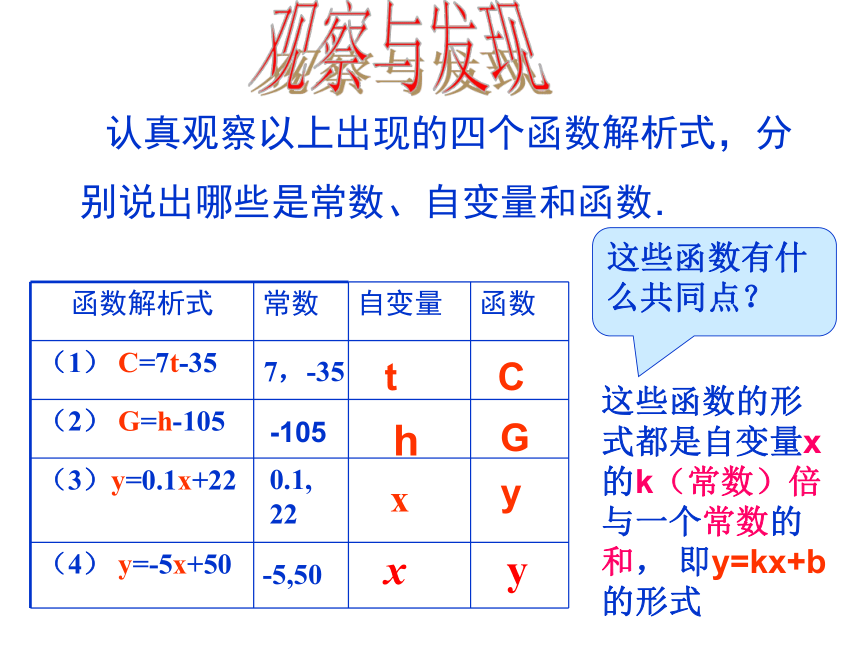
认真观察以上出现的四个函数解析式,分
别说出哪些是常数、自变量和函数.
函数解析式
常数
自变量
函数
(1) C=7t-35
(2) G=h-105
(3)y=0.1x+22
(4) y=-5x+50
这些函数有什么共同点?
这些函数的形式都是自变量x的k(常数)倍与一个常数的和, 即y=kx+b的形式
7,-35
t
C
-105
h
G
0.1, 22
x
y
-5,50
x
y
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数。
正比例函数和一次函数有什么区别和联系?
联系:正比例函数是一种特殊的一次函数,
一次函数不一定是正比例函数。
区别:一次函数有常数项,
正比例函数常数项为零。
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
练习:下列哪些函数是一次函数,哪些又是正比例函数.k和b的值是?
是一次函数,k=-3,b=-4
不是
是正比例函数,也是一次函数
不是
不是
2.已知下列函数:y=2x+1;
;s=60t;y=100-25x,其中表示
一次函数的有( )
(A )1个
( B)2个
( C)3个
( D)4个
D
3.下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数
(D)不是正比例函数就不是一次函数
D
例: 若函数y=(m-1)x|m|+m是关于x的一次函数,
试求m的值.
解,∵函数为一次函数,
m-1≠0
∴
|m|=1
m=±1,
∴
m ≠1
则m=-1
所以当m=-1函数y=(m-1)x|m|+m是关于x的一次函数,
4.要使y=(m-2)xn-1+n是关于x的
一次函数,n,m应满足 , .
n=2
m≠2
5.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为正比例函数
(2)此函数为一次函数
解:(1)由题意, 得2m-3=0,m= ,所以当
m= 时,函数为正比例函数y= x
(2)由题意得2-m≠0, m≠2,所以m≠2时,此函数为一次函数
.6.汽车油箱中原有油50升,如果行驶中每
千米用油5升,求油箱的油量y(单位:升)随
行使路程x(单位:千米)变化的函数关系式,
并写出自变量x的取值范围.y是x的一次
函数吗?
解:由题意得,函数关系式为y=50-5x.
自变量x的取值范围是0≤x≤10
y是x的一次函数.
7.一个小球由静止开始在一个斜坡向下滚动,其速度每秒增加2米。
(1)求小球速度v随时间t变化的函数关系式,它是一次函数吗?
(2)求第2.5秒时小球的速度.
解: (1)由已知得,函数关系式为v=2t
是一次函数,
(2)当t=2.5秒时,v=5米/秒
8.思考 小明根据某个一次函数关系式填写了下表:
x
-2
-1
0
1
y
3
1
0
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
作出一次函数y=2x和Y=2X+1的图象
1、列表:分别选取若干对自变量与函数的对应值,列成下表.
2、描点:分别以表中的X作为横坐标,Y作为纵坐标,得到两组点,写出这些点(用坐标表示).再画一个平面直角坐标系,并在坐标系中画出这些点.
X
….
-2
-1
0
1
2
….
Y=2X
….
….
Y=2X+1
….
….
-4
-3
-2
-1
0
1
2
3
4
5
B组
Y
X
O
Y=2X
Y=2X+1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
1
2
3
4
5
6
7
8
-7
-8
这两个函数的图象形状都是 ,
并且倾斜程度 .函数y=2x的图象经过原点,函数y=2x+1的图象与y轴交于点 ,即它可以看作直线y=2x向 平移 个单位长度而得到
直线
相同
(0,1)
上
1
x
y
2
0
.
.
.
.
.
.
.
请比较下列函数y=x, y=x+2,y=x-2的图象有什么异同点?
.
.
.
.
y=x
.
.
.
.
y=x+2
y=x-2
这几个函数的图象形状都是 ,并且倾斜程度__ _函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
直线y=kx+b可以看作直线y=kx向上(或向下)平移 |b| 个单位长度得到的
当b<0时,向下平移
当b>0时,向上平移
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
特性:
x
y
o
y = k1x+b1
▲k1=k2=k3 b1≠b2≠b3三线平行
y = k2x+b2
y = k3x+b3
y=x
y=x+2
y=x-2
y
3
0
x
2
.
一次函数y=kx+b的图象
是经过(0,b)点且平行于
直线y=kx的一条直线,
我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单
位长度得到. (当b>0时,向上平移;当b<0时,
向下平移)
图象与y轴交于(0,b),
b就是与y轴交点的纵坐标,
(0,b)
归纳总结
结论:一次函数y=kx+b的图象是一条
_____,我们称它为直线y=kx+b,它可
以看作由________平移___个单位长度
而得到
直线
直线y=kx
|b|
(当b>0时,向上平移;当 b<0,向下平移)
猜想:考虑一次函数y=kx+b的图像是什么形状?
它与直线y=kx有什么关系?
一次函数 y = k x + b(k≠0)
(1) 当 x = 0 时, y =0 · k + b = b,
所以一次函数 y = k x + b 经过 ( 0 , b ) 点.
(2) 当 y = 0 时, k x + b = 0, x = -
—
b
k
—
b
k
所以一次函数 y = k x + b 经过 (- , 0) 点.
一次函数 y = k x + b (k≠0)是 经过 ( 0 , b )
和(- , 0)的一条直线.
—
b
k
你会画出函数
y=2x-1与 y=-0.5x+1 的图象吗?
y
x
o
1
1
·
·
·
·
y=2x-1
y=-0.5x+1
x
0
1
y=2x -1
y=-0.5x+1
-1
1
1
0.5
方法1、平移法
方法2、描点法
(1)先画y=2x,再向下平移1个单位
(2)先画 ,再向 平移 个 单位
I I I I I
I I I I I
1
-1
.
.
.
y=2x
y=2x-1
1
x
y
-1
y=-0.5x
上
1
2
(1)直线y=3x-2可由直线y=3x向 平移 单位得到。
(2)直线y=x+2可由直线y=x-1向 平移 单位得到。
下
2
上
3
?
4、 直线 y = -3x – 1
过点(___ , 0 )和( 0,__ ).
练习一
3、 直线y=4x+2
过点( 0 ,__)和( __, 0 ).
2
- —
1
2
- —
1
3
-1
6、一次函数y=2x-1的图象是一条经过点(0,____)
和(____ ,0)且平行于直线__________的直线。
-1
y=2x
7、一次函数y=kx+b的图象是一条经过点(0,__)
和(____,0)且平行于直线_______的直线。
b
y=kx
5、把直线 向上平移3个单位长度所
得到的解析式为
y
x
o
1
1
·
·
y=2x-1
y=-2x+l
探究:画出函数y=x+1,y=2x-1及y=-x-1 y=-2x+l的图象
y=x+1
y=-x-1
并思考:
一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?(
经过哪几个象限)
-1
-1
C组
y
x
o
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
y=2x
y=2x+3
y=2x-4
⑴当k>0, 图象经过一、 三象限;
一次函数y=k x + b(k≠0)的图象
b>0
二、
⑵当 k>0, b<0
图象经过一、三、
四象限;
当k>0时,函数的图象从左到右上升,y随x的增大而增大
x
y
o
y=k x(k<0)
⑶当 k < 0, b > 0
图象经过一、二、四象限;
⑷当 k < 0, b < 0
图象经过二、 三、四象限;
一次函数y=k x + b(k≠0)的图象
y=kx+b
y=kx+b
当k<0时,函数的图象从左到右下降,y随x的增大而减小
y=k x+b
图像的位置
b>0
b<0
k>0
k<0
一次函数y= k x+b(k≠0)的图象
图象经过一、二、三象限
图象经过一、三、四象限
图象经过一、二、四象限
图象经过
二、三、四象限
y
o
x
y
o
x
y
o
x
y
o
x
根据函数图象确定k,b的取值范围
y
x
o
K>o, b=o
K>0, by
x
o
K>o, b>0
y
x
o
K<0, b=0
y
x
o
K<0, b<0
y
x
o
K<0, b>0
y
x
0
看图象,确定一次函数y=kx+b(k≠0)
中k,b的符号。
o
x
y
o
x
y
o
x
y
k<0
b<0
k>0
b>0
k<0
b=0
已知一次函数y=kx+b(k≠0)中
①k>0,b<0 ②k<0,b>0,试作草图。
o
y
x
o
y
x
例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数y的值怎样变化?
o
x
1
2
3
4
-1
-2
-3
-4
1
1
2
3
4
-1
-2
y
解:
y= -2x+1
y =2x+1
x
0
-1/2
y =2x+1
1
0
x
0
1/2
y=-2x+1
1
0
(0,1)
(-1/2,0)
(1/2,0)
一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大;
y
x
一次函数y=kx+b (k?0)的性质:
当k<0时,y随x的增大而减小.
y
x
一次函数通常选取(0,b),
(-b/k,0)两点连线
一次函数 y = kx + b ( k ≠ 0 ) 有以下性质:
(1)当 k > 0 时,y 随 x 的增大而 。
(2)当 k < 0 时,y 随 x 的增大而 。
增大
减小
一次函数图象与性质
一次函数y=kx+b(b≠0)
图象
k,b的符号
经过象限
增减性
x
y
o
b
x
y
o
b
x
y
o
b
x
y
o
b
y随x的增
大而增大
y随x的增
大而增大
y随x的增
大而减少
y随x的增
大而减少
一、二、三
一、三、四
一、二、四
二、三、四
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
例、已知一次函数y=(m-1)x+2m+1。
(4)若图象经过一、二、四象限,
求m的取值范围。
解:由题意可知 k<0, b>0
m-1<0
2m+ 1 >0
m<1
m> -1/2
所以 -1/2 < m<1.
知识应用
练习:已知函数y=(m-2)x+n的
图象经过一、二、三象限.
求 : m、n的取值范围.
直线y=kx+b经过一、二、四象限,那么直线y=bx+k经过哪些象限?
思维拓展
3、直线y=-x-3经过___________象限
二、三、四
4、已知函数y=kx+2,且y随x的增大而增大,
则它的图象不经过第_____象限
四
考考你
5、一次函数y=kx+b,kb>0,且y随x的增大
而减小,则它的图象可能是 ( )
C
考考你
6、已知一次函数y=(a-1)x+b的图象如图所示,
那么a、b的取值范围是 ( )
A.a>1,b>0
B.a<1,b>0
C.a>1,b<0
D.a<1,b<0
A
考考你
y
x
0
(D)
y
x
0
(A )
y
x
0
( C )
y
x
0
(B)
逆向思维 小试牛刀
7、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
B
8、已知一次函数y = mx-(m-2),
若它的图象经过原点,则 m= ;
若点(0 ,3) 在它的图象上,则m = ;若它的图象经过一、二、四象限,则m .
2
-1
<0
9.对于一次函数y = mx-(m-2),若y 随x 的增大而增小,则其图象不
过 象限。
10.若直线 y = kx -3 过(2, 5),
则k = ;
若此直线平行于直线y = - 3x - 5,
则k= .
三
4
-3
D组:达标检测
1在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限
2已知一次函数y=x-2的大致图像为 ( )
A B C D
D
C
3.已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
(4)对于函数y=5x+6,k=__,b=__,y随x的增大而 ,反之y随x的减小而____.
增大
减小
5
6
(5)直线y=2x - 6与y轴的交点为 (_____),与x轴交于(_____)
0,-6
3, 0
6、 将函数y= - 2x的图象沿y轴向上平移
5个单位,得到的直线的解析式为
__________,图象经过第________
象限。
7、 将函数y= -0.5x的图象沿y轴向下平移
3个单位,得到的直线的解析式为
_________ ,图象经过第________
象限。
y= - 2x+5
一、二、四
y= -0.5x-3
二、三、四
8、函数y=(1-k)x中y随x的增大而减小,则k的范围是 .
k>1
9、直线y=-3x-6与x轴的交点坐标是 ,与y轴的交点坐标为 .
(-2,0)
(0,-6)
10、直线y=3x-1经过 象限;
一、三、四
11、若一次函数y=kx+b随x的增大y增大,且
kb>0,那么该直线不经过第 ————象限
四
12、直线y=kx+b的图象如图所示,确定k、b符号:
o
y
x
o
y
x
K<0,b>0
k>0,b<0
13、下图中哪一个是 y = x - 1的大致图像?
A
B
C
D
14、一次函数y=kx-k的图象可能是( )
A
B
C
D
C
15、已知一次函数y=(m-1)x+2m+1。
若图象平行于直线y=2x,求m的值
解:由题意可得 m – 1 = 2
所以 m = 3,
即y =(m-1)x+2m+1 = 2x + 7.
www.czsx.com.cn
16、已知一次函数y=(m-1)x+2m+1。
若图象交y轴于正半轴,求m的取值范围
解:
若图象交 y 轴于正半轴,
b>0,
2m+1>0
m-1≠0
m>-1/2
m≠1
所以 m>-1/2 且 m≠1。
1.设一次函数的一般形式y=kx+b(k≠0) ;
2.根据已知条件列出关于k , b 的二元一次方程组
3.解这个方程组,解出k, b ;
4 .将已经求出的 k, b的值代入所设解析式.
写出这个解析式
解题的步骤:
待定系数法:
像刚才这样先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,解出未知系数,从而得到所求结果的方法,叫做待定系数法.
1. 已知一次函数的图象如图所示,求该函数的解析式。
0 1 2 3 4 5 x
y
5
4
3
2
1
解:设这个一次函数的解析式为y=kx+b。
∴ b=3
3k+b=0
解方程组得 k=1
b=3
∴这个一次函数的解析式
为y= x+3。
(k≠0)从图中可以看出 图象过点(0,3)与(3,0)。
0 1 2 3 4 5 x
y
5
4
3
2
1
函数解析式y=kx+b(k≠0)
选取
解出
满足条件的两点(x1,y1)与(x2,y2)
一次函数的图象
直线
画出
选取
从数到形
从形到数
数学的思想方法:数形结合
x
0
y
-9
-4
B
A
3
5
由于两点确定了一条直线,即这个图象是一次函数y = kx+b
y = kx+b
A(3,5),
B(-4,-9)
解:因为图象是一次函数,所以设函数的解析式
为y = kx+b
且图象过点A(3,5)和点B(-4,-9),所以
由①-②得
∴这个函数的解析式为y = 2x-1
①
②
y
x
5
3
-4
-9
0
A
B
①
②
①
②
①
②
A
B
C
2.如图,一次函数的图象过点A且与正比例函数y=-x的图象交于点B。那么该一次函数的表达式为
-1 0 x
y=-x
2
A
B
y
y=x+2
若直线l与直线y= x-1关于x轴对称,则直线l的解析式为_____________。
1
2
y=- x+1
1
2
0 1 2 x
y
1
-1
A(2,0)
B(0,-1)
B1(0,1)
y= x-1
1
2
y=- x+1
1
2
总结:
若l直线与直线y = kx+b关于
(1)x轴对称,则直线l的解析式为 y = -kx-b,
即将 y 换成 –y 。
(2)y轴对称,则直线l的解析式为 y = -kx+b,
即将 x 换成 -x。
(3) 原点对称,则直线l的解析式为 y=kx-b,
即将y换成-y,x换成-x。
若直线l与直线y= x-1关于y轴对称,
则直线l的解析式为_____________。
想一想
若直线l与直线y= x-1关于原点对称,则直线l的解析式为_____________。
1
2
1
2
y=- x-1
1
2
y= x+1
1
2
例2 已知直线y=kx+b与直线y=2x平行且过点(-1,4),则k=___,b=___。
3.已知一次函数y=kx+b的图象与y=-3x+4的图象平行且与y轴相交于点(0,3)。则这个函数的解析式为__________________。
y=-3x+3
2
6
4.直线y=kx+b经过点A(-3,0)且与y轴交于点B,如果△AOB的(0为坐标原点)面积为4.5,则这条直线的解析式为( )。
A.y=x+3
B.y=-x-3
C.y=x+3或y=-x-3
D.y=x+3或y=x-3
·
(-3,0)
x
y
o
c
5、已知函数y=kx+b的图象经过点A(4,0),且与两坐标轴所围成的三角形的面积为6,则此函数的解析式为____________.
(4,0)
(0,3)
(0,-3)
A
B
B’
一次函数的图象与坐标轴所围成的面积问题,我们往往要进行分类讨论!
某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
①
②
解得
1.已知直线y=(2m-1)x+m与直线y=x-2平行,且与直线y= x+2n-3 交 y 轴于同一点,则m= ____, n=___.
2.如果要通过平移直线 得到 的图象,那么直线 必须向___平移___个 单位.
3.如果直线y =kx+b平行于直线y=2x+4,且与两坐标轴围成的三角形的面积为8,求直线y =kx+b 的解析式.
1、用待定系数法求一次函数的解析式。
2、数与形的关系----数形结合的思想。
课堂小结
3、对有些题目要分情况进行讨论——分类讨论的思想。
1、怎样的函数是一次函数?
一般地,形如y=kx+b(k,b是常数,k≠0)
的函数,叫做一次函数。
2、会区分一次函数与正比例函数
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数。
3、怎么画一次函数图像?
一次函数y=kx+b的图象是一条_____,我们称它为直线y=kx+b,它可以看作由________平移___个单位长度而得到
直线
直线y=kx
|b|
(当b>0时,向上平移;当b<0,向下平移)
平移法、描点法
4、一次函数y=kx+b的性质
5.用待定系数法求解析式
努力进取,永不言败!
目 标:
1、理解并熟记什么是一次函数。
2、理解正比例函数与一次函数的区别和联系。
3、灵活掌握一次函数的性质。
4、会画并灵活应用一次函数图像。
思考:下列问题中的对应关系可用怎样的函数表示?
(1)有人发现,在20~50 ℃时蟋蟀每分鸣叫的次数c与温度t(单位: ℃)有关,即c的值约是t的7倍与35的差;
解:C=7t-35
A组
(2)一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h,再减去常数105,所得差是G的值;
(3)某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拔打电话x分的计时费(按0.1元/分收取);
(4)把一个长10cm、宽5cm的长方形的长减少x cm,宽不变,长方形的面积y(单位:平方厘米)随x的值而变化
解:G=h-105
解:y=0.1x+22
解:y=-5x+50 (0≤x≤10)
认真观察以上出现的四个函数解析式,分
别说出哪些是常数、自变量和函数.
函数解析式
常数
自变量
函数
(1) C=7t-35
(2) G=h-105
(3)y=0.1x+22
(4) y=-5x+50
这些函数有什么共同点?
这些函数的形式都是自变量x的k(常数)倍与一个常数的和, 即y=kx+b的形式
7,-35
t
C
-105
h
G
0.1, 22
x
y
-5,50
x
y
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数。
正比例函数和一次函数有什么区别和联系?
联系:正比例函数是一种特殊的一次函数,
一次函数不一定是正比例函数。
区别:一次函数有常数项,
正比例函数常数项为零。
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
练习:下列哪些函数是一次函数,哪些又是正比例函数.k和b的值是?
是一次函数,k=-3,b=-4
不是
是正比例函数,也是一次函数
不是
不是
2.已知下列函数:y=2x+1;
;s=60t;y=100-25x,其中表示
一次函数的有( )
(A )1个
( B)2个
( C)3个
( D)4个
D
3.下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数
(D)不是正比例函数就不是一次函数
D
例: 若函数y=(m-1)x|m|+m是关于x的一次函数,
试求m的值.
解,∵函数为一次函数,
m-1≠0
∴
|m|=1
m=±1,
∴
m ≠1
则m=-1
所以当m=-1函数y=(m-1)x|m|+m是关于x的一次函数,
4.要使y=(m-2)xn-1+n是关于x的
一次函数,n,m应满足 , .
n=2
m≠2
5.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为正比例函数
(2)此函数为一次函数
解:(1)由题意, 得2m-3=0,m= ,所以当
m= 时,函数为正比例函数y= x
(2)由题意得2-m≠0, m≠2,所以m≠2时,此函数为一次函数
.6.汽车油箱中原有油50升,如果行驶中每
千米用油5升,求油箱的油量y(单位:升)随
行使路程x(单位:千米)变化的函数关系式,
并写出自变量x的取值范围.y是x的一次
函数吗?
解:由题意得,函数关系式为y=50-5x.
自变量x的取值范围是0≤x≤10
y是x的一次函数.
7.一个小球由静止开始在一个斜坡向下滚动,其速度每秒增加2米。
(1)求小球速度v随时间t变化的函数关系式,它是一次函数吗?
(2)求第2.5秒时小球的速度.
解: (1)由已知得,函数关系式为v=2t
是一次函数,
(2)当t=2.5秒时,v=5米/秒
8.思考 小明根据某个一次函数关系式填写了下表:
x
-2
-1
0
1
y
3
1
0
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
作出一次函数y=2x和Y=2X+1的图象
1、列表:分别选取若干对自变量与函数的对应值,列成下表.
2、描点:分别以表中的X作为横坐标,Y作为纵坐标,得到两组点,写出这些点(用坐标表示).再画一个平面直角坐标系,并在坐标系中画出这些点.
X
….
-2
-1
0
1
2
….
Y=2X
….
….
Y=2X+1
….
….
-4
-3
-2
-1
0
1
2
3
4
5
B组
Y
X
O
Y=2X
Y=2X+1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
1
2
3
4
5
6
7
8
-7
-8
这两个函数的图象形状都是 ,
并且倾斜程度 .函数y=2x的图象经过原点,函数y=2x+1的图象与y轴交于点 ,即它可以看作直线y=2x向 平移 个单位长度而得到
直线
相同
(0,1)
上
1
x
y
2
0
.
.
.
.
.
.
.
请比较下列函数y=x, y=x+2,y=x-2的图象有什么异同点?
.
.
.
.
y=x
.
.
.
.
y=x+2
y=x-2
这几个函数的图象形状都是 ,并且倾斜程度__ _函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
直线y=kx+b可以看作直线y=kx向上(或向下)平移 |b| 个单位长度得到的
当b<0时,向下平移
当b>0时,向上平移
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
特性:
x
y
o
y = k1x+b1
▲k1=k2=k3 b1≠b2≠b3三线平行
y = k2x+b2
y = k3x+b3
y=x
y=x+2
y=x-2
y
3
0
x
2
.
一次函数y=kx+b的图象
是经过(0,b)点且平行于
直线y=kx的一条直线,
我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单
位长度得到. (当b>0时,向上平移;当b<0时,
向下平移)
图象与y轴交于(0,b),
b就是与y轴交点的纵坐标,
(0,b)
归纳总结
结论:一次函数y=kx+b的图象是一条
_____,我们称它为直线y=kx+b,它可
以看作由________平移___个单位长度
而得到
直线
直线y=kx
|b|
(当b>0时,向上平移;当 b<0,向下平移)
猜想:考虑一次函数y=kx+b的图像是什么形状?
它与直线y=kx有什么关系?
一次函数 y = k x + b(k≠0)
(1) 当 x = 0 时, y =0 · k + b = b,
所以一次函数 y = k x + b 经过 ( 0 , b ) 点.
(2) 当 y = 0 时, k x + b = 0, x = -
—
b
k
—
b
k
所以一次函数 y = k x + b 经过 (- , 0) 点.
一次函数 y = k x + b (k≠0)是 经过 ( 0 , b )
和(- , 0)的一条直线.
—
b
k
你会画出函数
y=2x-1与 y=-0.5x+1 的图象吗?
y
x
o
1
1
·
·
·
·
y=2x-1
y=-0.5x+1
x
0
1
y=2x -1
y=-0.5x+1
-1
1
1
0.5
方法1、平移法
方法2、描点法
(1)先画y=2x,再向下平移1个单位
(2)先画 ,再向 平移 个 单位
I I I I I
I I I I I
1
-1
.
.
.
y=2x
y=2x-1
1
x
y
-1
y=-0.5x
上
1
2
(1)直线y=3x-2可由直线y=3x向 平移 单位得到。
(2)直线y=x+2可由直线y=x-1向 平移 单位得到。
下
2
上
3
?
4、 直线 y = -3x – 1
过点(___ , 0 )和( 0,__ ).
练习一
3、 直线y=4x+2
过点( 0 ,__)和( __, 0 ).
2
- —
1
2
- —
1
3
-1
6、一次函数y=2x-1的图象是一条经过点(0,____)
和(____ ,0)且平行于直线__________的直线。
-1
y=2x
7、一次函数y=kx+b的图象是一条经过点(0,__)
和(____,0)且平行于直线_______的直线。
b
y=kx
5、把直线 向上平移3个单位长度所
得到的解析式为
y
x
o
1
1
·
·
y=2x-1
y=-2x+l
探究:画出函数y=x+1,y=2x-1及y=-x-1 y=-2x+l的图象
y=x+1
y=-x-1
并思考:
一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?(
经过哪几个象限)
-1
-1
C组
y
x
o
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
y=2x
y=2x+3
y=2x-4
⑴当k>0, 图象经过一、 三象限;
一次函数y=k x + b(k≠0)的图象
b>0
二、
⑵当 k>0, b<0
图象经过一、三、
四象限;
当k>0时,函数的图象从左到右上升,y随x的增大而增大
x
y
o
y=k x(k<0)
⑶当 k < 0, b > 0
图象经过一、二、四象限;
⑷当 k < 0, b < 0
图象经过二、 三、四象限;
一次函数y=k x + b(k≠0)的图象
y=kx+b
y=kx+b
当k<0时,函数的图象从左到右下降,y随x的增大而减小
y=k x+b
图像的位置
b>0
b<0
k>0
k<0
一次函数y= k x+b(k≠0)的图象
图象经过一、二、三象限
图象经过一、三、四象限
图象经过一、二、四象限
图象经过
二、三、四象限
y
o
x
y
o
x
y
o
x
y
o
x
根据函数图象确定k,b的取值范围
y
x
o
K>o, b=o
K>0, b
x
o
K>o, b>0
y
x
o
K<0, b=0
y
x
o
K<0, b<0
y
x
o
K<0, b>0
y
x
0
看图象,确定一次函数y=kx+b(k≠0)
中k,b的符号。
o
x
y
o
x
y
o
x
y
k<0
b<0
k>0
b>0
k<0
b=0
已知一次函数y=kx+b(k≠0)中
①k>0,b<0 ②k<0,b>0,试作草图。
o
y
x
o
y
x
例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数y的值怎样变化?
o
x
1
2
3
4
-1
-2
-3
-4
1
1
2
3
4
-1
-2
y
解:
y= -2x+1
y =2x+1
x
0
-1/2
y =2x+1
1
0
x
0
1/2
y=-2x+1
1
0
(0,1)
(-1/2,0)
(1/2,0)
一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大;
y
x
一次函数y=kx+b (k?0)的性质:
当k<0时,y随x的增大而减小.
y
x
一次函数通常选取(0,b),
(-b/k,0)两点连线
一次函数 y = kx + b ( k ≠ 0 ) 有以下性质:
(1)当 k > 0 时,y 随 x 的增大而 。
(2)当 k < 0 时,y 随 x 的增大而 。
增大
减小
一次函数图象与性质
一次函数y=kx+b(b≠0)
图象
k,b的符号
经过象限
增减性
x
y
o
b
x
y
o
b
x
y
o
b
x
y
o
b
y随x的增
大而增大
y随x的增
大而增大
y随x的增
大而减少
y随x的增
大而减少
一、二、三
一、三、四
一、二、四
二、三、四
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
例、已知一次函数y=(m-1)x+2m+1。
(4)若图象经过一、二、四象限,
求m的取值范围。
解:由题意可知 k<0, b>0
m-1<0
2m+ 1 >0
m<1
m> -1/2
所以 -1/2 < m<1.
知识应用
练习:已知函数y=(m-2)x+n的
图象经过一、二、三象限.
求 : m、n的取值范围.
直线y=kx+b经过一、二、四象限,那么直线y=bx+k经过哪些象限?
思维拓展
3、直线y=-x-3经过___________象限
二、三、四
4、已知函数y=kx+2,且y随x的增大而增大,
则它的图象不经过第_____象限
四
考考你
5、一次函数y=kx+b,kb>0,且y随x的增大
而减小,则它的图象可能是 ( )
C
考考你
6、已知一次函数y=(a-1)x+b的图象如图所示,
那么a、b的取值范围是 ( )
A.a>1,b>0
B.a<1,b>0
C.a>1,b<0
D.a<1,b<0
A
考考你
y
x
0
(D)
y
x
0
(A )
y
x
0
( C )
y
x
0
(B)
逆向思维 小试牛刀
7、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
B
8、已知一次函数y = mx-(m-2),
若它的图象经过原点,则 m= ;
若点(0 ,3) 在它的图象上,则m = ;若它的图象经过一、二、四象限,则m .
2
-1
<0
9.对于一次函数y = mx-(m-2),若y 随x 的增大而增小,则其图象不
过 象限。
10.若直线 y = kx -3 过(2, 5),
则k = ;
若此直线平行于直线y = - 3x - 5,
则k= .
三
4
-3
D组:达标检测
1在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限
2已知一次函数y=x-2的大致图像为 ( )
A B C D
D
C
3.已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
(4)对于函数y=5x+6,k=__,b=__,y随x的增大而 ,反之y随x的减小而____.
增大
减小
5
6
(5)直线y=2x - 6与y轴的交点为 (_____),与x轴交于(_____)
0,-6
3, 0
6、 将函数y= - 2x的图象沿y轴向上平移
5个单位,得到的直线的解析式为
__________,图象经过第________
象限。
7、 将函数y= -0.5x的图象沿y轴向下平移
3个单位,得到的直线的解析式为
_________ ,图象经过第________
象限。
y= - 2x+5
一、二、四
y= -0.5x-3
二、三、四
8、函数y=(1-k)x中y随x的增大而减小,则k的范围是 .
k>1
9、直线y=-3x-6与x轴的交点坐标是 ,与y轴的交点坐标为 .
(-2,0)
(0,-6)
10、直线y=3x-1经过 象限;
一、三、四
11、若一次函数y=kx+b随x的增大y增大,且
kb>0,那么该直线不经过第 ————象限
四
12、直线y=kx+b的图象如图所示,确定k、b符号:
o
y
x
o
y
x
K<0,b>0
k>0,b<0
13、下图中哪一个是 y = x - 1的大致图像?
A
B
C
D
14、一次函数y=kx-k的图象可能是( )
A
B
C
D
C
15、已知一次函数y=(m-1)x+2m+1。
若图象平行于直线y=2x,求m的值
解:由题意可得 m – 1 = 2
所以 m = 3,
即y =(m-1)x+2m+1 = 2x + 7.
www.czsx.com.cn
16、已知一次函数y=(m-1)x+2m+1。
若图象交y轴于正半轴,求m的取值范围
解:
若图象交 y 轴于正半轴,
b>0,
2m+1>0
m-1≠0
m>-1/2
m≠1
所以 m>-1/2 且 m≠1。
1.设一次函数的一般形式y=kx+b(k≠0) ;
2.根据已知条件列出关于k , b 的二元一次方程组
3.解这个方程组,解出k, b ;
4 .将已经求出的 k, b的值代入所设解析式.
写出这个解析式
解题的步骤:
待定系数法:
像刚才这样先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,解出未知系数,从而得到所求结果的方法,叫做待定系数法.
1. 已知一次函数的图象如图所示,求该函数的解析式。
0 1 2 3 4 5 x
y
5
4
3
2
1
解:设这个一次函数的解析式为y=kx+b。
∴ b=3
3k+b=0
解方程组得 k=1
b=3
∴这个一次函数的解析式
为y= x+3。
(k≠0)从图中可以看出 图象过点(0,3)与(3,0)。
0 1 2 3 4 5 x
y
5
4
3
2
1
函数解析式y=kx+b(k≠0)
选取
解出
满足条件的两点(x1,y1)与(x2,y2)
一次函数的图象
直线
画出
选取
从数到形
从形到数
数学的思想方法:数形结合
x
0
y
-9
-4
B
A
3
5
由于两点确定了一条直线,即这个图象是一次函数y = kx+b
y = kx+b
A(3,5),
B(-4,-9)
解:因为图象是一次函数,所以设函数的解析式
为y = kx+b
且图象过点A(3,5)和点B(-4,-9),所以
由①-②得
∴这个函数的解析式为y = 2x-1
①
②
y
x
5
3
-4
-9
0
A
B
①
②
①
②
①
②
A
B
C
2.如图,一次函数的图象过点A且与正比例函数y=-x的图象交于点B。那么该一次函数的表达式为
-1 0 x
y=-x
2
A
B
y
y=x+2
若直线l与直线y= x-1关于x轴对称,则直线l的解析式为_____________。
1
2
y=- x+1
1
2
0 1 2 x
y
1
-1
A(2,0)
B(0,-1)
B1(0,1)
y= x-1
1
2
y=- x+1
1
2
总结:
若l直线与直线y = kx+b关于
(1)x轴对称,则直线l的解析式为 y = -kx-b,
即将 y 换成 –y 。
(2)y轴对称,则直线l的解析式为 y = -kx+b,
即将 x 换成 -x。
(3) 原点对称,则直线l的解析式为 y=kx-b,
即将y换成-y,x换成-x。
若直线l与直线y= x-1关于y轴对称,
则直线l的解析式为_____________。
想一想
若直线l与直线y= x-1关于原点对称,则直线l的解析式为_____________。
1
2
1
2
y=- x-1
1
2
y= x+1
1
2
例2 已知直线y=kx+b与直线y=2x平行且过点(-1,4),则k=___,b=___。
3.已知一次函数y=kx+b的图象与y=-3x+4的图象平行且与y轴相交于点(0,3)。则这个函数的解析式为__________________。
y=-3x+3
2
6
4.直线y=kx+b经过点A(-3,0)且与y轴交于点B,如果△AOB的(0为坐标原点)面积为4.5,则这条直线的解析式为( )。
A.y=x+3
B.y=-x-3
C.y=x+3或y=-x-3
D.y=x+3或y=x-3
·
(-3,0)
x
y
o
c
5、已知函数y=kx+b的图象经过点A(4,0),且与两坐标轴所围成的三角形的面积为6,则此函数的解析式为____________.
(4,0)
(0,3)
(0,-3)
A
B
B’
一次函数的图象与坐标轴所围成的面积问题,我们往往要进行分类讨论!
某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
①
②
解得
1.已知直线y=(2m-1)x+m与直线y=x-2平行,且与直线y= x+2n-3 交 y 轴于同一点,则m= ____, n=___.
2.如果要通过平移直线 得到 的图象,那么直线 必须向___平移___个 单位.
3.如果直线y =kx+b平行于直线y=2x+4,且与两坐标轴围成的三角形的面积为8,求直线y =kx+b 的解析式.
1、用待定系数法求一次函数的解析式。
2、数与形的关系----数形结合的思想。
课堂小结
3、对有些题目要分情况进行讨论——分类讨论的思想。
1、怎样的函数是一次函数?
一般地,形如y=kx+b(k,b是常数,k≠0)
的函数,叫做一次函数。
2、会区分一次函数与正比例函数
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数。
3、怎么画一次函数图像?
一次函数y=kx+b的图象是一条_____,我们称它为直线y=kx+b,它可以看作由________平移___个单位长度而得到
直线
直线y=kx
|b|
(当b>0时,向上平移;当b<0,向下平移)
平移法、描点法
4、一次函数y=kx+b的性质
5.用待定系数法求解析式
