人教版初中数学八年级下册 18.1.2《平行四边形的判定(二)》课件(共19张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册 18.1.2《平行四边形的判定(二)》课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:31:47 | ||
图片预览



文档简介
18.1.2
平行四边形的判定
平行四边形判定方法1
两组对边分别相等的四边形是平行四边形.
平行四边形判定方法2
两组对角分别相等的四边形是平行四边形.
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形
复习旧知
探究
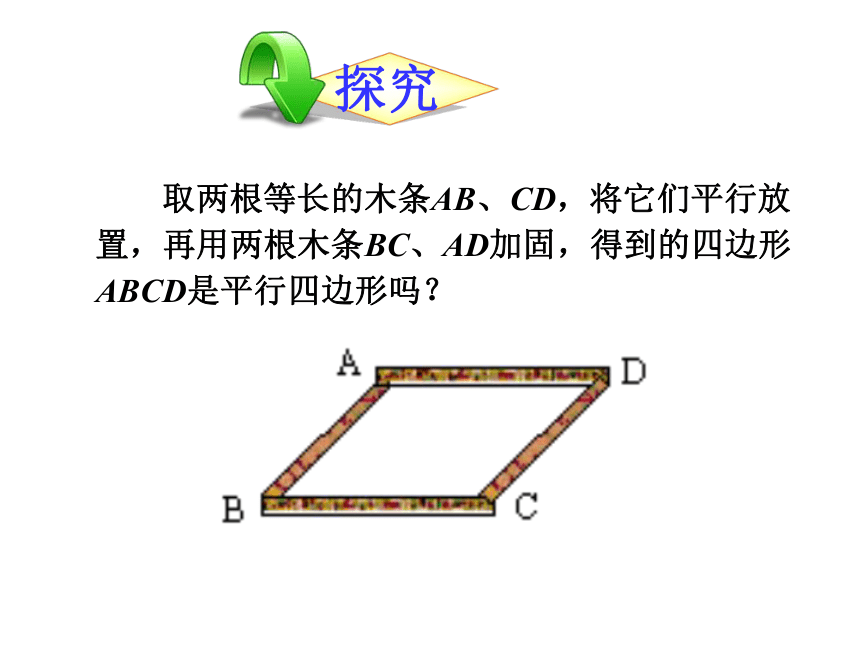
取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
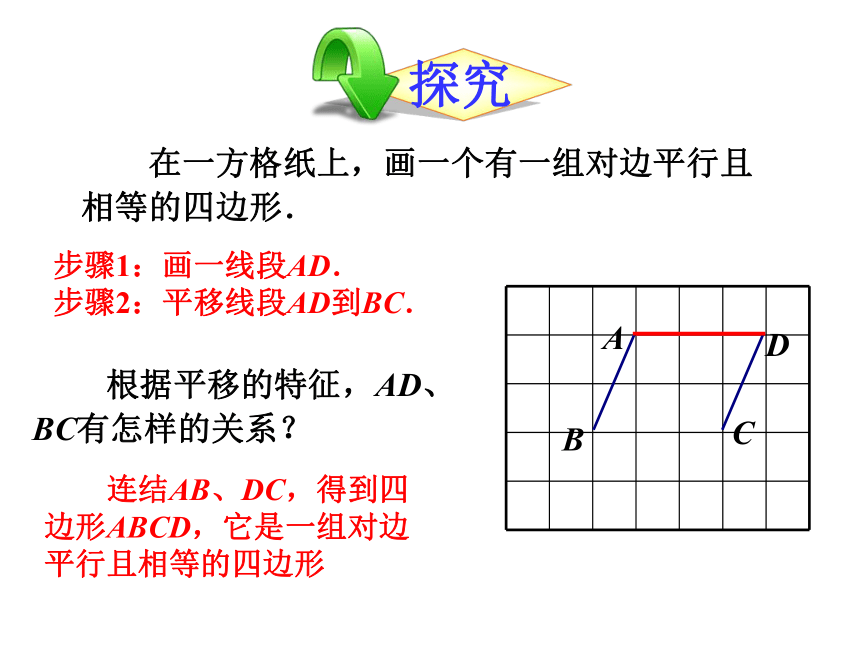
在一方格纸上,画一个有一组对边平行且相等的四边形.
步骤1:画一线段AD.
步骤2:平移线段AD到BC.
根据平移的特征,AD、BC有怎样的关系?
连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形
C
B
D
A
探究
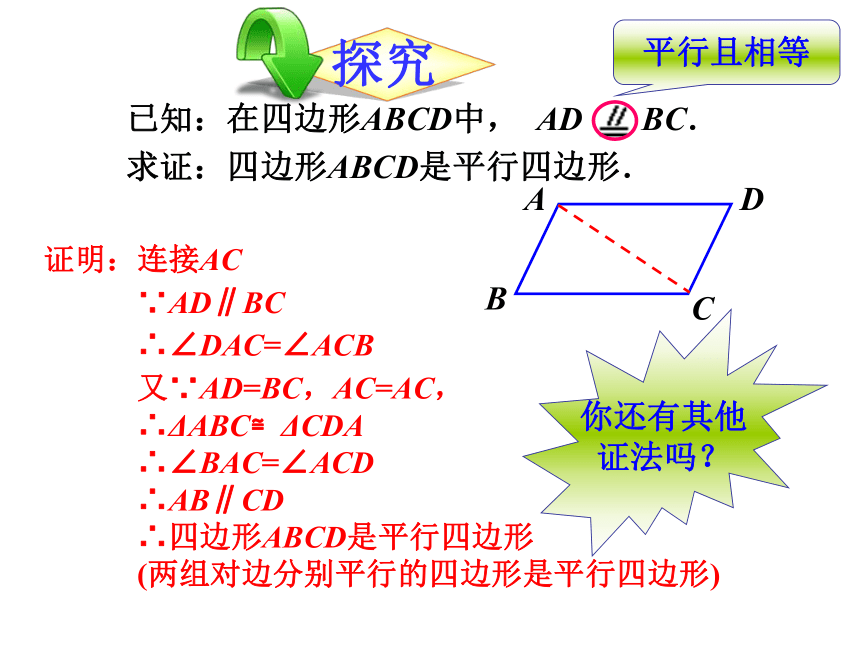
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
A
B
C
D
已知:在四边形ABCD中,
AD
BC.
求证:四边形ABCD是平行四边形.
平行且相等
你还有其他
证法吗?
探究
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
∵AB
CD
∴四边形ABCD是平行四边形.
A
B
C
D
知识要点
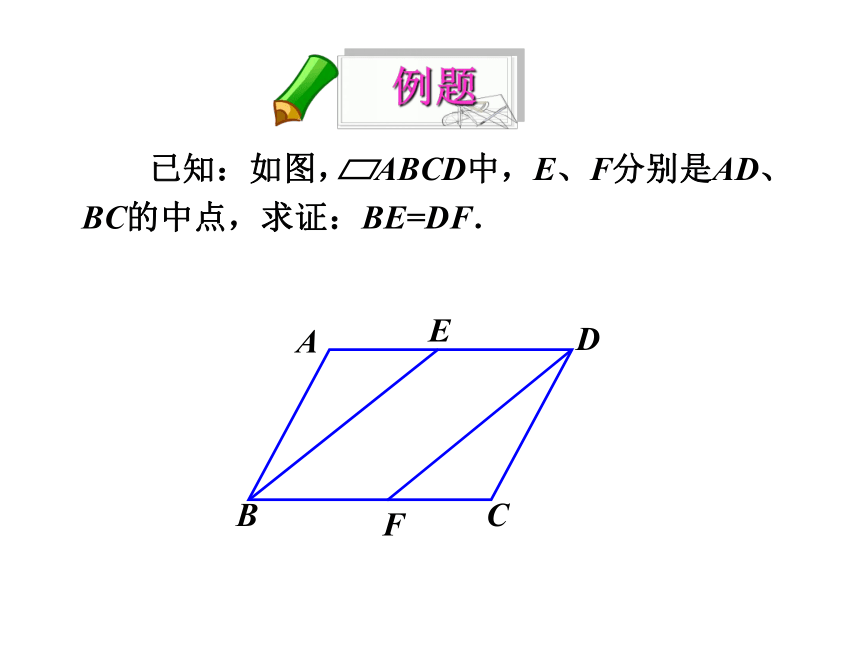
已知:如图,
ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.
例题
A
B
C
D
E
F
证明:∵
四边形ABCD是平行四边形,
∴
AD∥CB,AD=CD.
∵
E、F分别是AD、BC的中点,
∴
DE∥BF,
DE=BF.
∴
四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
∴
BE=DF.
A
B
C
D
E
F
在
ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有______个
.
抢答
A
B
C
D
E
F
G
H
6
练习
已知:如图,
ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
证明:∵
四边形ABCD是平行四边形,
∴
AB=CD,且AB∥CD.
∴
∠BAE=∠DCF.
∵
BE⊥AC于E,DF⊥AC于F,
∴
BE∥DF,且∠BEA=∠DFC=90°.
∴
△ABE≌△CDF
(AAS).
∴
BE=DF.
∴
四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
已知:如图,AC∥ED,点B在AC上,且AB=ED=BC,
找出图中的平行四边形,并说明理由.
四边形ABDE和四边形BCDE是平行四边形.
理由:一组对边平行且相等的四边形平行四边形.
A
B
C
E
D
小练习
已知:如图,在
ABCD中,AE、CF分别是
∠DAB、∠BCD的平分线.
求证:四边形AFCE是平行四边形.
提示:利用“一组对边平行且相等的四边形平行四边形”.
A
B
C
F
D
E
小练行四边形的判定方法
从边来判定
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
课堂小结
1.下列四边形哪些是平行四边形?为什么?
A
D
C
B
110°
70°
110°
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
随堂练习
2.根据下列条件,不能判定一个四边形为平行
四边形的是(
)
A.两组对边分别相等
B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行
C
3.如图四边形ABCD中,AB//CD,只需添加
一个条件,能使四边形ABCD是平行四边
形,现有条件:①AB=CD,②BC=AD,
③AD//BC,④∠ABC=∠ADC,
这些条件中,满足要求的有(
)
A.1个
B.2个
C.3个
D.4个
A
C
B
D
C
4.在下列条件中,不能判定四边形是平行四边形
的是(
)
A.AB∥CD,AD∥BC
B.
AB=CD,AD=BC
C.AB∥CD,AB=CD
D.
AB∥CD,AD=BC
D
C
B
D
O
A
5.如图,在
ABCD中,对角线AC,BD相交于点O,AC=10,BD=8,则AD长度的取值范围是
(
)
A.AD>1
B.AD<9
C.AD>10
D.1D
平行四边形的判定
平行四边形判定方法1
两组对边分别相等的四边形是平行四边形.
平行四边形判定方法2
两组对角分别相等的四边形是平行四边形.
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形
复习旧知
探究
取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
在一方格纸上,画一个有一组对边平行且相等的四边形.
步骤1:画一线段AD.
步骤2:平移线段AD到BC.
根据平移的特征,AD、BC有怎样的关系?
连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形
C
B
D
A
探究
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
A
B
C
D
已知:在四边形ABCD中,
AD
BC.
求证:四边形ABCD是平行四边形.
平行且相等
你还有其他
证法吗?
探究
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
∵AB
CD
∴四边形ABCD是平行四边形.
A
B
C
D
知识要点
已知:如图,
ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.
例题
A
B
C
D
E
F
证明:∵
四边形ABCD是平行四边形,
∴
AD∥CB,AD=CD.
∵
E、F分别是AD、BC的中点,
∴
DE∥BF,
DE=BF.
∴
四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
∴
BE=DF.
A
B
C
D
E
F
在
ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有______个
.
抢答
A
B
C
D
E
F
G
H
6
练习
已知:如图,
ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
证明:∵
四边形ABCD是平行四边形,
∴
AB=CD,且AB∥CD.
∴
∠BAE=∠DCF.
∵
BE⊥AC于E,DF⊥AC于F,
∴
BE∥DF,且∠BEA=∠DFC=90°.
∴
△ABE≌△CDF
(AAS).
∴
BE=DF.
∴
四边形BEDF是平行四边形(一组对边平行且相等的四边形平行四边形).
已知:如图,AC∥ED,点B在AC上,且AB=ED=BC,
找出图中的平行四边形,并说明理由.
四边形ABDE和四边形BCDE是平行四边形.
理由:一组对边平行且相等的四边形平行四边形.
A
B
C
E
D
小练习
已知:如图,在
ABCD中,AE、CF分别是
∠DAB、∠BCD的平分线.
求证:四边形AFCE是平行四边形.
提示:利用“一组对边平行且相等的四边形平行四边形”.
A
B
C
F
D
E
小练行四边形的判定方法
从边来判定
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
课堂小结
1.下列四边形哪些是平行四边形?为什么?
A
D
C
B
110°
70°
110°
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
随堂练习
2.根据下列条件,不能判定一个四边形为平行
四边形的是(
)
A.两组对边分别相等
B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行
C
3.如图四边形ABCD中,AB//CD,只需添加
一个条件,能使四边形ABCD是平行四边
形,现有条件:①AB=CD,②BC=AD,
③AD//BC,④∠ABC=∠ADC,
这些条件中,满足要求的有(
)
A.1个
B.2个
C.3个
D.4个
A
C
B
D
C
4.在下列条件中,不能判定四边形是平行四边形
的是(
)
A.AB∥CD,AD∥BC
B.
AB=CD,AD=BC
C.AB∥CD,AB=CD
D.
AB∥CD,AD=BC
D
C
B
D
O
A
5.如图,在
ABCD中,对角线AC,BD相交于点O,AC=10,BD=8,则AD长度的取值范围是
(
)
A.AD>1
B.AD<9
C.AD>10
D.1
