人教版初中数学七年级下册6.1.3《平方根》课件(共16张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册6.1.3《平方根》课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:18:44 | ||
图片预览






文档简介
第六章 实数
6.1 平方根 (第3课时)
复习旧知
求下列各数的算术平方根:
9,0,1.69,144,104,29,
一般地,一个正数x的平方等于a,即x2=a,那么这个正数x叫做a算术平方根。
算术平方根:
如果一个数的平方等于9,这个数是多少?
3是前面学习过的9的算术平方根,
-3与9有什么关系?
由于 ,
所以这个数是3或-3.
学习目标:
(1)掌握平方根的概念;
(2)能用符号正确表示一个数的平方根,
求某些非负数的平方根.
学习重点:
平方根的概念和求数的平方根.
根据上面的研究过程填表:
1.归纳平方根的概念
如果我们把 分别叫做
的平方根,你能类比算术
平方根的概念,给出平方根的概念吗?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说 如果 ,那么x 叫做a的平方根.
例如:3和-3是 9的平方根,
简记 是9的平方根.
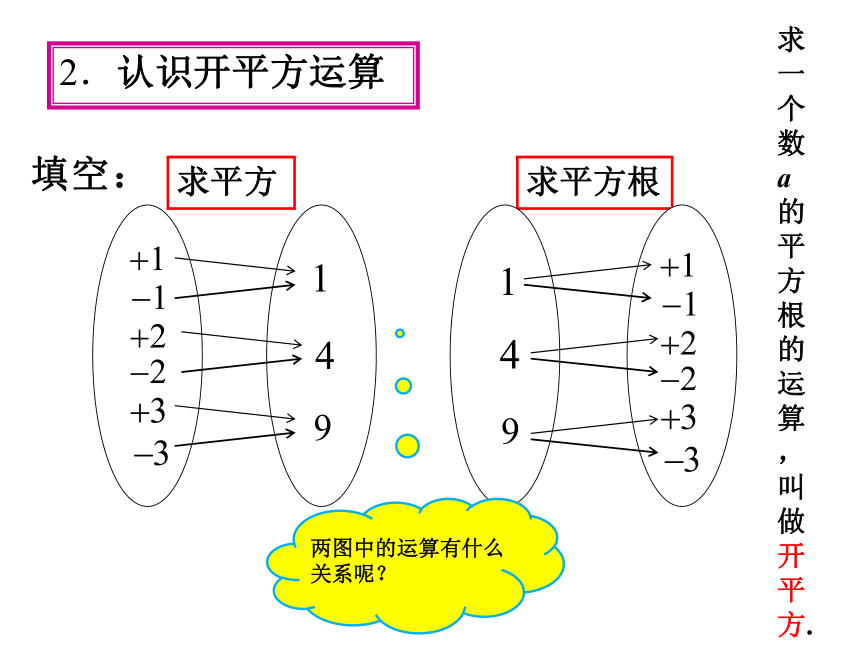
填空:
求平方
求平方根
2.认识开平方运算
两图中的运算有什么
关系呢?
求
一
个
数
a
的
平
方
根
的
运
算
,
叫
做
开
平
方.
例1 求下列各数的平方根:
解:(1)∵ ,
∴100的平方根是 10 .
即 .
解:(2) ∵
∴ 的平方根是 .
即 .
例2 判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是 ;
我们已经学过一个正数的算术平方根的表示方法,你能表示一个正数的平方根吗?
3.平方根的表示
正数a的算术平方根可以表示用 表示;
正数a的负的平方根,可以用符号 表示,
正数a的平方根用符号 表示.
读作“正、负根号a ”.
例3 判断下列各式计算是否正确,并说明理由.
例4 说出下列各式的意义,并求它们的值:
解:(1) ;
(2) ;
(3) .
4.思考
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
5.归纳小结
你能总结一下平方根与算术平方根的概念的区别与联系吗?
教科书 习题6.1第3、4、7、8题,
导学方案6.1平方根第三学时.
6.布置作业
6.1 平方根 (第3课时)
复习旧知
求下列各数的算术平方根:
9,0,1.69,144,104,29,
一般地,一个正数x的平方等于a,即x2=a,那么这个正数x叫做a算术平方根。
算术平方根:
如果一个数的平方等于9,这个数是多少?
3是前面学习过的9的算术平方根,
-3与9有什么关系?
由于 ,
所以这个数是3或-3.
学习目标:
(1)掌握平方根的概念;
(2)能用符号正确表示一个数的平方根,
求某些非负数的平方根.
学习重点:
平方根的概念和求数的平方根.
根据上面的研究过程填表:
1.归纳平方根的概念
如果我们把 分别叫做
的平方根,你能类比算术
平方根的概念,给出平方根的概念吗?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说 如果 ,那么x 叫做a的平方根.
例如:3和-3是 9的平方根,
简记 是9的平方根.
填空:
求平方
求平方根
2.认识开平方运算
两图中的运算有什么
关系呢?
求
一
个
数
a
的
平
方
根
的
运
算
,
叫
做
开
平
方.
例1 求下列各数的平方根:
解:(1)∵ ,
∴100的平方根是 10 .
即 .
解:(2) ∵
∴ 的平方根是 .
即 .
例2 判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是 ;
我们已经学过一个正数的算术平方根的表示方法,你能表示一个正数的平方根吗?
3.平方根的表示
正数a的算术平方根可以表示用 表示;
正数a的负的平方根,可以用符号 表示,
正数a的平方根用符号 表示.
读作“正、负根号a ”.
例3 判断下列各式计算是否正确,并说明理由.
例4 说出下列各式的意义,并求它们的值:
解:(1) ;
(2) ;
(3) .
4.思考
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
5.归纳小结
你能总结一下平方根与算术平方根的概念的区别与联系吗?
教科书 习题6.1第3、4、7、8题,
导学方案6.1平方根第三学时.
6.布置作业
