人教版初中数学七年级下册9.1.1《不等式及其解集》课件(共27张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册9.1.1《不等式及其解集》课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:37:29 | ||
图片预览







文档简介
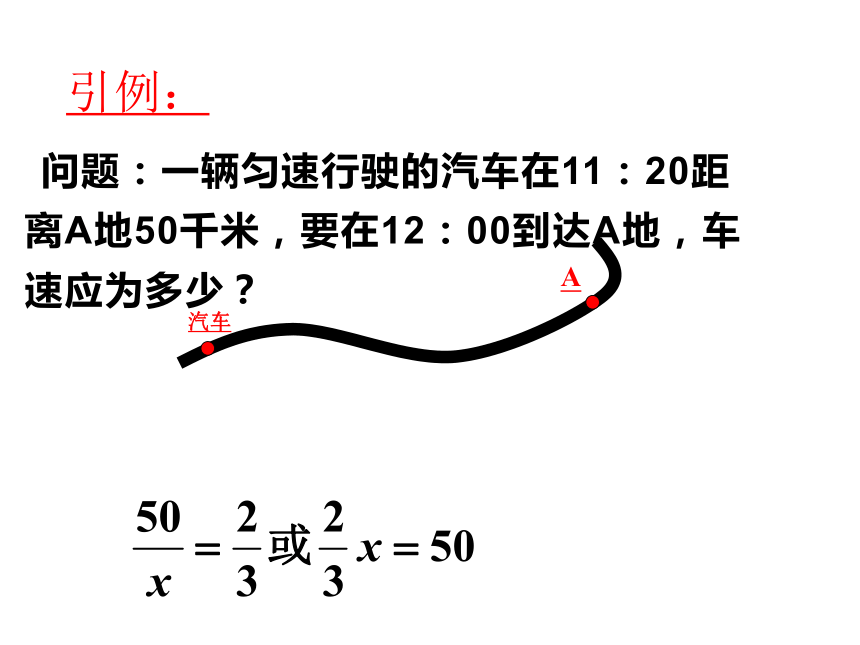
问题:一辆匀速行驶的汽车在11:20距离A地50千米,要在12:00到达A地,车速应为多少?
A
汽车
引例:
问题:一辆匀速行驶的汽车在11:20距离A地50千米,要在12:00之前驶过A地,车速应满足什么条件?
A
汽车
分析:设车速是x千米/时
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50千米所用的时间不到2/3小时,即
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶2/3小时的路程要超过50千米,即
一.不等式:
像 、 这样用“>”或“<”
表示大小关系的式子,叫做不等式.
不等式中常见的不等号有五种:
≠、>、<、≥、≤
(有无不等号判断不等式的关键,未知数?)
如:-3>-5,2≠6,x≤1等等都是不等式
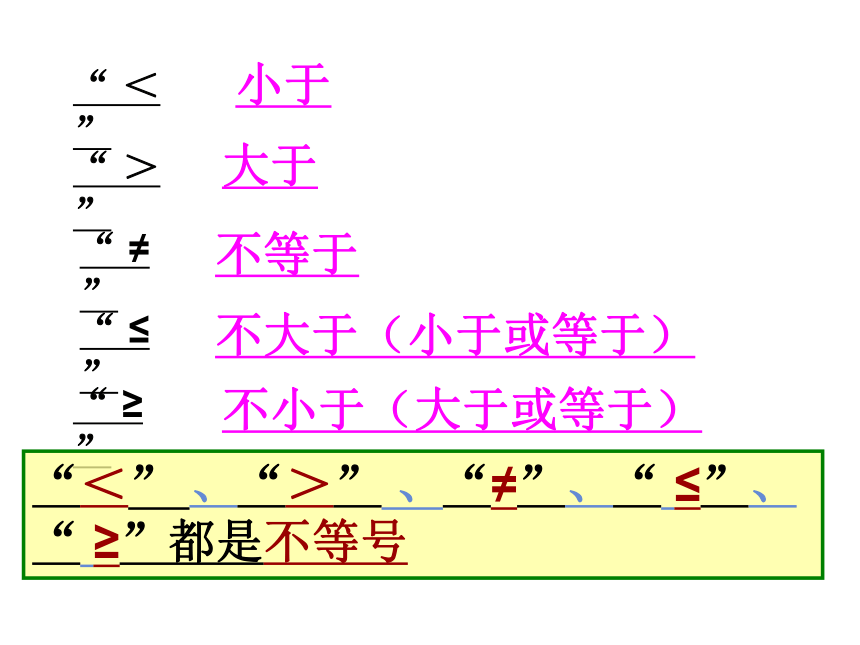
“ < ”
“ > ”
“ ≠ ”
“ ≤ ”
“ ≥ ”
小于
大于
不等于
不大于(小于或等于)
不小于(大于或等于)
“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
1、下列式子哪些是不等式?
① -1﹤3 ② -x+2=4
③ 3x ≠ 4y ④ 6 ﹥ 2
⑤ 2x -3 ⑥ 2m ﹤ n
是
不是
是
是
不是
是
1.用不等式表示下列关系:
(1)a与3的和是正数;
(2)m的倒数大于n的一半;
(3)a与b和的 是非正数 .
解:a+3>0;
解: > ;
解: (a+b)≤0
(4)x与5的差的3倍不是负数;
(5)m除以4的商不大于n与2的积
(6)a的相反数至少为1.
解:3(x-5)≥0;
解: ≤ 2n;
解:-a≥1.
随堂练习
P115 练习 1.用不等式表示:
(1)a是正数 (2)a是负数
(3)a与5的和小于7 (4)a与2的差大于-1
(5)a的4倍大于8 (6)a的一半小于3
与方程类似,我们可以把那些使不等式成立的未知数的值叫做不等式的解。
如:
二.不等式的解
76, 79, 80, 75.1, 90 不等式
的解 。这个不等式的解有无数个。
P116 练习
2.下列数值哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12,
一个含有未知数的不等式的所有解, 组成这个不等式的解集.
注意:不等式的解和不等式的解集是一样的吗?
练习:下列说法正确的是( )
A. x=3是2x>1的解 B. x=3是2x>1的唯一解
C. x=3不是2x>1的解 D. x=3是2x>1的解集
A
求不等式的解集的过程叫解不等式.
三.不等式的解集
解集:
前面学的方程组的解都只有一个,
今天所学不等式的解却不止一个.
不等式的解集的概念:一个含有未知数的不等式的所有解组成的集合,简称这个不等式的解集.
求这个不等式的解集的过程叫做解不等式。
不等式解集的表示方法
第一种:用不等式(如x>2),即用最简形式的不等式(如x>a或x第二种:用数轴,标出数轴上某一区间,区间内的点对应的数值都是不等式的解.
P115 练习3:直接说出不等式的解集:
⑴ x+3>6 ⑵ 2x<8 ⑶ x-2>0
解: ⑴ x>3 ;
⑵ x<4 ;
⑶ x>2.
这就是用不等式法表示不等式的解集
例题: 用数轴表示下列不等式的解集:
⑴ x>-1; ⑵ x≥ -1; ⑶ x< -1; ⑷ x≤ -1.
解:
○
0
-1
⑴
●
0
-1
⑵
○
0
-1
⑶
●
0
-1
⑷
总结: ①用数轴表示不等式的解集的步骤:
1:画数轴;
2:找界点;
3:定方向.
②用数轴表示不等式的解集,应记住的规律:
大于向右画, 小于向左画;
有等号(≥ ,≤)画实心点,无等号(>,<)画空心圆.
1、不等式3x>5的解集是:_________
A
5
x >
3
2、在数轴上表示不等式3x>5的解集,正确的是( )
(A)
1
2
5
3
0
1
2
(B)
(D)
5
3
0
1
2
5
3
0
1
2
5
3
0
(C)
4、请直接说出下列不等式的解集, 并在数轴上表示。
(1) 2x<8 (2)x-2>0
x>2
0
1
2
0
1
2
3
4
x<4
找点
定向
画线
○
0
-3
⑴
○
0
-3
⑶
●
0
2
⑵
●
0
a
⑷
试一试:
1、写出下列数轴所表示的不等式的解集:
X > -3
X ≥ 2
X < -3
X ≤ a
2.(填空)某市二月某一天的最低气温是-2,最高气温是9。如果设这天气温为t(℃),那么t满足的条件是 .
-2≤t≤9
课堂小结
不等式的解、不等式的解集;
解不等式的有关概念;
在数轴上表示不等式的解集.
用数轴表示不等式的解集
不等式的解集一般来说有以下四种情况:
(1) X > a
(2) X < a
(3) X ≥ a
(4) X ≤ a
a
a
.
a
a
.
步骤:画数轴,定界点,定方向
大于往右走,小于往左走
作业
课本120页 2、3题
个98
A
汽车
引例:
问题:一辆匀速行驶的汽车在11:20距离A地50千米,要在12:00之前驶过A地,车速应满足什么条件?
A
汽车
分析:设车速是x千米/时
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50千米所用的时间不到2/3小时,即
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶2/3小时的路程要超过50千米,即
一.不等式:
像 、 这样用“>”或“<”
表示大小关系的式子,叫做不等式.
不等式中常见的不等号有五种:
≠、>、<、≥、≤
(有无不等号判断不等式的关键,未知数?)
如:-3>-5,2≠6,x≤1等等都是不等式
“ < ”
“ > ”
“ ≠ ”
“ ≤ ”
“ ≥ ”
小于
大于
不等于
不大于(小于或等于)
不小于(大于或等于)
“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
1、下列式子哪些是不等式?
① -1﹤3 ② -x+2=4
③ 3x ≠ 4y ④ 6 ﹥ 2
⑤ 2x -3 ⑥ 2m ﹤ n
是
不是
是
是
不是
是
1.用不等式表示下列关系:
(1)a与3的和是正数;
(2)m的倒数大于n的一半;
(3)a与b和的 是非正数 .
解:a+3>0;
解: > ;
解: (a+b)≤0
(4)x与5的差的3倍不是负数;
(5)m除以4的商不大于n与2的积
(6)a的相反数至少为1.
解:3(x-5)≥0;
解: ≤ 2n;
解:-a≥1.
随堂练习
P115 练习 1.用不等式表示:
(1)a是正数 (2)a是负数
(3)a与5的和小于7 (4)a与2的差大于-1
(5)a的4倍大于8 (6)a的一半小于3
与方程类似,我们可以把那些使不等式成立的未知数的值叫做不等式的解。
如:
二.不等式的解
76, 79, 80, 75.1, 90 不等式
的解 。这个不等式的解有无数个。
P116 练习
2.下列数值哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12,
一个含有未知数的不等式的所有解, 组成这个不等式的解集.
注意:不等式的解和不等式的解集是一样的吗?
练习:下列说法正确的是( )
A. x=3是2x>1的解 B. x=3是2x>1的唯一解
C. x=3不是2x>1的解 D. x=3是2x>1的解集
A
求不等式的解集的过程叫解不等式.
三.不等式的解集
解集:
前面学的方程组的解都只有一个,
今天所学不等式的解却不止一个.
不等式的解集的概念:一个含有未知数的不等式的所有解组成的集合,简称这个不等式的解集.
求这个不等式的解集的过程叫做解不等式。
不等式解集的表示方法
第一种:用不等式(如x>2),即用最简形式的不等式(如x>a或x
P115 练习3:直接说出不等式的解集:
⑴ x+3>6 ⑵ 2x<8 ⑶ x-2>0
解: ⑴ x>3 ;
⑵ x<4 ;
⑶ x>2.
这就是用不等式法表示不等式的解集
例题: 用数轴表示下列不等式的解集:
⑴ x>-1; ⑵ x≥ -1; ⑶ x< -1; ⑷ x≤ -1.
解:
○
0
-1
⑴
●
0
-1
⑵
○
0
-1
⑶
●
0
-1
⑷
总结: ①用数轴表示不等式的解集的步骤:
1:画数轴;
2:找界点;
3:定方向.
②用数轴表示不等式的解集,应记住的规律:
大于向右画, 小于向左画;
有等号(≥ ,≤)画实心点,无等号(>,<)画空心圆.
1、不等式3x>5的解集是:_________
A
5
x >
3
2、在数轴上表示不等式3x>5的解集,正确的是( )
(A)
1
2
5
3
0
1
2
(B)
(D)
5
3
0
1
2
5
3
0
1
2
5
3
0
(C)
4、请直接说出下列不等式的解集, 并在数轴上表示。
(1) 2x<8 (2)x-2>0
x>2
0
1
2
0
1
2
3
4
x<4
找点
定向
画线
○
0
-3
⑴
○
0
-3
⑶
●
0
2
⑵
●
0
a
⑷
试一试:
1、写出下列数轴所表示的不等式的解集:
X > -3
X ≥ 2
X < -3
X ≤ a
2.(填空)某市二月某一天的最低气温是-2,最高气温是9。如果设这天气温为t(℃),那么t满足的条件是 .
-2≤t≤9
课堂小结
不等式的解、不等式的解集;
解不等式的有关概念;
在数轴上表示不等式的解集.
用数轴表示不等式的解集
不等式的解集一般来说有以下四种情况:
(1) X > a
(2) X < a
(3) X ≥ a
(4) X ≤ a
a
a
.
a
a
.
步骤:画数轴,定界点,定方向
大于往右走,小于往左走
作业
课本120页 2、3题
个98
