人教版九年级数学下册27.2.2相似三角形的性质教学课件 (共18张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.2.2相似三角形的性质教学课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1011.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
27.2.2 相似三角形的性质
学习目标
1.掌握相似三角形的性质定理.
2.掌握综合运用相似三角形的判定定理和性质定理来解决问题.
3.进一步体验类比的学习思想.
4.通过相似性质的学习,感受图形和语言的和谐美
1.什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
2.如何判定两个三角形相似?
①定义;
②预备定理(平行);
③三边成比例;
④两角分别相等;
⑤两边成比例且夹角相等;
温故知新
全等三角形与相似三角形性质比较
全等三角形
相似三角形
对应边相等
对应边的比相等
对应角相等
对应角相等
对应高相等
对应高的比?
对应中线相等
对应中线的比?
对应角平分线相等
对应角平分线的比?
周长相等
周长的比?
面积相等
面积的比?
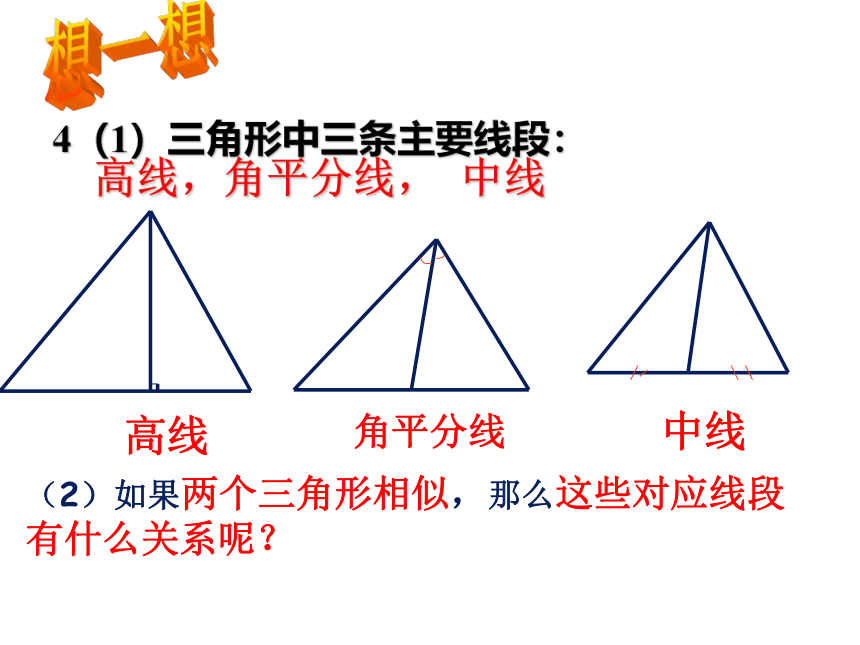
4(1)三角形中三条主要线段:
高线,角平分线, 中线
高线
角平分线
中线
(2)如果两个三角形相似,那么这些对应线段有什么关系呢?
∴
∵ △ABC∽ ,
解
△
∴ ∠B =∠
又 ∠AHB =∠ = 90°,
∴ △ABH∽
△
动脑筋
如图,已知△ABC∽△ , AH、 分
别为对应边BC, 上的高,那么 吗?
类似地,我们可以得到其余两组对应边上的高的比也等于相似比.
由此得到相似三角形的性质:
相似三角形对应高的比等于相似比.
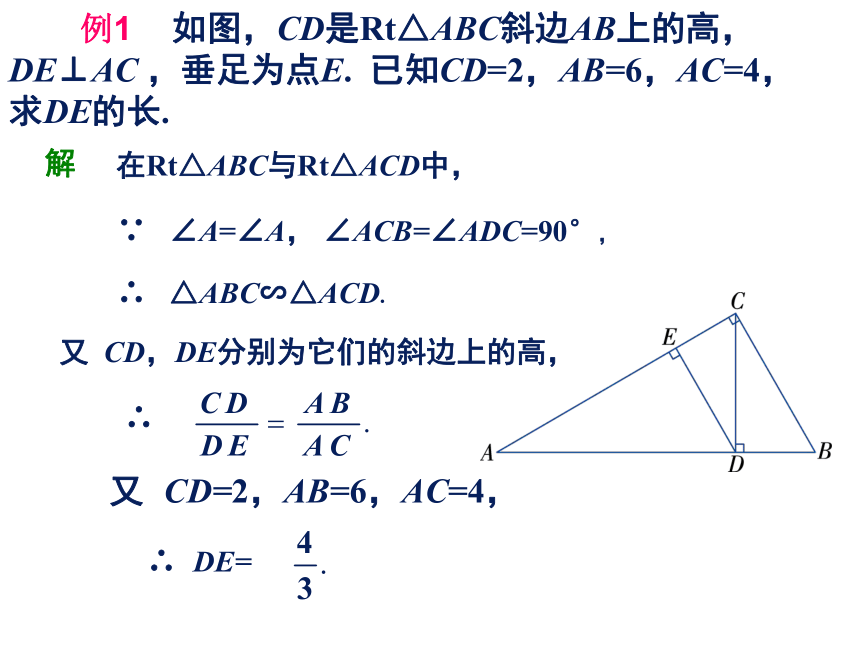
∵ ∠A=∠A, ∠ACB=∠ADC=90°,
在Rt△ABC与Rt△ACD中,
解
∴ △ABC∽△ACD.
又 CD,DE分别为它们的斜边上的高,
∴
又 CD=2,AB=6,AC=4,
∴ DE=
例1 如图,CD是Rt△ABC斜边AB上的高, DE⊥AC ,垂足为点E. 已知CD=2,AB=6,AC=4,求DE的长.
已知△ABC∽△ , 若AD、 分别为
, 的中线,那么 成立吗?
由此你能得出什么结论?
△ABC
△
议一议
议一议
议一议
由此得到相似三角形的性质:
相似三角形对应中线的比等于相似比.
∴ ∠B=∠ , ∠BAC=∠ .
又AT、 分别为对应角∠BAC,∠
的角平分线,
∠
=
=
∠
∴ ∠BAT=
∠BAC
∴
△ABT ∽△
∴
例2 如图,已知△ABC∽△ , AT、 分别为
对应角∠BAC,∠ 的角平分线.
求证:
类似地,我们可以得到另外两组对应角平分线
的比也等于相似比.
相似三角形对应角平分线的比等于相似比.
由此得到相似三角形的性质:
证明:∵△ABC∽△A'B'C'
那么
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,设
┓
┓
相似三角形对应高的比等于对应边的比.
结论:
你能有条理地表达理由吗?
' '
AB
k
A B
=
一:
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于对应边的比.
结论:
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的角平分线,设
你能有条理地表达理由吗?
' '
AB
k
A B
=
二:
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,设
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于对应边的比.
结论:
你能有条理地表达理由吗?
' '
AB
k
A B
=
三:
A'
B'
C'
A
B
C
相似三角形周长的比等于对应边的比.
结论:
已知:△ABC∽△A'B'C'
你能有条理地表达 理由吗?
?
' '
AB
k
A B
=
设:
四:
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,设
┓
┓
相似三角形面积之比等于对应边的比的平方.
结论:
你能有条理地表达理由吗?
?
' '
AB
k
A B
=
五:
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于
相似三角形的性质
归纳小结
相似比
练习
已知△ABC∽△DEF, AM,DN 分别△ABC,
△DEF 的一条中线,且AM= 6cm, AB= 8cm,
DE= 4cm,求DN的长.
1.
∴ DN=3(cm).
又 AM,DN分别为BC,EF边上的中线,
∴
∵ △ABC∽△DEF,
解
即
∵
解
△ABC ∽
△
即
∴
∴ =4.5.
如图, ,AD,BE 分别是
△ABC 的高和中线, , 分别是
的高和中线 ,且 AD = 4, = 3,BE= 6,
求 的长.
2.
△ABC ∽
△
△
自我挑战
如图,△ABC为锐角三角形,AD是边BC边上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上。已知BC=30㎝,AD=20㎝,求这个正方形的边长。
学习目标
1.掌握相似三角形的性质定理.
2.掌握综合运用相似三角形的判定定理和性质定理来解决问题.
3.进一步体验类比的学习思想.
4.通过相似性质的学习,感受图形和语言的和谐美
1.什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
2.如何判定两个三角形相似?
①定义;
②预备定理(平行);
③三边成比例;
④两角分别相等;
⑤两边成比例且夹角相等;
温故知新
全等三角形与相似三角形性质比较
全等三角形
相似三角形
对应边相等
对应边的比相等
对应角相等
对应角相等
对应高相等
对应高的比?
对应中线相等
对应中线的比?
对应角平分线相等
对应角平分线的比?
周长相等
周长的比?
面积相等
面积的比?
4(1)三角形中三条主要线段:
高线,角平分线, 中线
高线
角平分线
中线
(2)如果两个三角形相似,那么这些对应线段有什么关系呢?
∴
∵ △ABC∽ ,
解
△
∴ ∠B =∠
又 ∠AHB =∠ = 90°,
∴ △ABH∽
△
动脑筋
如图,已知△ABC∽△ , AH、 分
别为对应边BC, 上的高,那么 吗?
类似地,我们可以得到其余两组对应边上的高的比也等于相似比.
由此得到相似三角形的性质:
相似三角形对应高的比等于相似比.
∵ ∠A=∠A, ∠ACB=∠ADC=90°,
在Rt△ABC与Rt△ACD中,
解
∴ △ABC∽△ACD.
又 CD,DE分别为它们的斜边上的高,
∴
又 CD=2,AB=6,AC=4,
∴ DE=
例1 如图,CD是Rt△ABC斜边AB上的高, DE⊥AC ,垂足为点E. 已知CD=2,AB=6,AC=4,求DE的长.
已知△ABC∽△ , 若AD、 分别为
, 的中线,那么 成立吗?
由此你能得出什么结论?
△ABC
△
议一议
议一议
议一议
由此得到相似三角形的性质:
相似三角形对应中线的比等于相似比.
∴ ∠B=∠ , ∠BAC=∠ .
又AT、 分别为对应角∠BAC,∠
的角平分线,
∠
=
=
∠
∴ ∠BAT=
∠BAC
∴
△ABT ∽△
∴
例2 如图,已知△ABC∽△ , AT、 分别为
对应角∠BAC,∠ 的角平分线.
求证:
类似地,我们可以得到另外两组对应角平分线
的比也等于相似比.
相似三角形对应角平分线的比等于相似比.
由此得到相似三角形的性质:
证明:∵△ABC∽△A'B'C'
那么
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,设
┓
┓
相似三角形对应高的比等于对应边的比.
结论:
你能有条理地表达理由吗?
' '
AB
k
A B
=
一:
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于对应边的比.
结论:
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的角平分线,设
你能有条理地表达理由吗?
' '
AB
k
A B
=
二:
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,设
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于对应边的比.
结论:
你能有条理地表达理由吗?
' '
AB
k
A B
=
三:
A'
B'
C'
A
B
C
相似三角形周长的比等于对应边的比.
结论:
已知:△ABC∽△A'B'C'
你能有条理地表达 理由吗?
?
' '
AB
k
A B
=
设:
四:
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,设
┓
┓
相似三角形面积之比等于对应边的比的平方.
结论:
你能有条理地表达理由吗?
?
' '
AB
k
A B
=
五:
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于
相似三角形的性质
归纳小结
相似比
练习
已知△ABC∽△DEF, AM,DN 分别△ABC,
△DEF 的一条中线,且AM= 6cm, AB= 8cm,
DE= 4cm,求DN的长.
1.
∴ DN=3(cm).
又 AM,DN分别为BC,EF边上的中线,
∴
∵ △ABC∽△DEF,
解
即
∵
解
△ABC ∽
△
即
∴
∴ =4.5.
如图, ,AD,BE 分别是
△ABC 的高和中线, , 分别是
的高和中线 ,且 AD = 4, = 3,BE= 6,
求 的长.
2.
△ABC ∽
△
△
自我挑战
如图,△ABC为锐角三角形,AD是边BC边上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上。已知BC=30㎝,AD=20㎝,求这个正方形的边长。
