6.3实数 课件(共19张PPT)
图片预览






文档简介
------从有理数扩展到实数
我国古代数学家关于π的研究. 圆的周长与直径的比值是一个常数π,它是一个无理数,我国古代数学家早已作出了巨大的贡献。
在东汉初年的数学书《 周髀算经》里已经载有“周三径一”,称之为“古率”,就是说,直径是1的圆,它的周长是3.
西汉末年,刘歆(约分元前50年到公元23年)定圆周率为3.1547,
东汉时代,张衡(公元78-139年)求得约等于3.1622.(印度数学家罗笈多提出的圆周率,已迟于张衡500多年.)
三国时,魏人刘徽(公元263年)创立了求圆周率的准确值的原理,他用割圆术求得圆周率的前三位数字是π≈3.14?,称为徽率.
南北朝时代的祖冲之(公元429年—500年),他已推算出 3.1415926<π<3.1415927. 也就是π≈3.1415926?,他是世界上第一个确定圆周率准确到7位小数的人.祖冲之又提出了用两个分数表示π的近似值.即22 :7及355 :113,分别称为π的约率和密度. 在祖冲之发现密率一千多年后,欧洲的安托尼兹(16世纪~17世纪)才重新发现了这个值.
圆周率的历史
1
理解实数的概念,熟练对实数进行分类。
2
探索实数与数轴的关系。
3
学会在实数范围内求相反数、绝对值。
自主学习1、实数的概念与分类
⑴说一说:下列各数中
0 1.414
0.1010010001…
有理数: 。
无理数: 。
归 纳: 和 统称为实数。
0
1.414
0.1010010001…
有理数
无理数
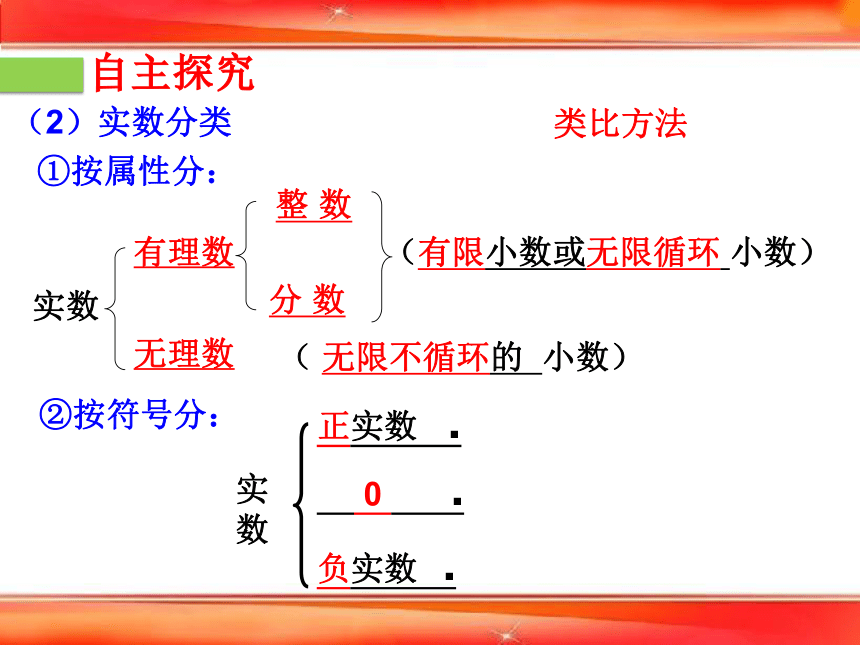
(2)实数分类
①按属性分:
实数
有理数
(有限小数或无限循环 小数)
( 无限不循环的 小数)
无理数
整 数
分 数
类比方法
实数
正实数 .
0 .
负实数 .
②按符号分:
(1) 的相反数是 。
自主学习2、实数范围内数的相反数、绝对值
(2)实数的绝对值的性质:
只有符号不同的两个实数互为相反数 。
(a>0)
(a=0)
(a<0)
a
- a
0
(1)探究设计:
①利用两个边长为1个单位长度的正方形剪拼成一个面积为2 个平方单位长度的正方形。
②拼剪成的新正方形边长是 个单位长度。
③在数轴上标出 和 所在的点。
思考:如何在数轴上标出无理数 和 这两个点?
探究活动: 实数和数轴的关系
正方形,
新正方形的边长是_____
0
1
-1
√2
如图是两个边长1的正方形
拼成的长方形, 其面积是2.
现剪下两个角重新拼成一个
√2
√2
2
√2
下图数轴中, 正方形的对角线长
为____,
以原点为圆心, 对角线长为
√2
半径画弧截得一点,
该点
与原点的距离是____,
√2
该点表示的数是____.
√2
√2
-
活动过程
实数与数轴上的点是一一对应关系.
逆向思维
活动过程
(2)变式探索:你能否在数轴上标出无理数 这个点?
a
b
c
勾股定理:a2+b2=c2
1
…
(3) 你从探究活动中得到了什么结论?
(一)把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
0,
(1)负实数集合( )
(2)有理数集合( )
(3)无理数集合( )
(二)求下列各数相反数和绝对值。
(一)组内展示巩固提升内容
(二)小结梳理
你还有什么困惑?
你收获了什么?
…
实数
课堂小结
…
有理数
…
无理数
★实数和数轴上的点是一一对应的.
1、把下列各数填入相应的集合
无理数集合
有理数集合
2、填空题
3、判断(正确的画“ ”,错误的画“ ”)
(1)任何一个无理数的绝对值都是正数。( )
(2)带根号的数都是无理数。 ( )
(3)实数可以分为正实数和负实数两类。( )
4、若将下列三个数 表示在数轴上,其
中能被如图所示的墨渍覆盖的数是( )
-2
0
2
1
3
4
-1
5、在已知实数a,b,c在数轴上的位置如下图所示
0
b
c
a
试化简:
变式一:
变式二:
问题:无理数 能在数轴上表示出来吗?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
活动过程
我国古代数学家关于π的研究. 圆的周长与直径的比值是一个常数π,它是一个无理数,我国古代数学家早已作出了巨大的贡献。
在东汉初年的数学书《 周髀算经》里已经载有“周三径一”,称之为“古率”,就是说,直径是1的圆,它的周长是3.
西汉末年,刘歆(约分元前50年到公元23年)定圆周率为3.1547,
东汉时代,张衡(公元78-139年)求得约等于3.1622.(印度数学家罗笈多提出的圆周率,已迟于张衡500多年.)
三国时,魏人刘徽(公元263年)创立了求圆周率的准确值的原理,他用割圆术求得圆周率的前三位数字是π≈3.14?,称为徽率.
南北朝时代的祖冲之(公元429年—500年),他已推算出 3.1415926<π<3.1415927. 也就是π≈3.1415926?,他是世界上第一个确定圆周率准确到7位小数的人.祖冲之又提出了用两个分数表示π的近似值.即22 :7及355 :113,分别称为π的约率和密度. 在祖冲之发现密率一千多年后,欧洲的安托尼兹(16世纪~17世纪)才重新发现了这个值.
圆周率的历史
1
理解实数的概念,熟练对实数进行分类。
2
探索实数与数轴的关系。
3
学会在实数范围内求相反数、绝对值。
自主学习1、实数的概念与分类
⑴说一说:下列各数中
0 1.414
0.1010010001…
有理数: 。
无理数: 。
归 纳: 和 统称为实数。
0
1.414
0.1010010001…
有理数
无理数
(2)实数分类
①按属性分:
实数
有理数
(有限小数或无限循环 小数)
( 无限不循环的 小数)
无理数
整 数
分 数
类比方法
实数
正实数 .
0 .
负实数 .
②按符号分:
(1) 的相反数是 。
自主学习2、实数范围内数的相反数、绝对值
(2)实数的绝对值的性质:
只有符号不同的两个实数互为相反数 。
(a>0)
(a=0)
(a<0)
a
- a
0
(1)探究设计:
①利用两个边长为1个单位长度的正方形剪拼成一个面积为2 个平方单位长度的正方形。
②拼剪成的新正方形边长是 个单位长度。
③在数轴上标出 和 所在的点。
思考:如何在数轴上标出无理数 和 这两个点?
探究活动: 实数和数轴的关系
正方形,
新正方形的边长是_____
0
1
-1
√2
如图是两个边长1的正方形
拼成的长方形, 其面积是2.
现剪下两个角重新拼成一个
√2
√2
2
√2
下图数轴中, 正方形的对角线长
为____,
以原点为圆心, 对角线长为
√2
半径画弧截得一点,
该点
与原点的距离是____,
√2
该点表示的数是____.
√2
√2
-
活动过程
实数与数轴上的点是一一对应关系.
逆向思维
活动过程
(2)变式探索:你能否在数轴上标出无理数 这个点?
a
b
c
勾股定理:a2+b2=c2
1
…
(3) 你从探究活动中得到了什么结论?
(一)把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
0,
(1)负实数集合( )
(2)有理数集合( )
(3)无理数集合( )
(二)求下列各数相反数和绝对值。
(一)组内展示巩固提升内容
(二)小结梳理
你还有什么困惑?
你收获了什么?
…
实数
课堂小结
…
有理数
…
无理数
★实数和数轴上的点是一一对应的.
1、把下列各数填入相应的集合
无理数集合
有理数集合
2、填空题
3、判断(正确的画“ ”,错误的画“ ”)
(1)任何一个无理数的绝对值都是正数。( )
(2)带根号的数都是无理数。 ( )
(3)实数可以分为正实数和负实数两类。( )
4、若将下列三个数 表示在数轴上,其
中能被如图所示的墨渍覆盖的数是( )
-2
0
2
1
3
4
-1
5、在已知实数a,b,c在数轴上的位置如下图所示
0
b
c
a
试化简:
变式一:
变式二:
问题:无理数 能在数轴上表示出来吗?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
活动过程
