人教版数学八年级下册 20.2 方差 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级下册 20.2 方差 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:28:34 | ||
图片预览







文档简介
怎样才能衡量整个一
组数据的波动大小呢?
数据的波动程度(1)
1、理解方差概念的产生和形成的过程。会用方差计算公式来比较两组数据的波动大小。
2、培养学生的统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义。
重点:方差产生的必要性和应用方差公式解决实际问题。
难点:理解方差公式,应用方差对数据波动情况的比较、判断。
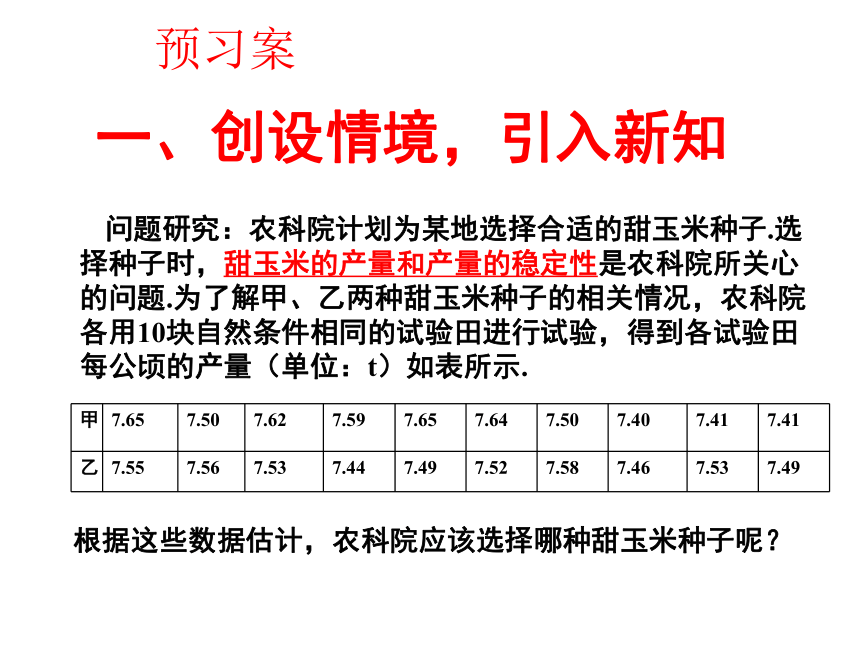
一、创设情境,引入新知
问题研究:农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如表所示.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
预习案
甲、乙两种甜玉米的平均产量相差不大,由此可以估计出这个地区种植这两种甜玉米,它们的平均产量相差不大.
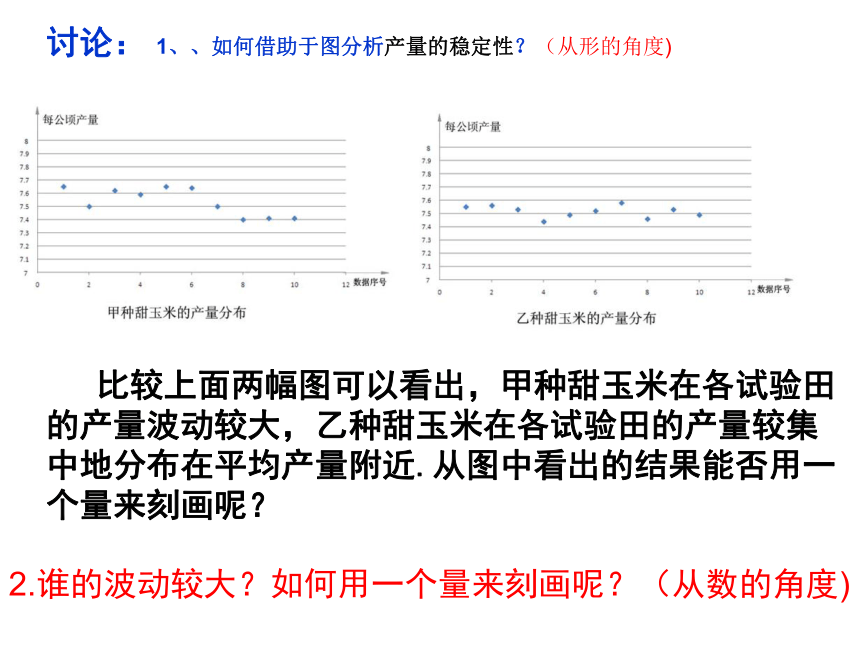
比较上面两幅图可以看出,甲种甜玉米在各试验田的产量波动较大,乙种甜玉米在各试验田的产量较集中地分布在平均产量附近.从图中看出的结果能否用一个量来刻画呢?
讨论: 1、、如何借助于图分析产量的稳定性?(从形的角度)
2.谁的波动较大?如何用一个量来刻画呢?(从数的角度)
二、理解概念,完善新知
探究案
方差定义
设有n个数据x1,x2,…,xn中,各数据与它们的平均数的差的平方分别是(x1-x)2,(x2-x)2 ,… (xn-x)2 ,那么我们用它们的平均数,即用
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作S2.
由此可知,乙种甜玉米的产量比较稳定,
可以推测,这个地区比较适合种植乙种甜玉米.
讨论:
(1)数据分散(即数据在平均数附近波动较大)时,方差值怎样?
(2)数据集中时,方差值怎样?
(3)方差大小与数据波动性大小有怎样的关系?
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差越大,数据的波动越____;
方差越小,数据的波动越____.
大
小
(4)如何计算一组数据的方差?
第一步:先求平均数;
第二步:再用方差公式计算。
三、解决问题,应用新知
问题1:在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如表所示.
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
解:甲、乙两团演员的平均身高分别是:
由 可知:甲芭蕾舞团女演员的身高更整齐。
方差分别是:
1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的。
(1)6 6 6 6 6 6 6
四 巩固新知
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
巩固新知
2、下列统计量中,能反映一名同学在7—9年级学段
的学习成绩稳定程度的是( )
A、平均数 B、中位数 C、众数 D、方差
3、如果样本方差
那么这个样本的平均数为_____,样本容量为
_____.
D
2
4
巩固新知
4、一组数据:-2,-1,0,x,1的平均数是0,则
X=_____,方差S2=______.
5、为了考察,甲、乙两种小麦的长势,分别从中抽
出20株测得其高度,并求得它们的方差分别为:
则____种小麦的长势比较整齐.
2
2
甲
五 课堂小结
你本节课学到了什么?
1.如何计算一组数据的方差?
第一步:先求平均数;
第二步:再用方差公式计算。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
2.怎样比较两组数据的波动大小呢?
方差越大,数据的波动越____;
方差越小,数据的波动越____.
大
小
3.利用样本方差可以估计总体方差,利用方差
可以分析数据的波动大小。
课本 :第128页,第1题
第3题
六 布置作业
1、夏天,我国西北地区流传民谣“早穿皮袄午穿纱”,而我国南方地区则有“从早到晚不离扇”的说法,下列___统计量 能反映西北地区气温的变化范围;下列_____统计量可以比较两个地区气温波动的大小.
A、众数 B、方差 C、平均数 D、极差 E、中位数
2、甲乙两台机床生产同一种零件,并且每天产量相等, 在6
天中每天生产零件中的次品数依次是:
甲:3、0、0、2、0、1;
乙:1、0、2、1、0、2.
(1)分别求出这两台机床所加工的零件的方差;
(2)说明甲、乙两台机床中哪一台的性能较稳定?
训练案 课堂检测
1、求这四组数据的平均数、方差。
2、对照所填结果,你能从中发现哪些有趣的结论?
数据
平均数
方差
1、2、3、4、5
11、12、13、14、15
10、20、30、40、50
3、6、9、12、15
3
2
13
2
9
18
30
200
若数据x1、x2、…、xn平均数为 ,方差为S2,则
(3)数据ax1±b、ax2±b、…、axn±b
的平均数为 , 方差为a2S2
(1)数据x1±b、x2±b、…、xn±b
的平均数为 , 方差为S2
(2)数据ax1、ax2、…、axn的平均数为 ,
方差为a2S2
已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -.
x+3
y
x-3
y
3x
9y
2x-3
4y
组数据的波动大小呢?
数据的波动程度(1)
1、理解方差概念的产生和形成的过程。会用方差计算公式来比较两组数据的波动大小。
2、培养学生的统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义。
重点:方差产生的必要性和应用方差公式解决实际问题。
难点:理解方差公式,应用方差对数据波动情况的比较、判断。
一、创设情境,引入新知
问题研究:农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如表所示.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
预习案
甲、乙两种甜玉米的平均产量相差不大,由此可以估计出这个地区种植这两种甜玉米,它们的平均产量相差不大.
比较上面两幅图可以看出,甲种甜玉米在各试验田的产量波动较大,乙种甜玉米在各试验田的产量较集中地分布在平均产量附近.从图中看出的结果能否用一个量来刻画呢?
讨论: 1、、如何借助于图分析产量的稳定性?(从形的角度)
2.谁的波动较大?如何用一个量来刻画呢?(从数的角度)
二、理解概念,完善新知
探究案
方差定义
设有n个数据x1,x2,…,xn中,各数据与它们的平均数的差的平方分别是(x1-x)2,(x2-x)2 ,… (xn-x)2 ,那么我们用它们的平均数,即用
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作S2.
由此可知,乙种甜玉米的产量比较稳定,
可以推测,这个地区比较适合种植乙种甜玉米.
讨论:
(1)数据分散(即数据在平均数附近波动较大)时,方差值怎样?
(2)数据集中时,方差值怎样?
(3)方差大小与数据波动性大小有怎样的关系?
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差越大,数据的波动越____;
方差越小,数据的波动越____.
大
小
(4)如何计算一组数据的方差?
第一步:先求平均数;
第二步:再用方差公式计算。
三、解决问题,应用新知
问题1:在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如表所示.
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
解:甲、乙两团演员的平均身高分别是:
由 可知:甲芭蕾舞团女演员的身高更整齐。
方差分别是:
1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的。
(1)6 6 6 6 6 6 6
四 巩固新知
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
巩固新知
2、下列统计量中,能反映一名同学在7—9年级学段
的学习成绩稳定程度的是( )
A、平均数 B、中位数 C、众数 D、方差
3、如果样本方差
那么这个样本的平均数为_____,样本容量为
_____.
D
2
4
巩固新知
4、一组数据:-2,-1,0,x,1的平均数是0,则
X=_____,方差S2=______.
5、为了考察,甲、乙两种小麦的长势,分别从中抽
出20株测得其高度,并求得它们的方差分别为:
则____种小麦的长势比较整齐.
2
2
甲
五 课堂小结
你本节课学到了什么?
1.如何计算一组数据的方差?
第一步:先求平均数;
第二步:再用方差公式计算。
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
2.怎样比较两组数据的波动大小呢?
方差越大,数据的波动越____;
方差越小,数据的波动越____.
大
小
3.利用样本方差可以估计总体方差,利用方差
可以分析数据的波动大小。
课本 :第128页,第1题
第3题
六 布置作业
1、夏天,我国西北地区流传民谣“早穿皮袄午穿纱”,而我国南方地区则有“从早到晚不离扇”的说法,下列___统计量 能反映西北地区气温的变化范围;下列_____统计量可以比较两个地区气温波动的大小.
A、众数 B、方差 C、平均数 D、极差 E、中位数
2、甲乙两台机床生产同一种零件,并且每天产量相等, 在6
天中每天生产零件中的次品数依次是:
甲:3、0、0、2、0、1;
乙:1、0、2、1、0、2.
(1)分别求出这两台机床所加工的零件的方差;
(2)说明甲、乙两台机床中哪一台的性能较稳定?
训练案 课堂检测
1、求这四组数据的平均数、方差。
2、对照所填结果,你能从中发现哪些有趣的结论?
数据
平均数
方差
1、2、3、4、5
11、12、13、14、15
10、20、30、40、50
3、6、9、12、15
3
2
13
2
9
18
30
200
若数据x1、x2、…、xn平均数为 ,方差为S2,则
(3)数据ax1±b、ax2±b、…、axn±b
的平均数为 , 方差为a2S2
(1)数据x1±b、x2±b、…、xn±b
的平均数为 , 方差为S2
(2)数据ax1、ax2、…、axn的平均数为 ,
方差为a2S2
已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -.
x+3
y
x-3
y
3x
9y
2x-3
4y
