人教版数学七年级下册6.2.1《立方根的概念》课件(19张PPT)
文档属性
| 名称 | 人教版数学七年级下册6.2.1《立方根的概念》课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:13:47 | ||
图片预览





文档简介
16的平方根是______
-16的平方根是________
0的平方根是________
没有平方根
0
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
平方根的概念
如果一个数X的平方等于a,即 X2 =a,那么这个数X叫做a的平方根(二次方根)
1、填空:
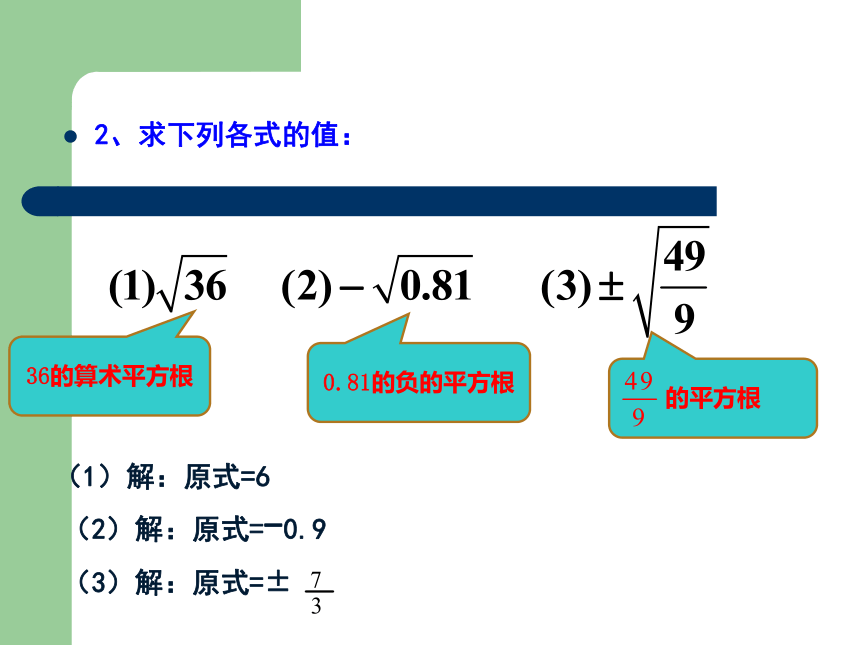
2、求下列各式的值:
36的算术平方根
0.81的负的平方根
的平方根
(1)解:原式=6
(2)解:原式=-0.9
(3)解:原式=±
引入课题:
2、 ( ) =0.125
3、 ( ) =0
4、 ( ) =-8
2
1
-2
0
3
2
-
5 、( )3=
1、 ( ) =8
2
结合学习平方根的过程大家能否尝试得到我们今天要学习的主题是:
立方根
填空:
推出定义:
因为 =8,所以8的立方根是( )
因为( ) =0.125,所以0.125的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根( )
0
2
2
1
2
1
-2
0
-2
3
2
-
3
2
-
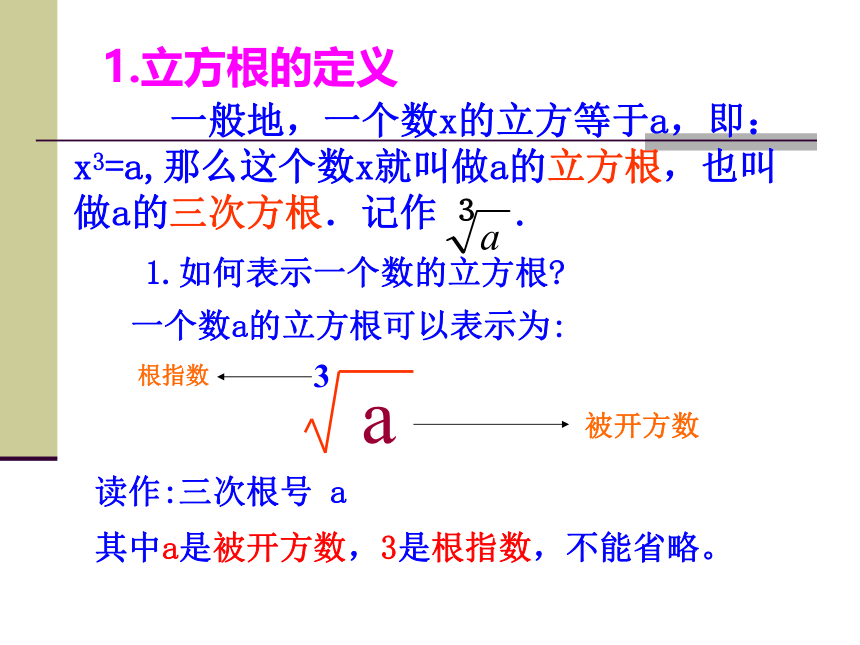
一般地,一个数x的立方等于a,即:x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.记作 .
3
1.立方根的定义
1.如何表示一个数的立方根?
一个数a的立方根可以表示为:
a
3
根指数
被开方数
其中a是被开方数,3是根指数,不能省略。
读作:三次根号 a
学会用数学语言表达:
因为 =8,所以8的立方根是( )
因为( ) =0.125,所以0.125的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根( )
0
2
2
1
2
1
-2
0
-2
3
2
-
3
2
-
3
例:求下列各数的立方根
解:
(1)、(文字语言)
(1)27
∵33=27
∴27的立方根是3
或(数学语言)
3
(2)-64
(3)125
备注:请同学们熟记,1到9的立方值 :
13=1,23=8,33=27,43=64,53=125,
63=216,73=343,83=512,93=729
∵33=27
∴
例:求下列各式的值
(1)
(2)
(3)
解:
(1)
(2)原式= - 5
(3)原式=
3
或 原式= 4
2.立方根的性质
探究1. 根据立方根的意义填空.
因为 =8,所以8的立方根是( )
因为( ) =0.125,所以0.125的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根( )
0
2
2
1
2
1
-2
0
-2
3
2
-
3
2
-
你能看出正数,0,负数的立方根各有什么特点?
正数有立方根吗?如果有,有几个?
负数呢?
零呢?
有一个正的立方根;
有一个负的立方根,
零的立方根是零。
立方根的特征
一个正数有立方根,
一个负数有立方根,
引伸探究2
因为 =
,
=
因为
=
,
=
所以
猜一猜:
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
a
3
-a
3
=
-2
-2
=
-3
-3
互为相反数的数的立方根也互为相反数
读读算式并观察:被开放数与立方根
所以
与
问题:要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:
如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
解:设正方体的棱长为X㎝,则
这就是要求一个数,使它的立方等于27.
因为
所以 X= 正方体的棱长为3㎝
3
3
方程的思想
x3=27
思考:
如果正方体的体积为5cm3,正方体的边长又该是多少?
设正方体的边长为Xcm,则
所以正方体的边长是x=
㎝.
2.求一个数的立方根的运算,叫做开立方
立方
开立方
互逆
到现在我们学了几种运算?
+,-,x,÷,乘方,开方(开平方,开立方)
课堂练习2:
2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)x3-3=24
解:
∴x=7
∴x=3
开立方运算(方程):降次
x3=24+3
x3=27
解:
(1)1的平方根是______;1的立方根为______;1的算术平方根为_________.
(2) - 的立方根为 .
±1
1
1
读读写写
课堂小结
1.立方根的定义,性质,计算.
2.立方根的应用
方程
课后作业:
1、52页,3题
选做,5题
2、完成练习册中本课时的练习.
-16的平方根是________
0的平方根是________
没有平方根
0
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
平方根的概念
如果一个数X的平方等于a,即 X2 =a,那么这个数X叫做a的平方根(二次方根)
1、填空:
2、求下列各式的值:
36的算术平方根
0.81的负的平方根
的平方根
(1)解:原式=6
(2)解:原式=-0.9
(3)解:原式=±
引入课题:
2、 ( ) =0.125
3、 ( ) =0
4、 ( ) =-8
2
1
-2
0
3
2
-
5 、( )3=
1、 ( ) =8
2
结合学习平方根的过程大家能否尝试得到我们今天要学习的主题是:
立方根
填空:
推出定义:
因为 =8,所以8的立方根是( )
因为( ) =0.125,所以0.125的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根( )
0
2
2
1
2
1
-2
0
-2
3
2
-
3
2
-
一般地,一个数x的立方等于a,即:x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.记作 .
3
1.立方根的定义
1.如何表示一个数的立方根?
一个数a的立方根可以表示为:
a
3
根指数
被开方数
其中a是被开方数,3是根指数,不能省略。
读作:三次根号 a
学会用数学语言表达:
因为 =8,所以8的立方根是( )
因为( ) =0.125,所以0.125的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根( )
0
2
2
1
2
1
-2
0
-2
3
2
-
3
2
-
3
例:求下列各数的立方根
解:
(1)、(文字语言)
(1)27
∵33=27
∴27的立方根是3
或(数学语言)
3
(2)-64
(3)125
备注:请同学们熟记,1到9的立方值 :
13=1,23=8,33=27,43=64,53=125,
63=216,73=343,83=512,93=729
∵33=27
∴
例:求下列各式的值
(1)
(2)
(3)
解:
(1)
(2)原式= - 5
(3)原式=
3
或 原式= 4
2.立方根的性质
探究1. 根据立方根的意义填空.
因为 =8,所以8的立方根是( )
因为( ) =0.125,所以0.125的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根( )
0
2
2
1
2
1
-2
0
-2
3
2
-
3
2
-
你能看出正数,0,负数的立方根各有什么特点?
正数有立方根吗?如果有,有几个?
负数呢?
零呢?
有一个正的立方根;
有一个负的立方根,
零的立方根是零。
立方根的特征
一个正数有立方根,
一个负数有立方根,
引伸探究2
因为 =
,
=
因为
=
,
=
所以
猜一猜:
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
a
3
-a
3
=
-2
-2
=
-3
-3
互为相反数的数的立方根也互为相反数
读读算式并观察:被开放数与立方根
所以
与
问题:要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:
如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
解:设正方体的棱长为X㎝,则
这就是要求一个数,使它的立方等于27.
因为
所以 X= 正方体的棱长为3㎝
3
3
方程的思想
x3=27
思考:
如果正方体的体积为5cm3,正方体的边长又该是多少?
设正方体的边长为Xcm,则
所以正方体的边长是x=
㎝.
2.求一个数的立方根的运算,叫做开立方
立方
开立方
互逆
到现在我们学了几种运算?
+,-,x,÷,乘方,开方(开平方,开立方)
课堂练习2:
2.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)x3-3=24
解:
∴x=7
∴x=3
开立方运算(方程):降次
x3=24+3
x3=27
解:
(1)1的平方根是______;1的立方根为______;1的算术平方根为_________.
(2) - 的立方根为 .
±1
1
1
读读写写
课堂小结
1.立方根的定义,性质,计算.
2.立方根的应用
方程
课后作业:
1、52页,3题
选做,5题
2、完成练习册中本课时的练习.
