人教版数学七年级下册8.2解二元一次方程组课件(共24张PPT)
文档属性
| 名称 | 人教版数学七年级下册8.2解二元一次方程组课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 431.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:09:31 | ||
图片预览







文档简介
(共21张PPT)
8.2.4 用适当方法解二元一次方程组
梳理旧知
解二元一次方程组的基本思想是什么?
二元一次方程
一元一次方程
消元
转化
消元的方法有哪些?
代入消元法; 加减消元法
运动会闭幕式学校领导发言
各位领导、老师,全体同学们:
xx中XX年春季田径运动会,在学校的正确领导下,经过运动会组委会的精心筹备,在广大师生员工的精诚配合下,圆满地完成了各项比赛任务,取得了预期的效果,现在就要闭幕了。
本届校运会,充分展示了“阳光体育”的主题。在短短的3天时间里,比赛进程井然有序,紧凑而热烈,效率是很高的,成绩是喜人的。本次运动会一共有1389名运动员参加了30个比赛项目的紧张角逐,有12人次刷新学校田径运动会的纪录,有66人次分别获得第一、二、三名,涌现了7个优胜班集体,2个体育道德风尚先进班级,xx同学获得校长提名体育精神文明奖。在此,让我们以热烈的掌声对他们表示最诚挚的祝贺!
全体工作人员的恪尽职守,运动员的杰出表现和骄人的比赛成绩,让我们看到了成功教育理念下,全体师生的成功表现,也让我们看到了我校体育事业的希望和推动学校工作全面发展的美好的未来。今天,我校XX年春季田径运动会的所有活动已经划上了一个完满的句号。在本届校运会中,全体裁判员始终严格要求自己,认真负责,坚持标准,以身作则,以公平、公正、公开的工作作风,保证本届校运会的圆满完成。广大教师和学生在活动
提出问题
选择哪种方法解方程更简便?为什么?
(1)
(2)
(3)
(4)
(5)
方法总结
1、代入消元法:
方程组中有一个未知数的系数
为1(或-1)。
如:
提出问题
选择哪种方法解方程更简便?为什么?
(3)
(4)
方法总结
2、加减消元法:
(1)方程组中有某个未知数的系数相同或互为相反数;
(2)同一个未知数的系数成倍数关系;
如
提出问题
选择哪种方法解方程更简便?为什么?
(5)
方法总结
(3)求同一系数的最小公倍数。
特别强调:对于较复杂的二元一次方程组应先化简(去分母、去括号、合并同类项等)
如
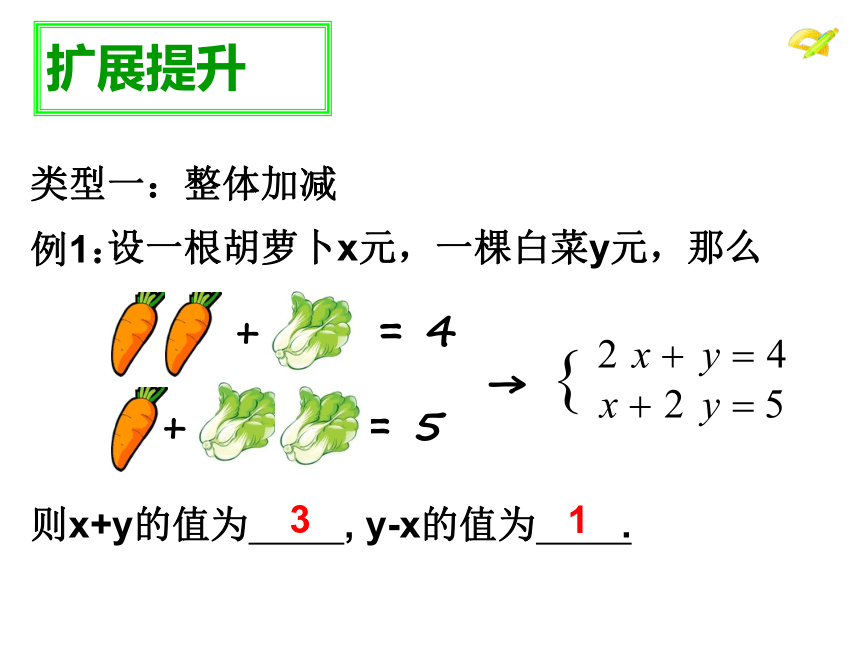
类型一:整体加减
例1:
则x+y的值为 , y-x的值为 .
3
扩展提升
1
+
=
4
+
=
5
→
设一根胡萝卜x元,一棵白菜y元,那么
变式1:若 ,求
的值
分析:上述方程中两个方程可作整体相加,整体相减而解出。
解:由方程①-②得: -x+y=-3,即 x-y=3; 由方程①+②得: 4009x+4009y=4009,即 x+y=1; ∴
变式1:若 ,求
的值
扩展提升
变式2:已知方程 的解满足x+y=1,求m的值。
分析:两方程相加得x+y=m,很明显得到m=1.
扩展提升
例2:解方程组
分析:方程①及②中均含有 。可用整体思想解。由①得 代入②而求出y。
类型二:整体代入
变式:解方程组
解:把 ②代入 ①,得 x+2 2=4,解得 x=0
把x=0代入②,解得y=1
所以方程组的解是
扩展提升
例3:解方程组
分析:本题含有相同的式子,可用换元法求解。
换元思想是重要的数学思想!
类型三:整体“换元”
解:设 , ,
原方程化为
解得
例3:解方程组
原方程组变为
即
解得
扩展提升
变式:解方程组
分析:若先去括号,去分母等变形显得十分烦琐,观察上述方程中特点将( )、( )作整体且( )系数相同,可用整体换元。
扩展提升
变式:解方程组
解得
归纳总结
回顾本节课的学习过程,回答以下问题:
(1)如何选择代入法和加减法使运算更简便?
(2)应用整体思想巧妙解决二元一次方程组的核心是什么?
课后作业
1、
已知方程组 的解x,y满足方程5x-y=3,求k的值.
2、解方程组
分析:本题未知数的系数差是定值,可以凭此作差将方程组变形.
悟性的高低取决于“有心”,其实,人与人的差别就在于你是否去思考,去发现,去总结.同学们,相信自己,你们是最棒的!
8.2.4 用适当方法解二元一次方程组
梳理旧知
解二元一次方程组的基本思想是什么?
二元一次方程
一元一次方程
消元
转化
消元的方法有哪些?
代入消元法; 加减消元法
运动会闭幕式学校领导发言
各位领导、老师,全体同学们:
xx中XX年春季田径运动会,在学校的正确领导下,经过运动会组委会的精心筹备,在广大师生员工的精诚配合下,圆满地完成了各项比赛任务,取得了预期的效果,现在就要闭幕了。
本届校运会,充分展示了“阳光体育”的主题。在短短的3天时间里,比赛进程井然有序,紧凑而热烈,效率是很高的,成绩是喜人的。本次运动会一共有1389名运动员参加了30个比赛项目的紧张角逐,有12人次刷新学校田径运动会的纪录,有66人次分别获得第一、二、三名,涌现了7个优胜班集体,2个体育道德风尚先进班级,xx同学获得校长提名体育精神文明奖。在此,让我们以热烈的掌声对他们表示最诚挚的祝贺!
全体工作人员的恪尽职守,运动员的杰出表现和骄人的比赛成绩,让我们看到了成功教育理念下,全体师生的成功表现,也让我们看到了我校体育事业的希望和推动学校工作全面发展的美好的未来。今天,我校XX年春季田径运动会的所有活动已经划上了一个完满的句号。在本届校运会中,全体裁判员始终严格要求自己,认真负责,坚持标准,以身作则,以公平、公正、公开的工作作风,保证本届校运会的圆满完成。广大教师和学生在活动
提出问题
选择哪种方法解方程更简便?为什么?
(1)
(2)
(3)
(4)
(5)
方法总结
1、代入消元法:
方程组中有一个未知数的系数
为1(或-1)。
如:
提出问题
选择哪种方法解方程更简便?为什么?
(3)
(4)
方法总结
2、加减消元法:
(1)方程组中有某个未知数的系数相同或互为相反数;
(2)同一个未知数的系数成倍数关系;
如
提出问题
选择哪种方法解方程更简便?为什么?
(5)
方法总结
(3)求同一系数的最小公倍数。
特别强调:对于较复杂的二元一次方程组应先化简(去分母、去括号、合并同类项等)
如
类型一:整体加减
例1:
则x+y的值为 , y-x的值为 .
3
扩展提升
1
+
=
4
+
=
5
→
设一根胡萝卜x元,一棵白菜y元,那么
变式1:若 ,求
的值
分析:上述方程中两个方程可作整体相加,整体相减而解出。
解:由方程①-②得: -x+y=-3,即 x-y=3; 由方程①+②得: 4009x+4009y=4009,即 x+y=1; ∴
变式1:若 ,求
的值
扩展提升
变式2:已知方程 的解满足x+y=1,求m的值。
分析:两方程相加得x+y=m,很明显得到m=1.
扩展提升
例2:解方程组
分析:方程①及②中均含有 。可用整体思想解。由①得 代入②而求出y。
类型二:整体代入
变式:解方程组
解:把 ②代入 ①,得 x+2 2=4,解得 x=0
把x=0代入②,解得y=1
所以方程组的解是
扩展提升
例3:解方程组
分析:本题含有相同的式子,可用换元法求解。
换元思想是重要的数学思想!
类型三:整体“换元”
解:设 , ,
原方程化为
解得
例3:解方程组
原方程组变为
即
解得
扩展提升
变式:解方程组
分析:若先去括号,去分母等变形显得十分烦琐,观察上述方程中特点将( )、( )作整体且( )系数相同,可用整体换元。
扩展提升
变式:解方程组
解得
归纳总结
回顾本节课的学习过程,回答以下问题:
(1)如何选择代入法和加减法使运算更简便?
(2)应用整体思想巧妙解决二元一次方程组的核心是什么?
课后作业
1、
已知方程组 的解x,y满足方程5x-y=3,求k的值.
2、解方程组
分析:本题未知数的系数差是定值,可以凭此作差将方程组变形.
悟性的高低取决于“有心”,其实,人与人的差别就在于你是否去思考,去发现,去总结.同学们,相信自己,你们是最棒的!
