沪教版(上海)数学八年级第二学期-22.4 梯形复习 课件(27张)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.4 梯形复习 课件(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:09:27 | ||
图片预览



文档简介
(共27张PPT)
梯形复习
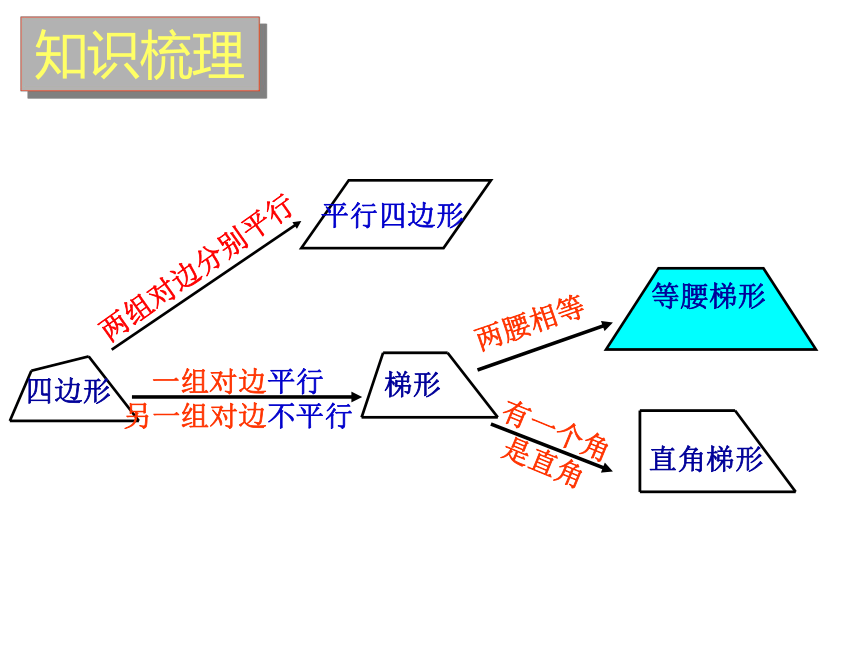
梯形
等腰梯形
直角梯形
两腰相等
有一个角
是直角
四边形
一组对边平行
另一组对边不平行
知识梳理
两组对边分别平行
平行四边形
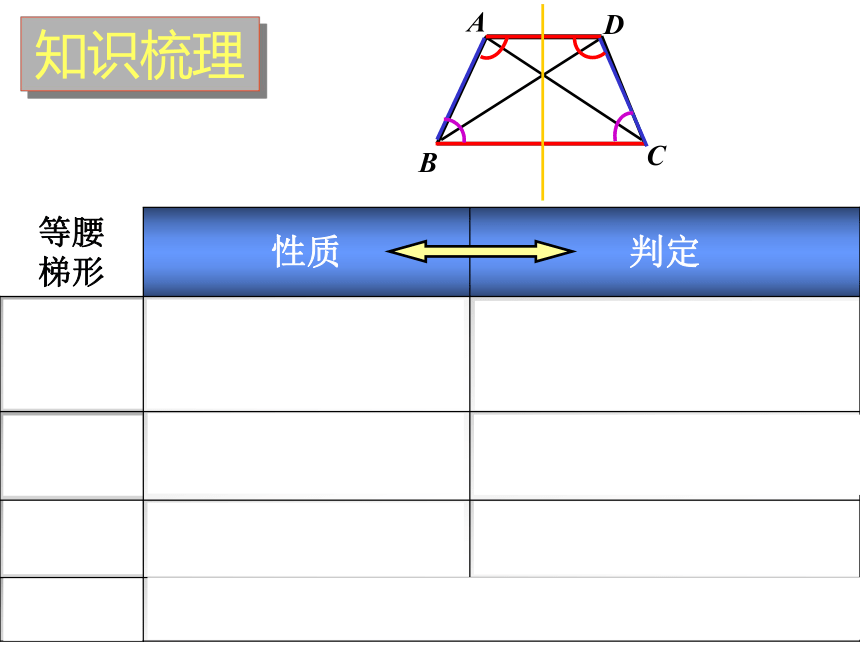
等腰
梯形
性质
判定
边
两底平行,两腰相等
两腰相等的梯形是等腰梯形
角
同一底上的两个角相等
同一底上的两个角相等的梯形是等腰梯形
对角线
两条对角线相等
两条对角线相等的梯形是等腰梯形
对称性
等腰梯形是轴对称图形,对称轴是一底的中垂线
知识梳理
C
B
D
A
1.一组对边相等,另一组对边平行的四边形是等腰梯形.
(
)
2.有两个角相等的梯形是等腰梯形.
(
)
3.一组对边平行但不相等的四边形是梯形.
(
)
4.两组对角分别互补的四边形一定是等腰梯形.
(
)
×
×
√
×
典型习题
例1
判断下列说法是否正确:
C
B
D
A
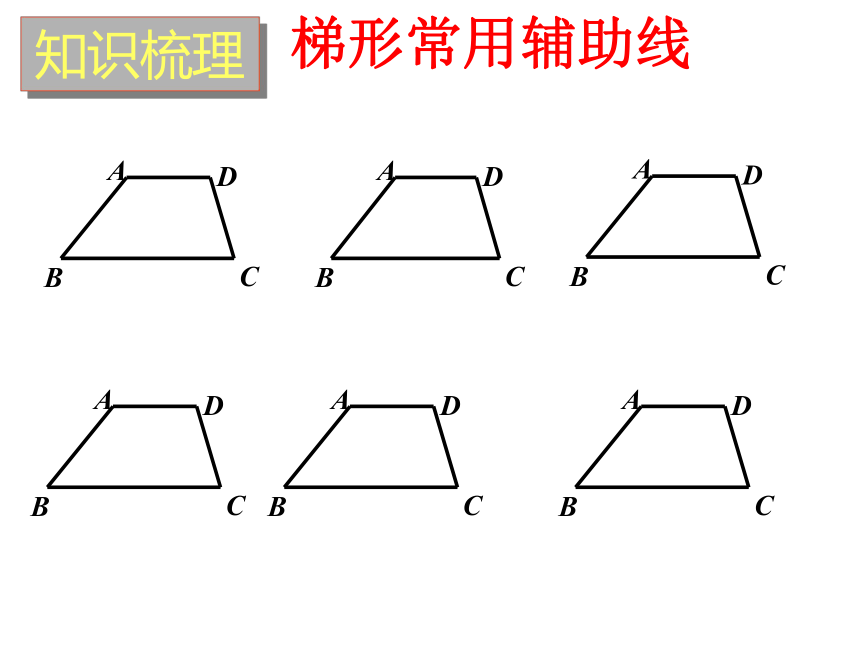
梯形常用辅助线
知识梳理
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
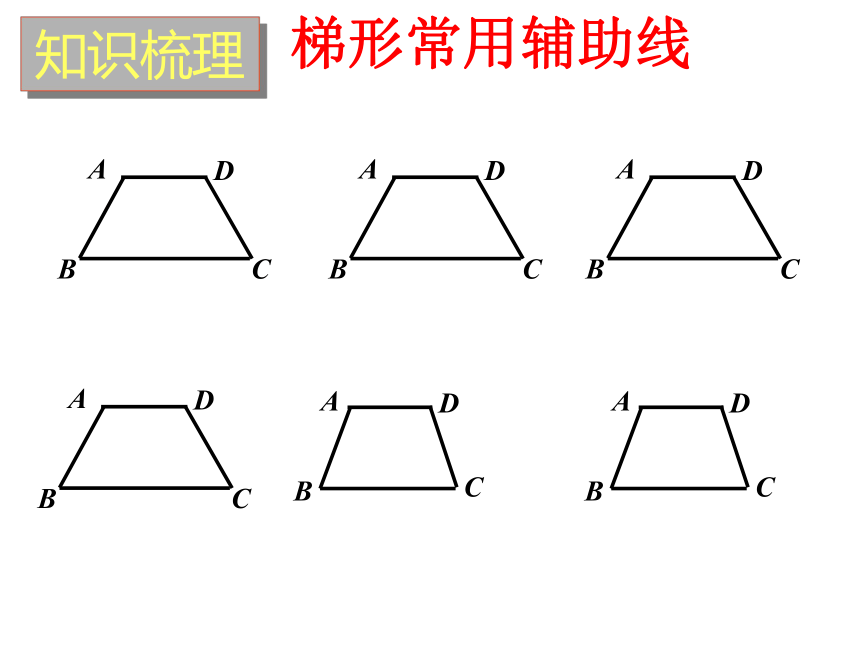
梯形常用辅助线
知识梳理
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
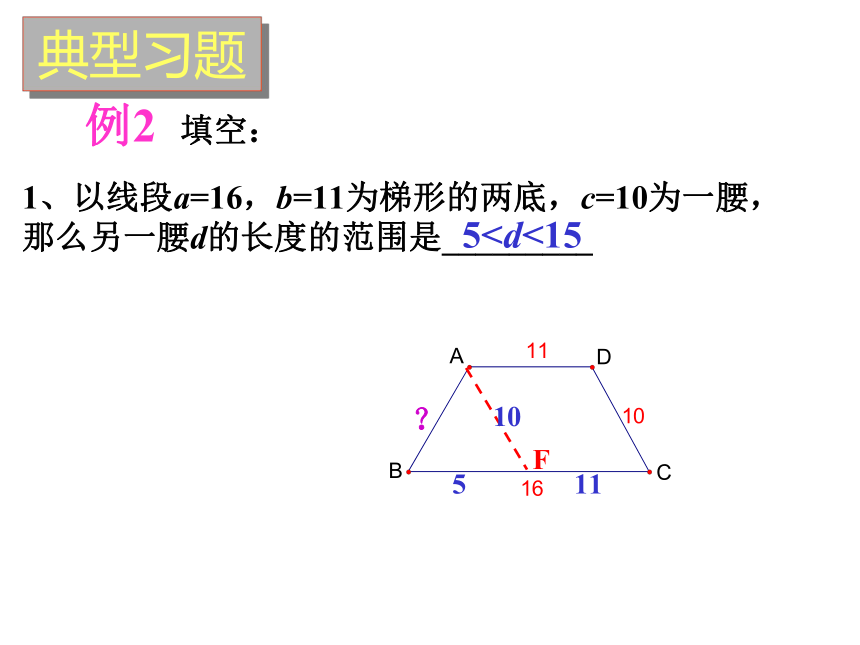
1、以线段a=16,b=11为梯形的两底,c=10为一腰,那么另一腰d的长度的范围是_________
510
11
5
?
典型习题
例2
填空:
F
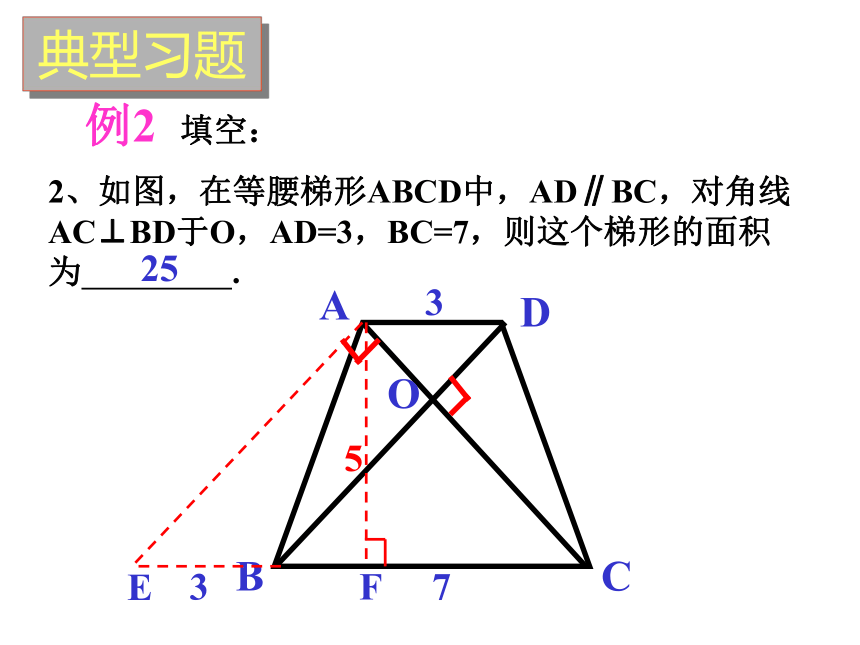
2、如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于O,AD=3,BC=7,则这个梯形的面积为
.
A
B
C
D
O
典型习题
例2
填空:
3
7
3
E
F
5
25
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,
BC=21cm,点P从点A开始沿AD边向点D以1cm/s的速度移动,点Q从点C开始沿CB向点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,设移动的时间为t秒,求t为何值时梯形PQCD是等腰梯形?
典型习题
例3
18
21
t
18-t
2t
3
3
E
F
A
B
C
D
P
Q
解:由题意得,AP=t(cm),CQ=2t(cm),则
PD=18-t(cm),
过点D作DE⊥BC于点E,
∴四边形ABED是矩形,
又∵四边形PQCD是等腰梯形,
易证得△PQF∽△DCE,
∴QF=CE=3cm,
∴EF=PD=18-t(cm),
∴QF+EF+EC=QC
即3+(18-t)+3=2t,
解得,t=8.
答:当t为8s时梯形PQCD是等腰梯形.
∵AD∥BC,∠B=90°,
∴∠A=90°
∵AD=18cm,
BC=21cm
,
∴EC=3cm
过点P作PE⊥BC于点F,
通过这节课的学习,你有什么收获?
小结
梯形
等腰梯形
直角梯形
两腰相等
有一个角
是直角
四边形
一组对边平行
另一组对边不平行
两组对边分别平行
平行四边形
四边形与梯形的关系及梯形的分类
梯形问题
转化
小结
三角形或平行四边形
添加辅助线
梯形中常作的辅助线
.
.
小结
谢谢!
1.延长两腰交于一点
A
B
D
C
E
2.平移一腰
A
B
D
C
E
梯形常用辅助线
CE等于上、下底的差
作用:使梯形问题转化为三角形问题,
若是等腰梯形则得到等腰三角形.
作用:使梯形问题转化为平行四边形
及三角形问题.
小结
3.作高
A
B
D
C
E
F
梯形常用辅助线
4.平移一条对角线
A
B
C
D
E
BE等于上、下底的和
作用:使梯形问题转化为直角三角形
及矩形问题.
作用:得到平行四边形ACED,可知CE=AD.
S△DEB=
S
梯形ABCD
小结
5.
当有一腰中点时,联结一个顶点与一腰中点并延长与另一个底的延长线相交.
C
B
F
E
D
A
C
B
F
E
D
A
G
6.
当有一腰中点时,过中点作另一腰的平行线.
梯形常用辅助线
作用:可得△ADE≌△FCE,
BF等于上、下底的和.
BF等于上、下底的和
作用:可得到平行四边形和全等三角形.
S△ABF=
S
梯形ABCD
S
ABGF=
S
梯形ABCD
小结
A
B
C
D
E
1、如图,在梯形ABCD中,
AD∥BC,AB=CD,
求证:∠B=
∠C.
课后练习
2、如图,在梯形ABCD中,AD∥BC,∠B与∠C互余,AD=5,BC=13,
∠C=60°则该梯形的面积是多少?
B
A
C
D
E
F
课后练习
3、在等腰梯形ABCD中,AB∥DC,∠D=60
°,
AB=2,AD=4,求:梯形ABCD
的周长。
A
B
C
D
E
课后练习
4、如图,在梯形ABCD中,AD∥BC,AB=CD,
且AC⊥BD,AF是梯形的高,梯形面积为49c㎡,求AF的长.
A
B
F
C
D
O
E
课后练习
5、在梯形ABCD中,AD∥BC,
AC
⊥
BD,且AC=5cm,BD=12cm,求梯形两底之和.
O
D
C
B
A
E
课后练习
6、已知梯形ABCD中,AD∥BC,AD=6cm,BC=12cm,且AC=BD,AC⊥BD.
求:S梯形ABCD
A
B
C
D
H
E
课后练习
7、
在梯形ABCD中,AD∥BC,
AB=DC=AD,DC⊥BD,
若周长为20,
求梯形各内角及各边长。
A
B
C
D
课后练习
8、已知:如图,直角梯形ABCD中,
AD∥BC,
∠A=90。,∠D=150。
CD=8cm,
求AB的长。
A
B
C
D
E
课后练习
1、如图,在等腰梯形ABCD中,AB∥CD,AD=BC,∠A=600,AB=9,CD=5,BC的长是(
)
A.
3
B.
4
C.5
D.6
B
A
D
C
2、如图,在梯形ABCD中,AD∥BC,AB=DC,∠C=60°,BD平分∠ABC,如果这个梯形的周长为30,则AB的长是(
)
A.4
B.5
C.6
D.7
3、在梯形ABCD中,AD∥BC,M是CD的中点,AF
⊥
BC于F,
∠B=45°
AF=3,EF=5则梯形ABCD的面积为()
A、24
B、12
C、6
D、16
A
D
B
C
M
E
F
梯形复习
梯形
等腰梯形
直角梯形
两腰相等
有一个角
是直角
四边形
一组对边平行
另一组对边不平行
知识梳理
两组对边分别平行
平行四边形
等腰
梯形
性质
判定
边
两底平行,两腰相等
两腰相等的梯形是等腰梯形
角
同一底上的两个角相等
同一底上的两个角相等的梯形是等腰梯形
对角线
两条对角线相等
两条对角线相等的梯形是等腰梯形
对称性
等腰梯形是轴对称图形,对称轴是一底的中垂线
知识梳理
C
B
D
A
1.一组对边相等,另一组对边平行的四边形是等腰梯形.
(
)
2.有两个角相等的梯形是等腰梯形.
(
)
3.一组对边平行但不相等的四边形是梯形.
(
)
4.两组对角分别互补的四边形一定是等腰梯形.
(
)
×
×
√
×
典型习题
例1
判断下列说法是否正确:
C
B
D
A
梯形常用辅助线
知识梳理
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
梯形常用辅助线
知识梳理
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
D
A
1、以线段a=16,b=11为梯形的两底,c=10为一腰,那么另一腰d的长度的范围是_________
5
11
5
?
典型习题
例2
填空:
F
2、如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于O,AD=3,BC=7,则这个梯形的面积为
.
A
B
C
D
O
典型习题
例2
填空:
3
7
3
E
F
5
25
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,
BC=21cm,点P从点A开始沿AD边向点D以1cm/s的速度移动,点Q从点C开始沿CB向点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,设移动的时间为t秒,求t为何值时梯形PQCD是等腰梯形?
典型习题
例3
18
21
t
18-t
2t
3
3
E
F
A
B
C
D
P
Q
解:由题意得,AP=t(cm),CQ=2t(cm),则
PD=18-t(cm),
过点D作DE⊥BC于点E,
∴四边形ABED是矩形,
又∵四边形PQCD是等腰梯形,
易证得△PQF∽△DCE,
∴QF=CE=3cm,
∴EF=PD=18-t(cm),
∴QF+EF+EC=QC
即3+(18-t)+3=2t,
解得,t=8.
答:当t为8s时梯形PQCD是等腰梯形.
∵AD∥BC,∠B=90°,
∴∠A=90°
∵AD=18cm,
BC=21cm
,
∴EC=3cm
过点P作PE⊥BC于点F,
通过这节课的学习,你有什么收获?
小结
梯形
等腰梯形
直角梯形
两腰相等
有一个角
是直角
四边形
一组对边平行
另一组对边不平行
两组对边分别平行
平行四边形
四边形与梯形的关系及梯形的分类
梯形问题
转化
小结
三角形或平行四边形
添加辅助线
梯形中常作的辅助线
.
.
小结
谢谢!
1.延长两腰交于一点
A
B
D
C
E
2.平移一腰
A
B
D
C
E
梯形常用辅助线
CE等于上、下底的差
作用:使梯形问题转化为三角形问题,
若是等腰梯形则得到等腰三角形.
作用:使梯形问题转化为平行四边形
及三角形问题.
小结
3.作高
A
B
D
C
E
F
梯形常用辅助线
4.平移一条对角线
A
B
C
D
E
BE等于上、下底的和
作用:使梯形问题转化为直角三角形
及矩形问题.
作用:得到平行四边形ACED,可知CE=AD.
S△DEB=
S
梯形ABCD
小结
5.
当有一腰中点时,联结一个顶点与一腰中点并延长与另一个底的延长线相交.
C
B
F
E
D
A
C
B
F
E
D
A
G
6.
当有一腰中点时,过中点作另一腰的平行线.
梯形常用辅助线
作用:可得△ADE≌△FCE,
BF等于上、下底的和.
BF等于上、下底的和
作用:可得到平行四边形和全等三角形.
S△ABF=
S
梯形ABCD
S
ABGF=
S
梯形ABCD
小结
A
B
C
D
E
1、如图,在梯形ABCD中,
AD∥BC,AB=CD,
求证:∠B=
∠C.
课后练习
2、如图,在梯形ABCD中,AD∥BC,∠B与∠C互余,AD=5,BC=13,
∠C=60°则该梯形的面积是多少?
B
A
C
D
E
F
课后练习
3、在等腰梯形ABCD中,AB∥DC,∠D=60
°,
AB=2,AD=4,求:梯形ABCD
的周长。
A
B
C
D
E
课后练习
4、如图,在梯形ABCD中,AD∥BC,AB=CD,
且AC⊥BD,AF是梯形的高,梯形面积为49c㎡,求AF的长.
A
B
F
C
D
O
E
课后练习
5、在梯形ABCD中,AD∥BC,
AC
⊥
BD,且AC=5cm,BD=12cm,求梯形两底之和.
O
D
C
B
A
E
课后练习
6、已知梯形ABCD中,AD∥BC,AD=6cm,BC=12cm,且AC=BD,AC⊥BD.
求:S梯形ABCD
A
B
C
D
H
E
课后练习
7、
在梯形ABCD中,AD∥BC,
AB=DC=AD,DC⊥BD,
若周长为20,
求梯形各内角及各边长。
A
B
C
D
课后练习
8、已知:如图,直角梯形ABCD中,
AD∥BC,
∠A=90。,∠D=150。
CD=8cm,
求AB的长。
A
B
C
D
E
课后练习
1、如图,在等腰梯形ABCD中,AB∥CD,AD=BC,∠A=600,AB=9,CD=5,BC的长是(
)
A.
3
B.
4
C.5
D.6
B
A
D
C
2、如图,在梯形ABCD中,AD∥BC,AB=DC,∠C=60°,BD平分∠ABC,如果这个梯形的周长为30,则AB的长是(
)
A.4
B.5
C.6
D.7
3、在梯形ABCD中,AD∥BC,M是CD的中点,AF
⊥
BC于F,
∠B=45°
AF=3,EF=5则梯形ABCD的面积为()
A、24
B、12
C、6
D、16
A
D
B
C
M
E
F
