沪科版八年级数学上册第14章全等三角形单元同步训练题(Word版 含简单答案)
文档属性
| 名称 | 沪科版八年级数学上册第14章全等三角形单元同步训练题(Word版 含简单答案) | 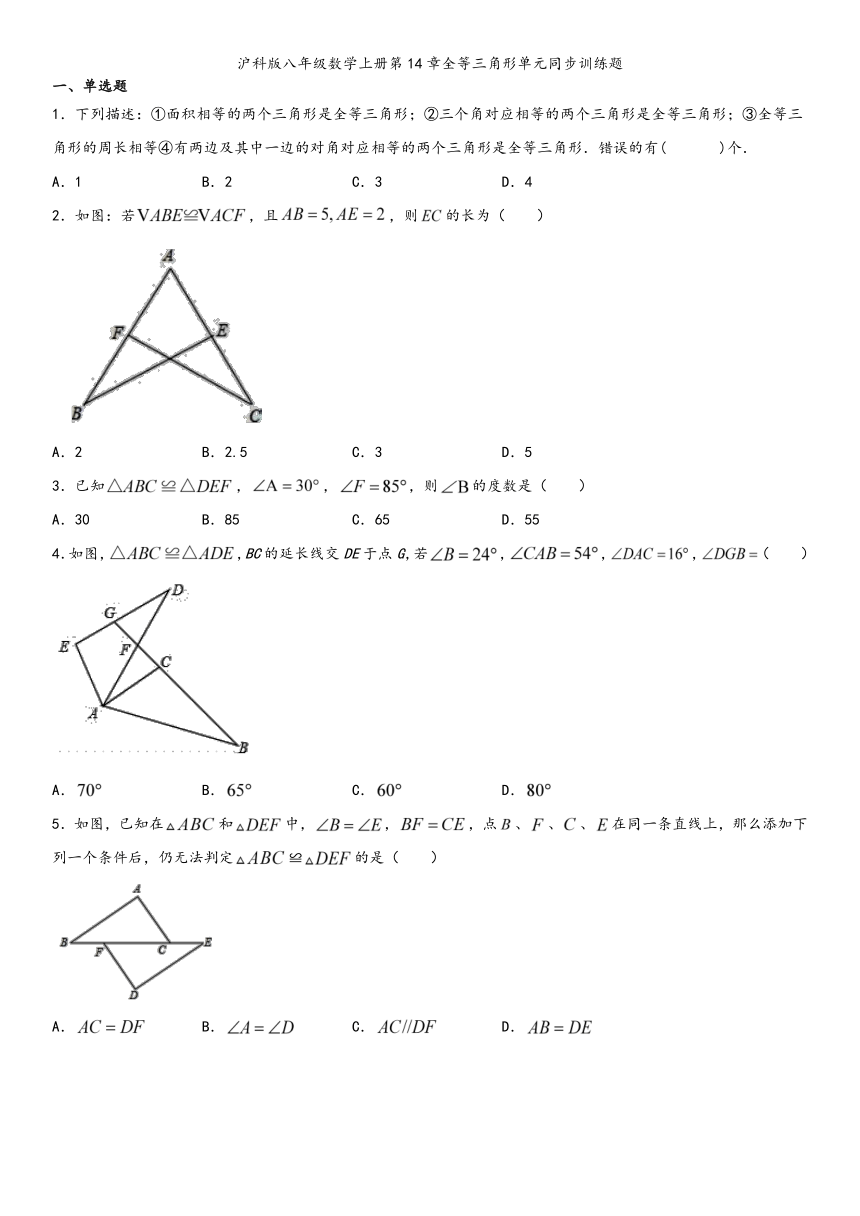 | |
| 格式 | zip | ||
| 文件大小 | 220.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:27:10 | ||
图片预览

文档简介
沪科版八年级数学上册第14章全等三角形单元同步训练题
一、单选题
1.下列描述:①面积相等的两个三角形是全等三角形;②三个角对应相等的两个三角形是全等三角形;③全等三角形的周长相等④有两边及其中一边的对角对应相等的两个三角形是全等三角形.错误的有(
)个.
A.1
B.2
C.3
D.4
2.如图:若,且,则的长为(
)
A.2
B.2.5
C.3
D.5
3.已知,,,则的度数是(
)
A.30
B.85
C.65
D.55
4.如图,,BC的延长线交DE于点G,若,,,(
)
A.
B.
C.
D.
5.如图,已知在和中,,,点、、、在同一条直线上,那么添加下列一个条件后,仍无法判定≌的是(
)
A.
B.
C.
D.
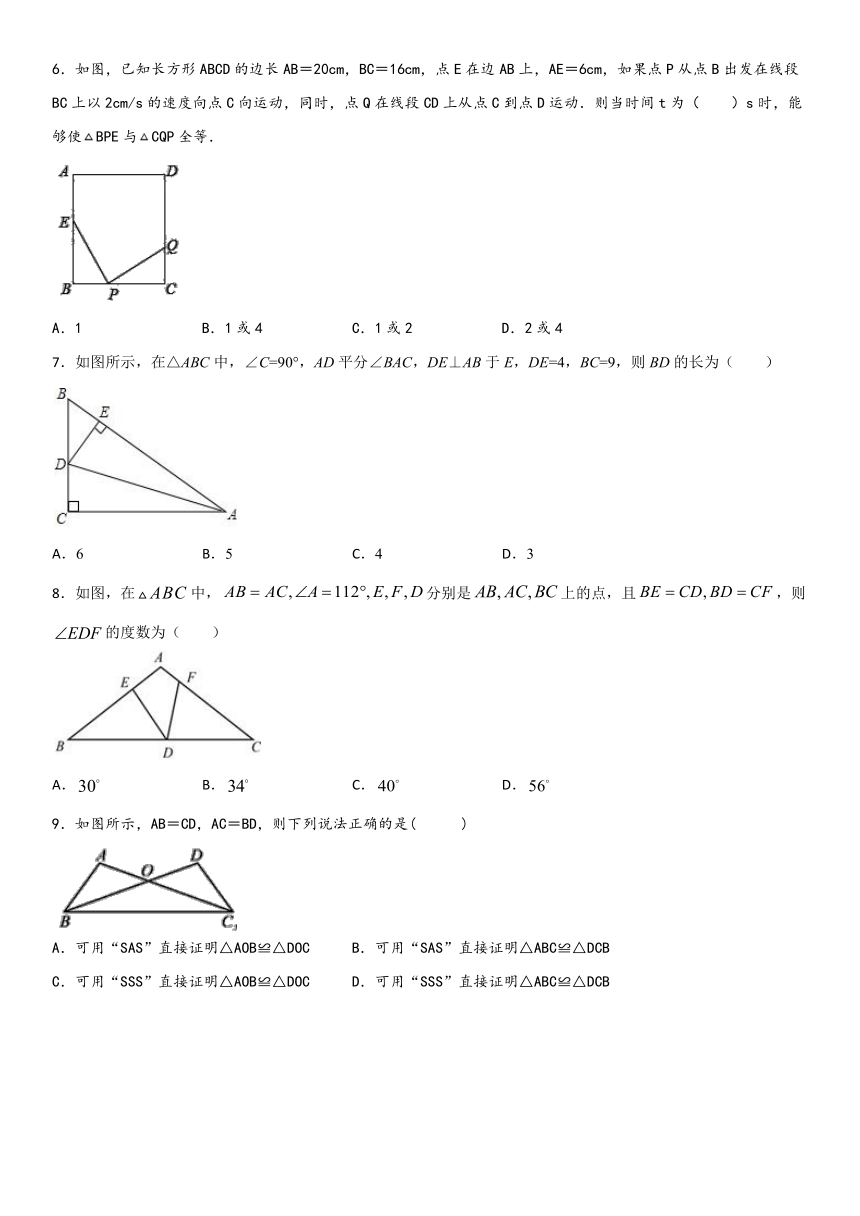
6.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使BPE与CQP全等.
A.1
B.1或4
C.1或2
D.2或4
7.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6
B.5
C.4
D.3
8.如图,在中,分别是上的点,且,则的度数为(
)
A.
B.
C.
D.
9.如图所示,AB=CD,AC=BD,则下列说法正确的是(
)
A.可用“SAS”直接证明△AOB≌△DOC
B.可用“SAS”直接证明△ABC≌△DCB
C.可用“SSS”直接证明△AOB≌△DOC
D.可用“SSS”直接证明△ABC≌△DCB
10.如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是(
)
A.PD=DQ
B.DE=AC
C.AE=CQ
D.PQ⊥AB
二、填空题
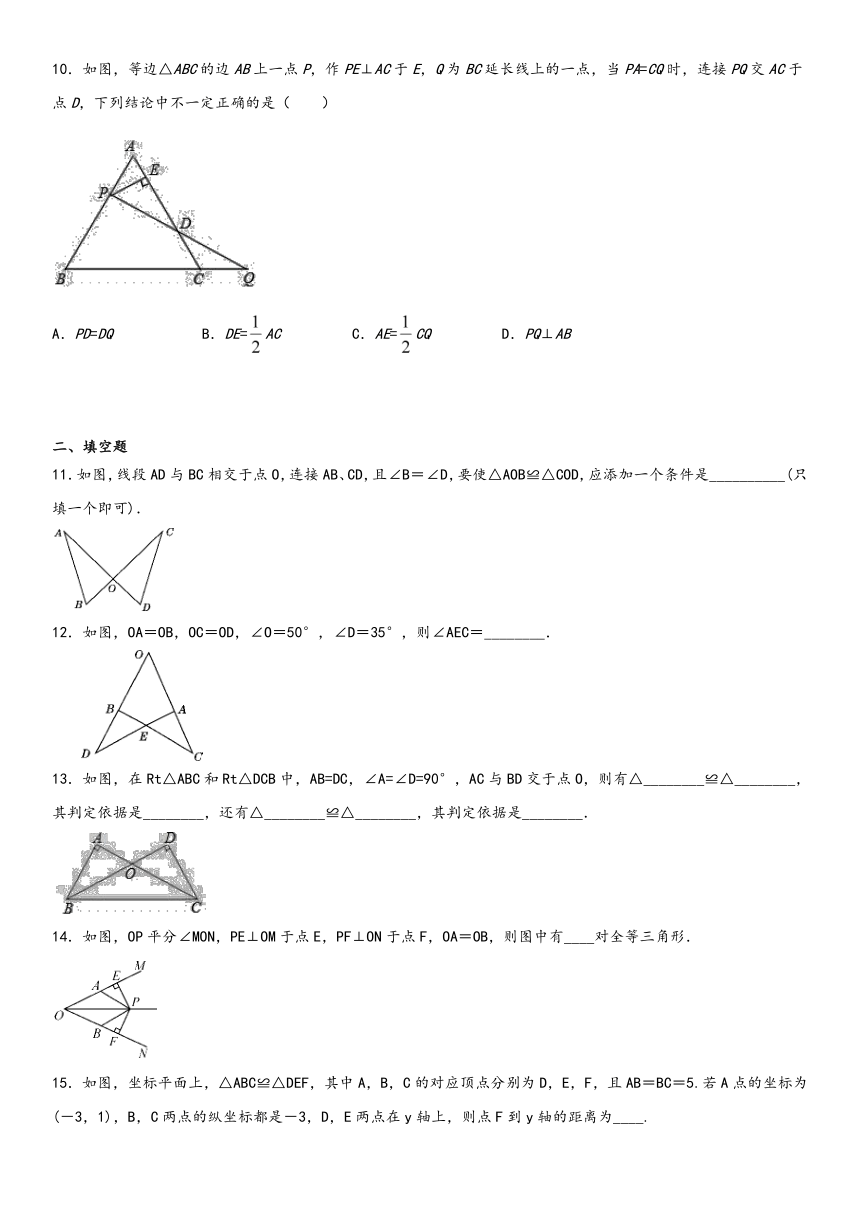
11.如图,线段AD与BC相交于点O,连接AB、CD,且∠B=∠D,要使△AOB≌△COD,应添加一个条件是__________(只填一个即可).
12.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC=________.
13.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.
14.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中有____对全等三角形.
15.如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为____.
三、解答题
16.如图:
是的高,为上一点,交于,且有.
求证:.
17.如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.
18.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.
19.如图,G
为
BC
的中点,且
DG⊥BC,DE⊥AB
于
E,DF⊥AC
于
F,
BE=CF.
(1)求证:AD
是∠BAC
的平分线;
(2)如果
AB=8,AC=6,求
AE
的长.
20.如图,中,,D,E,F分别为AB,BC,CA上的点,且,.
(1)求证:≌;
(2)若,求的度数.
21.如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.
22.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,
CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
试卷第1页,总3页
参考答案
1.C2.C3.C4.A5.A6.B7.B8.B9.D10.D
11.OB=OD(或AO=CO或AB=CD)
12.60°
13.ABC,
DCB,
HL,
AOB,
DOC,
AAS.
14.3
15.4
18.(2).
19.(2)7.
20.(2)55°.
21.(1)四边形ACGD为平行四边形
22.(2)成立(3)△DEF为等边三角形
一、单选题
1.下列描述:①面积相等的两个三角形是全等三角形;②三个角对应相等的两个三角形是全等三角形;③全等三角形的周长相等④有两边及其中一边的对角对应相等的两个三角形是全等三角形.错误的有(
)个.
A.1
B.2
C.3
D.4
2.如图:若,且,则的长为(
)
A.2
B.2.5
C.3
D.5
3.已知,,,则的度数是(
)
A.30
B.85
C.65
D.55
4.如图,,BC的延长线交DE于点G,若,,,(
)
A.
B.
C.
D.
5.如图,已知在和中,,,点、、、在同一条直线上,那么添加下列一个条件后,仍无法判定≌的是(
)
A.
B.
C.
D.
6.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使BPE与CQP全等.
A.1
B.1或4
C.1或2
D.2或4
7.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6
B.5
C.4
D.3
8.如图,在中,分别是上的点,且,则的度数为(
)
A.
B.
C.
D.
9.如图所示,AB=CD,AC=BD,则下列说法正确的是(
)
A.可用“SAS”直接证明△AOB≌△DOC
B.可用“SAS”直接证明△ABC≌△DCB
C.可用“SSS”直接证明△AOB≌△DOC
D.可用“SSS”直接证明△ABC≌△DCB
10.如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是(
)
A.PD=DQ
B.DE=AC
C.AE=CQ
D.PQ⊥AB
二、填空题
11.如图,线段AD与BC相交于点O,连接AB、CD,且∠B=∠D,要使△AOB≌△COD,应添加一个条件是__________(只填一个即可).
12.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC=________.
13.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.
14.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中有____对全等三角形.
15.如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为____.
三、解答题
16.如图:
是的高,为上一点,交于,且有.
求证:.
17.如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.
18.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.
19.如图,G
为
BC
的中点,且
DG⊥BC,DE⊥AB
于
E,DF⊥AC
于
F,
BE=CF.
(1)求证:AD
是∠BAC
的平分线;
(2)如果
AB=8,AC=6,求
AE
的长.
20.如图,中,,D,E,F分别为AB,BC,CA上的点,且,.
(1)求证:≌;
(2)若,求的度数.
21.如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.
22.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,
CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
试卷第1页,总3页
参考答案
1.C2.C3.C4.A5.A6.B7.B8.B9.D10.D
11.OB=OD(或AO=CO或AB=CD)
12.60°
13.ABC,
DCB,
HL,
AOB,
DOC,
AAS.
14.3
15.4
18.(2).
19.(2)7.
20.(2)55°.
21.(1)四边形ACGD为平行四边形
22.(2)成立(3)△DEF为等边三角形
