沪科版2020-2021学年九年级上数学期末模拟卷(Word版 含答案)
文档属性
| 名称 | 沪科版2020-2021学年九年级上数学期末模拟卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 667.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:42:05 | ||
图片预览



文档简介
沪科版2020-2021学年九年级上数学期末模拟卷
一、单项选择题(本大题共10小题,每小题4分,共40分)
1.在下列四个图形中,是中心对称图形的是(
)
A.
B.
C.
D.
2.下列计算错误的个数是(
)
①②③;④
A.1个
B.2个
C.3个
D.4个
3.若反比例函数的图像位于第二、四象限,则的取值可以是(
)
A.0
B.1
C.2
D.以上都不是
4.如图,在网格中,小正方形的边长均为1,点、、都在格点上,则的正切值是(
)
A.2
B.
C.
D.
5.点是的外心,若,则的度数为(
)
A.
B.
C.或
D.或
6.如图,圆弧形桥拱的跨度米,拱高米,则拱桥的半径为(
)
A.6.5米
B.9米
C.13米
D.15米
7.已知二次函数的图象与轴有两个交点,则的取值范围是(
)
A.
B.
C.且
D.
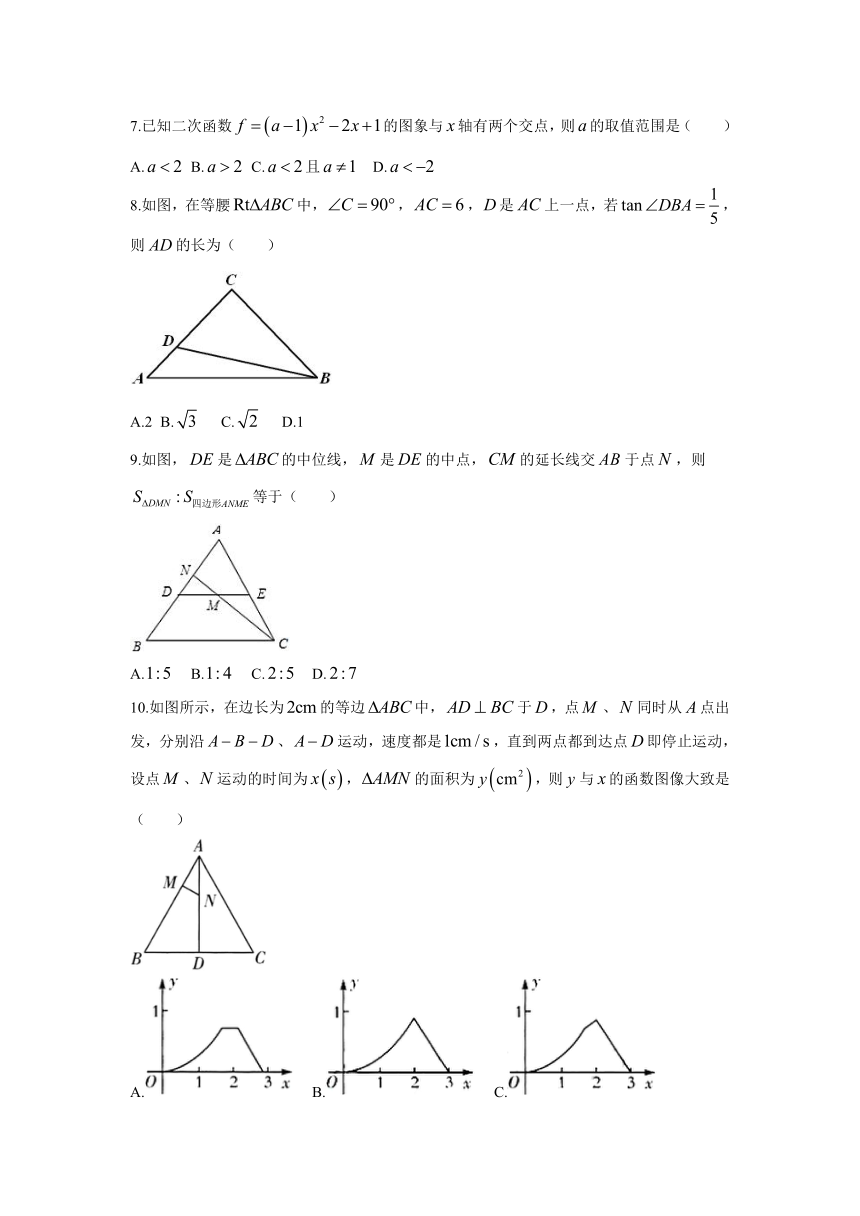
8.如图,在等腰中,,,是上一点,若,则的长为(
)
A.2
B.
C.
D.1
9.如图,是的中位线,是的中点,的延长线交于点,则等于(
)
A.
B.
C.
D.
10.如图所示,在边长为的等边中,于,点、同时从点出发,分别沿、运动,速度都是,直到两点都到达点即停止运动,设点、运动的时间为,的面积为,则与的函数图像大致是(
)
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.如图,为的弦,半径交于点,,,,则长为______
12.在中,,则的大小是______
13.二次函数图像上部分点的对应值如下表:
-3
-2
-1
0
1
2
3
4
6
0
-4
-6
-6
-4
0
6
则使的的取值范围为______
14.在中,,,,点、分别在、上,连接,将沿折叠,使点落在边上的点处,若有一边垂直,则______
三、解答题(本大题共9题,其中第15、16、17、18题每题8分;第19、20题每题10分;第21、22题每题12分;第23题14分)
15.计算:
16.在边长为1的小正方形组成的网格中建立如图所示的平面直角坐标系,为格点三角形(顶点是网格线的交点).
(1)画出以点为旋转中心,顺时针旋转得到的;
(2)以点为位似中心,在第一象限画出的位似图形,使与的位似比为.
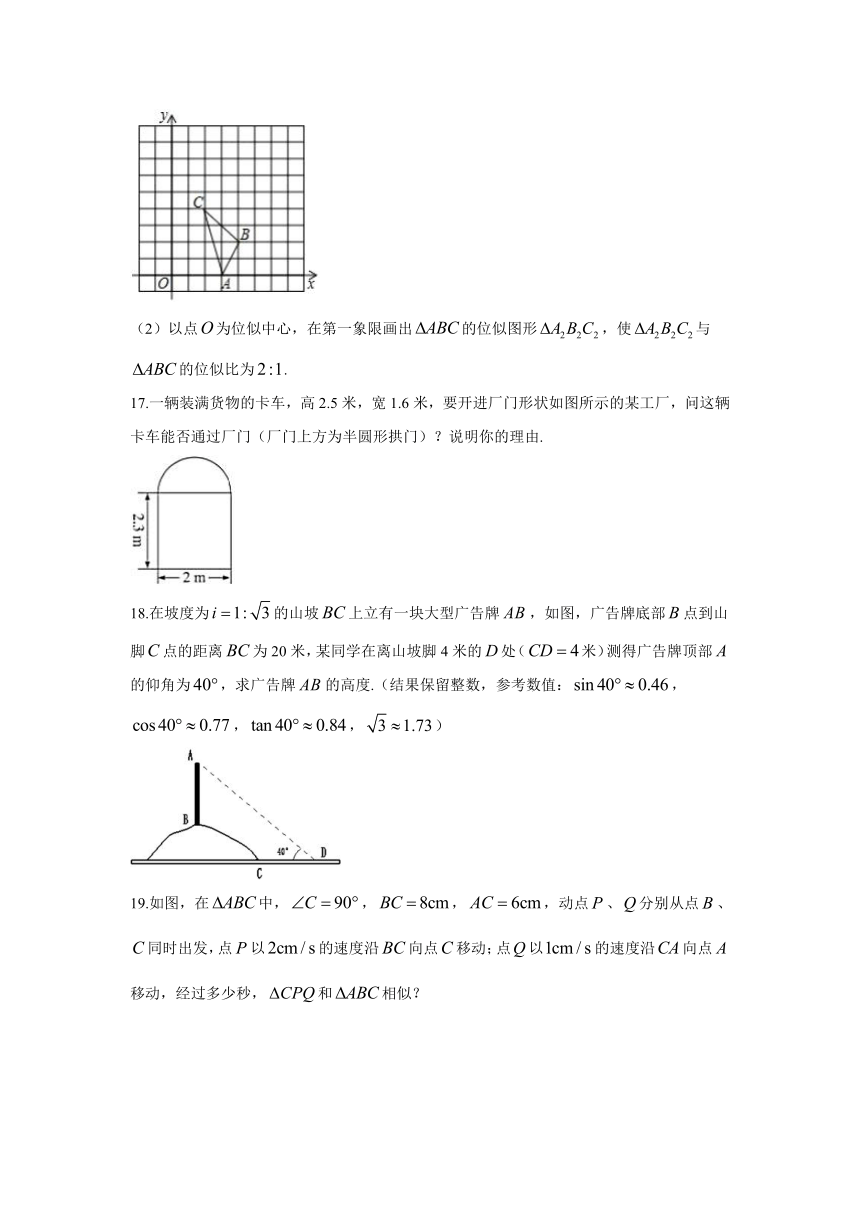
17.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
18.在坡度为的山坡上立有一块大型广告牌,如图,广告牌底部点到山脚点的距离为20米,某同学在离山坡脚4米的处(米)测得广告牌顶部的仰角为,求广告牌的高度.(结果保留整数,参考数值:,,,)
19.如图,在中,,,,动点、分别从点、同时出发,点以的速度沿向点移动;点以的速度沿向点移动,经过多少秒,和相似?
20.如图,反比例函数与一次函数的图像交于点、.
(1)求这两个函数解析式;
(2)将一次函数的图像沿轴向下平移个单位,使平移后的图像与反比例函数的图像有且只有一个交点,求的值.
21.如图,是的外接圆,是弦的中点,是外一点且,连接并延长交于点,交于点.
(1)求证:是的切线
(2)若的半径为6,求弦的长.
22.在平面直角坐标系中,抛物线;
(1)当抛物线的顶点在轴上时,求该抛物线的解析式;
(2)不论取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
(3)若有两点,,且该抛物线与线段始终有交点,请直接写出的取值范围.
23.已知,如图,和都是等腰直角三角形,,的顶点与的斜边的中点重合,将绕点旋转,线段与线段相交于点,射线与射线相交于点.
(1)求证:
(2)求证:平分
(3)当,时,求的长.
参考答案
一、选择题(本题共10小题,每题4分,共40分,每小题有四个答案,其中有且只有一个答案是正确的)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
A
D
C
A
C
A
A
C
填空题(本大题共4小题,每小题5分,满分20分)
11、8
12、120°
13、-2<x<3
14
、或
解析:分两种情况:(1)如图1当D点与C点重合,即ED⊥BC时,EF=
(2)如图2
当FD⊥BC时,设AE=x,则ED=x,CE=4-x,易得四边形AEDF是菱形,∴ED//AB
∴?CDE∽?CBA
∴
==,
∴==
∴x=,CD=
∴AD==
∵S菱形AEDF=CD·AE=AD·EF
∴EF=
,综上,EF长为或
解答题(本大题共9题,其中15、16、17、18题每题8分,第19、20题每题10分,第21、22题每题12分,第23题14分)
15、计算:∣1-∣+
2cos45°–
+()-1
=-1+2×-+3
(4分)
=2
(8分)
16、(1)如图所示
(4分)
(2)如图所示
(8分)
17、解:这辆卡车能通过厂门。
如图M、N为卡车的宽度,过M、N作AB的垂线交半圆
与C、D,过O作OE⊥CD,E为垂足,则CD=MN=1.6m,
AB=2m,由做法得,CE=DE=0.8m,
又∵OC=OA=1m,在Rt?OCE中,
OE===0.6(m),
(6分)
∴CM=2.3+0.6=2.9m>2.5m,所以这辆卡车能通过厂门。(8分)
18、解:延长AB交CE于点E,在Rt?BCE中,∠CEB=90°,
∵tan∠BCE=
i
=1:,∴∠BCE=30°,∴BE=BC=10米,
由勾股定理的CE==10≈17.3米
(3分)
在Rt?ADE中,∠AED=90°,
∵DE=CE+CD≈21.3,
tan40°=,
∴AE≈21.3×0.84≈17.9米
(6分)
∴AB=AE-BE≈17.9-10≈8(米)
答:广告牌AB的高度约为8米。
(8分)
19、解:设经过t秒,则BP=2t,CQ=t,
∴PC=8-2t,
∵∠QCP=∠ACB,
∴当
=时,即
=,解得t=2.4
(5分)
当=时,即
=,解得t=
综上,经过2.4或秒
(10分)
20、解:(1)把(2,2)代入y=
中,解得k=4,∴反比例函数解析式为y=
,将A(2,2)
B(,8)
代入y=ax+b中,解得a=
-4
,
b=10。
∴一次函数解析式为y=-4x+10
(5分)
(2)将直线y=-4x+10向下平移m个单位得直线y=-4x+10-m,联立
,-4x+10-m=
∴4x2+(m-10)x+4=0,由题意得?=(m-10)2-64=0,解得m=2或18
(10分)
21、(1)证明:如图,连接OB
∵E是弦BC的中点,
(1分)
∴BE=CE,OE⊥BC,
==
(2分)
∴∠BOE=∠A,
∠OBE+∠BOE=90°
(3分)
∵∠PBC=∠A,
∴∠BOE=∠PBC
∴∠OBE+∠PBC=90°即BP⊥OB
(5分)
∴BP是⊙O的切线
(6分)
(2)解:∵OB=6,BD=8,BD⊥OB
∴OD==10
(8分)
∵?OBD的面积=OD·BE=OB·BD,
∴BE===4.8
(10分)
∴BC=2BE=9.6
(12分)
22、解:∵,
∴顶点坐标是,
∵抛物线的顶点在轴上,
∴,
∴,
∴;
(4分)
∵抛物线的顶点坐标是,
∴抛物线的顶点在直线上;
(8分)
当抛物线过点时,
,
解得,,
当抛物线过点时,
,
解得,,
故.
(12分)
23、∵?ABC和?DEF都是等腰直角三角形,
∴∠A=∠B=∠DEF=45°而∠PEB+∠AEQ=∠PEB+∠EPB=180°-45°=135°
∴∠AEQ=∠BPE
∴?AEQ∽?BPE
(4分)
(2)∵?AEQ∽?BPE
∴∠AEQ=∠BPE,
=,而AE=BE,
∴=
∵∠A=∠DEF=45°
∴?AEQ∽?EPQ
∴∠AEQ=∠EPQ
∴∠EPQ=∠BPE,即PE平分∠BPQ
(8分)
(3)∵AE=BE=3,∠ACB=90°,AC=BC,易得AC=BC=6,
∵∠B=45°,BE=3,EH⊥BC
又∵?AEQ∽?BPE
∴=
∴BP===9
∴CP=BP-BC=9-6=3
∴CQ=AC-AQ=6-2=4
∴PQ==5
(14分)
一、单项选择题(本大题共10小题,每小题4分,共40分)
1.在下列四个图形中,是中心对称图形的是(
)
A.
B.
C.
D.
2.下列计算错误的个数是(
)
①②③;④
A.1个
B.2个
C.3个
D.4个
3.若反比例函数的图像位于第二、四象限,则的取值可以是(
)
A.0
B.1
C.2
D.以上都不是
4.如图,在网格中,小正方形的边长均为1,点、、都在格点上,则的正切值是(
)
A.2
B.
C.
D.
5.点是的外心,若,则的度数为(
)
A.
B.
C.或
D.或
6.如图,圆弧形桥拱的跨度米,拱高米,则拱桥的半径为(
)
A.6.5米
B.9米
C.13米
D.15米
7.已知二次函数的图象与轴有两个交点,则的取值范围是(
)
A.
B.
C.且
D.
8.如图,在等腰中,,,是上一点,若,则的长为(
)
A.2
B.
C.
D.1
9.如图,是的中位线,是的中点,的延长线交于点,则等于(
)
A.
B.
C.
D.
10.如图所示,在边长为的等边中,于,点、同时从点出发,分别沿、运动,速度都是,直到两点都到达点即停止运动,设点、运动的时间为,的面积为,则与的函数图像大致是(
)
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.如图,为的弦,半径交于点,,,,则长为______
12.在中,,则的大小是______
13.二次函数图像上部分点的对应值如下表:
-3
-2
-1
0
1
2
3
4
6
0
-4
-6
-6
-4
0
6
则使的的取值范围为______
14.在中,,,,点、分别在、上,连接,将沿折叠,使点落在边上的点处,若有一边垂直,则______
三、解答题(本大题共9题,其中第15、16、17、18题每题8分;第19、20题每题10分;第21、22题每题12分;第23题14分)
15.计算:
16.在边长为1的小正方形组成的网格中建立如图所示的平面直角坐标系,为格点三角形(顶点是网格线的交点).
(1)画出以点为旋转中心,顺时针旋转得到的;
(2)以点为位似中心,在第一象限画出的位似图形,使与的位似比为.
17.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
18.在坡度为的山坡上立有一块大型广告牌,如图,广告牌底部点到山脚点的距离为20米,某同学在离山坡脚4米的处(米)测得广告牌顶部的仰角为,求广告牌的高度.(结果保留整数,参考数值:,,,)
19.如图,在中,,,,动点、分别从点、同时出发,点以的速度沿向点移动;点以的速度沿向点移动,经过多少秒,和相似?
20.如图,反比例函数与一次函数的图像交于点、.
(1)求这两个函数解析式;
(2)将一次函数的图像沿轴向下平移个单位,使平移后的图像与反比例函数的图像有且只有一个交点,求的值.
21.如图,是的外接圆,是弦的中点,是外一点且,连接并延长交于点,交于点.
(1)求证:是的切线
(2)若的半径为6,求弦的长.
22.在平面直角坐标系中,抛物线;
(1)当抛物线的顶点在轴上时,求该抛物线的解析式;
(2)不论取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
(3)若有两点,,且该抛物线与线段始终有交点,请直接写出的取值范围.
23.已知,如图,和都是等腰直角三角形,,的顶点与的斜边的中点重合,将绕点旋转,线段与线段相交于点,射线与射线相交于点.
(1)求证:
(2)求证:平分
(3)当,时,求的长.
参考答案
一、选择题(本题共10小题,每题4分,共40分,每小题有四个答案,其中有且只有一个答案是正确的)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
A
D
C
A
C
A
A
C
填空题(本大题共4小题,每小题5分,满分20分)
11、8
12、120°
13、-2<x<3
14
、或
解析:分两种情况:(1)如图1当D点与C点重合,即ED⊥BC时,EF=
(2)如图2
当FD⊥BC时,设AE=x,则ED=x,CE=4-x,易得四边形AEDF是菱形,∴ED//AB
∴?CDE∽?CBA
∴
==,
∴==
∴x=,CD=
∴AD==
∵S菱形AEDF=CD·AE=AD·EF
∴EF=
,综上,EF长为或
解答题(本大题共9题,其中15、16、17、18题每题8分,第19、20题每题10分,第21、22题每题12分,第23题14分)
15、计算:∣1-∣+
2cos45°–
+()-1
=-1+2×-+3
(4分)
=2
(8分)
16、(1)如图所示
(4分)
(2)如图所示
(8分)
17、解:这辆卡车能通过厂门。
如图M、N为卡车的宽度,过M、N作AB的垂线交半圆
与C、D,过O作OE⊥CD,E为垂足,则CD=MN=1.6m,
AB=2m,由做法得,CE=DE=0.8m,
又∵OC=OA=1m,在Rt?OCE中,
OE===0.6(m),
(6分)
∴CM=2.3+0.6=2.9m>2.5m,所以这辆卡车能通过厂门。(8分)
18、解:延长AB交CE于点E,在Rt?BCE中,∠CEB=90°,
∵tan∠BCE=
i
=1:,∴∠BCE=30°,∴BE=BC=10米,
由勾股定理的CE==10≈17.3米
(3分)
在Rt?ADE中,∠AED=90°,
∵DE=CE+CD≈21.3,
tan40°=,
∴AE≈21.3×0.84≈17.9米
(6分)
∴AB=AE-BE≈17.9-10≈8(米)
答:广告牌AB的高度约为8米。
(8分)
19、解:设经过t秒,则BP=2t,CQ=t,
∴PC=8-2t,
∵∠QCP=∠ACB,
∴当
=时,即
=,解得t=2.4
(5分)
当=时,即
=,解得t=
综上,经过2.4或秒
(10分)
20、解:(1)把(2,2)代入y=
中,解得k=4,∴反比例函数解析式为y=
,将A(2,2)
B(,8)
代入y=ax+b中,解得a=
-4
,
b=10。
∴一次函数解析式为y=-4x+10
(5分)
(2)将直线y=-4x+10向下平移m个单位得直线y=-4x+10-m,联立
,-4x+10-m=
∴4x2+(m-10)x+4=0,由题意得?=(m-10)2-64=0,解得m=2或18
(10分)
21、(1)证明:如图,连接OB
∵E是弦BC的中点,
(1分)
∴BE=CE,OE⊥BC,
==
(2分)
∴∠BOE=∠A,
∠OBE+∠BOE=90°
(3分)
∵∠PBC=∠A,
∴∠BOE=∠PBC
∴∠OBE+∠PBC=90°即BP⊥OB
(5分)
∴BP是⊙O的切线
(6分)
(2)解:∵OB=6,BD=8,BD⊥OB
∴OD==10
(8分)
∵?OBD的面积=OD·BE=OB·BD,
∴BE===4.8
(10分)
∴BC=2BE=9.6
(12分)
22、解:∵,
∴顶点坐标是,
∵抛物线的顶点在轴上,
∴,
∴,
∴;
(4分)
∵抛物线的顶点坐标是,
∴抛物线的顶点在直线上;
(8分)
当抛物线过点时,
,
解得,,
当抛物线过点时,
,
解得,,
故.
(12分)
23、∵?ABC和?DEF都是等腰直角三角形,
∴∠A=∠B=∠DEF=45°而∠PEB+∠AEQ=∠PEB+∠EPB=180°-45°=135°
∴∠AEQ=∠BPE
∴?AEQ∽?BPE
(4分)
(2)∵?AEQ∽?BPE
∴∠AEQ=∠BPE,
=,而AE=BE,
∴=
∵∠A=∠DEF=45°
∴?AEQ∽?EPQ
∴∠AEQ=∠EPQ
∴∠EPQ=∠BPE,即PE平分∠BPQ
(8分)
(3)∵AE=BE=3,∠ACB=90°,AC=BC,易得AC=BC=6,
∵∠B=45°,BE=3,EH⊥BC
又∵?AEQ∽?BPE
∴=
∴BP===9
∴CP=BP-BC=9-6=3
∴CQ=AC-AQ=6-2=4
∴PQ==5
(14分)
同课章节目录
