沪教版(上海)初中数学九年级第一学期 25.1 锐角三角比的意义 课件
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 25.1 锐角三角比的意义 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 816.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:36:39 | ||
图片预览






文档简介
(共23张PPT)
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c
、a、b
.
tanA=
cotA=
sinA=
cosA=
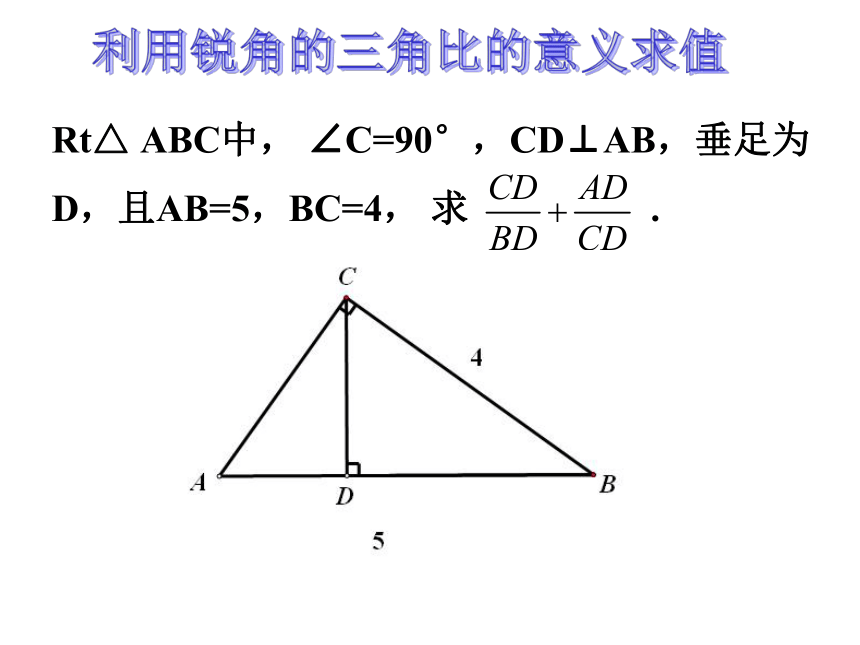
Rt△
ABC中,
∠C=90°,CD⊥AB,垂足为D,且AB=5,BC=4,
求
.
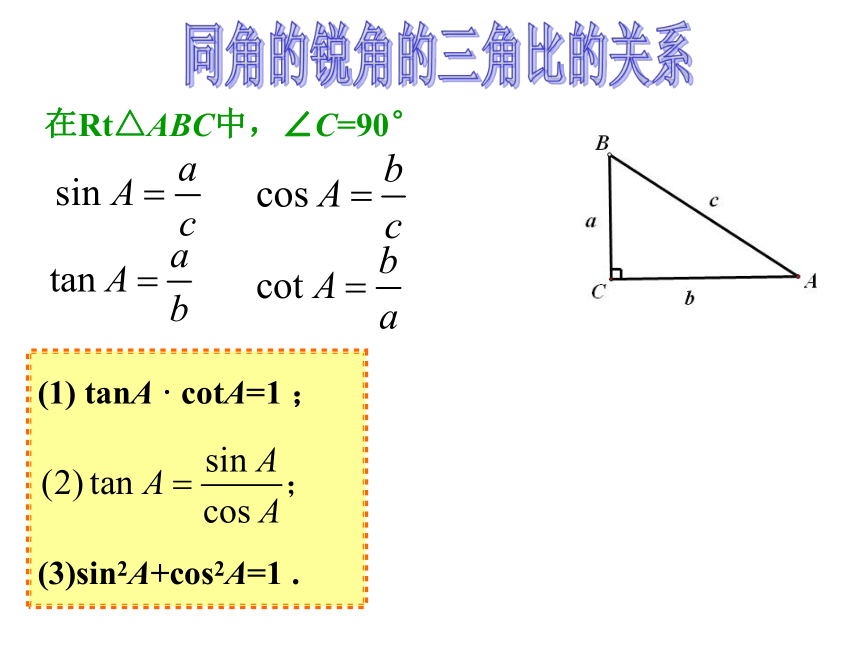
在Rt△ABC中,∠C=90°
(1)
tanA
·
cotA=1
;
(3)sin2A+cos2A=1
.
若∠A+∠B=90
°,则
(1)sinA=cosB,cosA=sinB;
(2)tanA=cotB,cotA=tanB.
在Rt△ABC中,∠C=90°,∠A+∠B=90
°
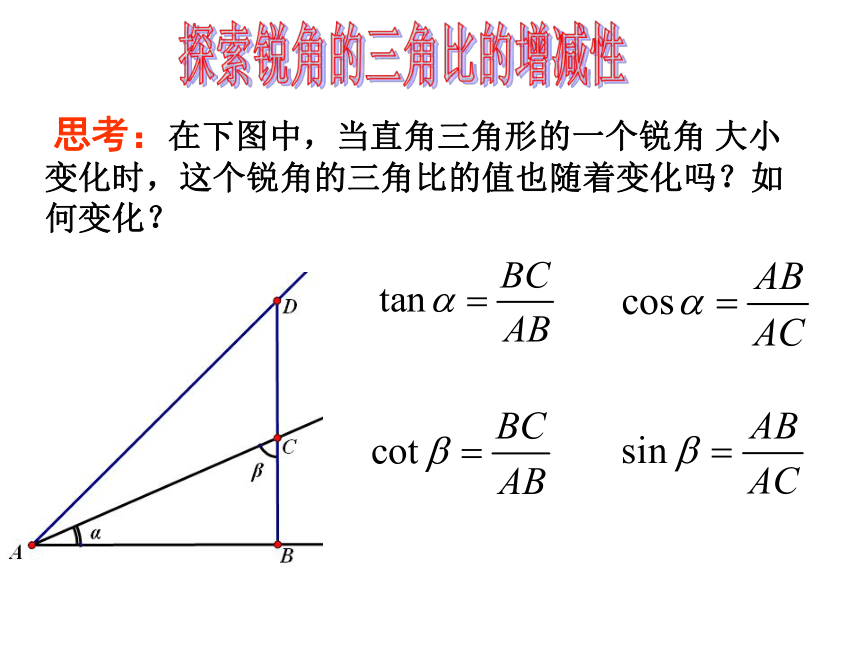
思考:在下图中,当直角三角形的一个锐角
大小变化时,这个锐角的三角比的值也随着变化吗?如何变化?
当0<α<90
°时,
sinα和tan
α的值随α的增大而增大;
cos
α和cot
α的值随α的增大而减小.
1.已知∠A,∠B为锐角
(1)若∠A<∠B,则tanA
tanB;
(2)若tanA∠B;
(3)若∠A<∠B,则sinA
sinB;
(4)若cosA∠B.
<
<
<
>
2.比较大小:
sin47
°
sin48
°
;
cos30
°
sin60
°
;
cos43
°
sin43
°.
<
=
>
0<sin
A<1;0<cos
A<1;
tanA>0;
cotA>0.
在Rt△ABC中,∠C=90°
.
1.
在直角坐标平面中有一点
P(3,4),求OP与x轴正半轴的夹角α的正切、正弦、和余弦的值.
∴tanα=
sinα=
cosα
=
解:作PQ⊥x轴于点Q,
则OQ=3,QP=4.
在Rt△OPQ中,
OP=
Q
2.
已知cosα=
,且α是锐角,
求sinα,tanα,cotα的值.
3.在等腰△ABC中,AB=AC=13,BC=10,求tanB.
说明:作高是构造直角三角形的重要手段.
思考tan∠BAC=
?
4.在等腰△ABC中,AB=AC,且AB=2BC,求tan∠BAC.
tan∠EBC
5.
如图,在△ABC中,∠C=90°,CD⊥AB于D,
已知BC=12,AC=5,求∠DCB的四个三角比.
?
说明:求一个锐角的三角比的值,常常转化为求与它相等的角的三角比的值.
6.如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
.
求:(1)线段CD的长;
(2)tan∠EDC的值.
7.在梯形ABCD中,AB//CD,DA⊥AB,AB
=4,CD=3,AD=7.
(1)求cosB的值.
(2)若点E在AD上移动,当BE⊥EC
,求tan∠DCE.
(3)如果点E
在AD上移动,△BEC为
直角三角形,求tan∠DCE的值.
8.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=
.
(1)求线段CD的长;
(2)求sin∠DBE的值.
F
一个锐角的正弦、余弦、正切、余切
统称为这个锐角的三角比.
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c
、a、b
.
特别关注:一个锐角的三角比只与这个锐角
的大小有关而与直角三角形的边长无关.
.
1.同一个角的锐角三角比的关系:
(1)sin2A+cos2A=1;
(2)tanA
·
cotA=1;
2.互余两锐角的三角比之间的关系:
若∠A+∠B=90
°
,则
(1)sinA=cosB,cosA=sinB;
(2)tanA=cotB,cotA=tanB.
3.
锐角三角比的增减性:
当0<α<90
°时,
sinα和tan
α的值随α的增大而增大;
cos
α和cot
α的值随α的增大而减小.
4.锐角三角比的取值范围:
0<sin
A<1;0<cos
A<1;
tanA>0;
cotA>0.
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c
、a、b
.
tanA=
cotA=
sinA=
cosA=
Rt△
ABC中,
∠C=90°,CD⊥AB,垂足为D,且AB=5,BC=4,
求
.
在Rt△ABC中,∠C=90°
(1)
tanA
·
cotA=1
;
(3)sin2A+cos2A=1
.
若∠A+∠B=90
°,则
(1)sinA=cosB,cosA=sinB;
(2)tanA=cotB,cotA=tanB.
在Rt△ABC中,∠C=90°,∠A+∠B=90
°
思考:在下图中,当直角三角形的一个锐角
大小变化时,这个锐角的三角比的值也随着变化吗?如何变化?
当0<α<90
°时,
sinα和tan
α的值随α的增大而增大;
cos
α和cot
α的值随α的增大而减小.
1.已知∠A,∠B为锐角
(1)若∠A<∠B,则tanA
tanB;
(2)若tanA
(3)若∠A<∠B,则sinA
sinB;
(4)若cosA
<
<
<
>
2.比较大小:
sin47
°
sin48
°
;
cos30
°
sin60
°
;
cos43
°
sin43
°.
<
=
>
0<sin
A<1;0<cos
A<1;
tanA>0;
cotA>0.
在Rt△ABC中,∠C=90°
.
1.
在直角坐标平面中有一点
P(3,4),求OP与x轴正半轴的夹角α的正切、正弦、和余弦的值.
∴tanα=
sinα=
cosα
=
解:作PQ⊥x轴于点Q,
则OQ=3,QP=4.
在Rt△OPQ中,
OP=
Q
2.
已知cosα=
,且α是锐角,
求sinα,tanα,cotα的值.
3.在等腰△ABC中,AB=AC=13,BC=10,求tanB.
说明:作高是构造直角三角形的重要手段.
思考tan∠BAC=
?
4.在等腰△ABC中,AB=AC,且AB=2BC,求tan∠BAC.
tan∠EBC
5.
如图,在△ABC中,∠C=90°,CD⊥AB于D,
已知BC=12,AC=5,求∠DCB的四个三角比.
?
说明:求一个锐角的三角比的值,常常转化为求与它相等的角的三角比的值.
6.如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
.
求:(1)线段CD的长;
(2)tan∠EDC的值.
7.在梯形ABCD中,AB//CD,DA⊥AB,AB
=4,CD=3,AD=7.
(1)求cosB的值.
(2)若点E在AD上移动,当BE⊥EC
,求tan∠DCE.
(3)如果点E
在AD上移动,△BEC为
直角三角形,求tan∠DCE的值.
8.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=
.
(1)求线段CD的长;
(2)求sin∠DBE的值.
F
一个锐角的正弦、余弦、正切、余切
统称为这个锐角的三角比.
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c
、a、b
.
特别关注:一个锐角的三角比只与这个锐角
的大小有关而与直角三角形的边长无关.
.
1.同一个角的锐角三角比的关系:
(1)sin2A+cos2A=1;
(2)tanA
·
cotA=1;
2.互余两锐角的三角比之间的关系:
若∠A+∠B=90
°
,则
(1)sinA=cosB,cosA=sinB;
(2)tanA=cotB,cotA=tanB.
3.
锐角三角比的增减性:
当0<α<90
°时,
sinα和tan
α的值随α的增大而增大;
cos
α和cot
α的值随α的增大而减小.
4.锐角三角比的取值范围:
0<sin
A<1;0<cos
A<1;
tanA>0;
cotA>0.
